2022-2023学年山东省济南市钢城区八年级（下）期末数学试卷（五四学制）（含解析）

这是一份2022-2023学年山东省济南市钢城区八年级（下）期末数学试卷（五四学制）（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 9化简的结果是( )
A. −3B. 3C. ±3D. 3
2. 图1是伸缩折叠不锈钢晾衣架的实物图，图2是它的侧面示意图，AD与CB相交于点O，AB//CD，根据图2中的数据可得x的值为( )
A. 0.8B. 0.96C. 1D. 1.08
3. 下列计算中，正确的是( )
A. 4+ 9= 13B. 27÷ 3=9
C. 5× 2= 10D. 3 2− 2=3
4. 如图，△ADE∽△ACB，DE=5，S△ADE：S四边形BCED=9：16，则BC为( )
A. 8
B. 203
C. 253
D. 10
5. 一元二次方程x2+x+1=0 的根的情况为( )
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 只有一个实数根D. 没有实数根
6. 某商店将一批夏装降价处理，经过两次降价后，由每件100元降至81元，求平均每次降价的百分率.设平均每次降价的百分率为x，可列方程( )
A. 100(1−x)2=81B. 81(1+x)2=100
C. 100(1+x)=81×2D. 2×100(1−x)=8
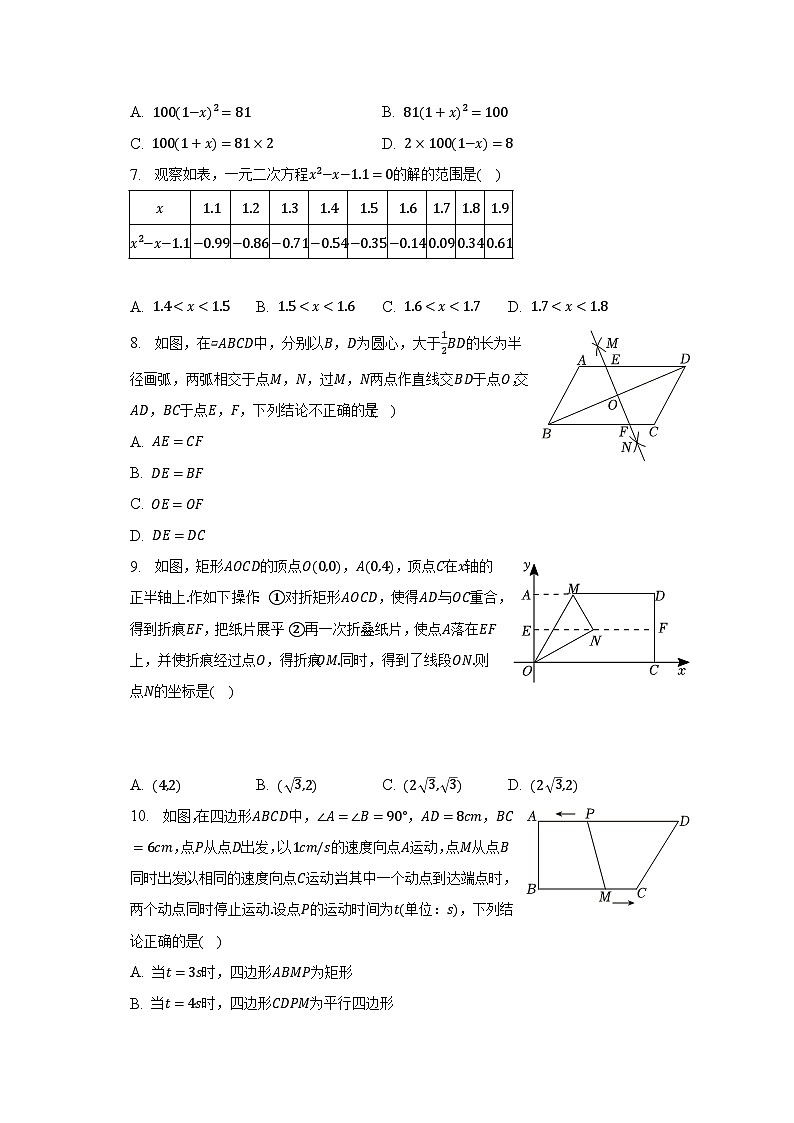
7. 观察如表，一元二次方程x2−x−1.1=0的解的范围是( )
A. 1.48. 如图，在▱ABCD中，分别以B，D为圆心，大于12BD的长为半径画弧，两弧相交于点M，N，过M，N两点作直线交BD于点O，交AD，BC于点E，F，下列结论不正确的是( )
A. AE=CF
B. DE=BF
C. OE=OF
D. DE=DC
9. 如图，矩形AOCD的顶点O(0,0)，A(0,4)，顶点C在x轴的正半轴上.作如下操作：①对折矩形AOCD，使得AD与OC重合，得到折痕EF，把纸片展平；②再一次折叠纸片，使点A落在EF上，并使折痕经过点O，得折痕OM.同时，得到了线段ON.则点N的坐标是( )
A. (4,2)B. ( 3,2)C. (2 3, 3)D. (2 3,2)
10. 如图，在四边形ABCD中，∠A=∠B=90°，AD=8cm，BC=6cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动.设点P的运动时间为t(单位：s)，下列结论正确的是( )
A. 当t=3s时，四边形ABMP为矩形
B. 当t=4s时，四边形CDPM为平行四边形
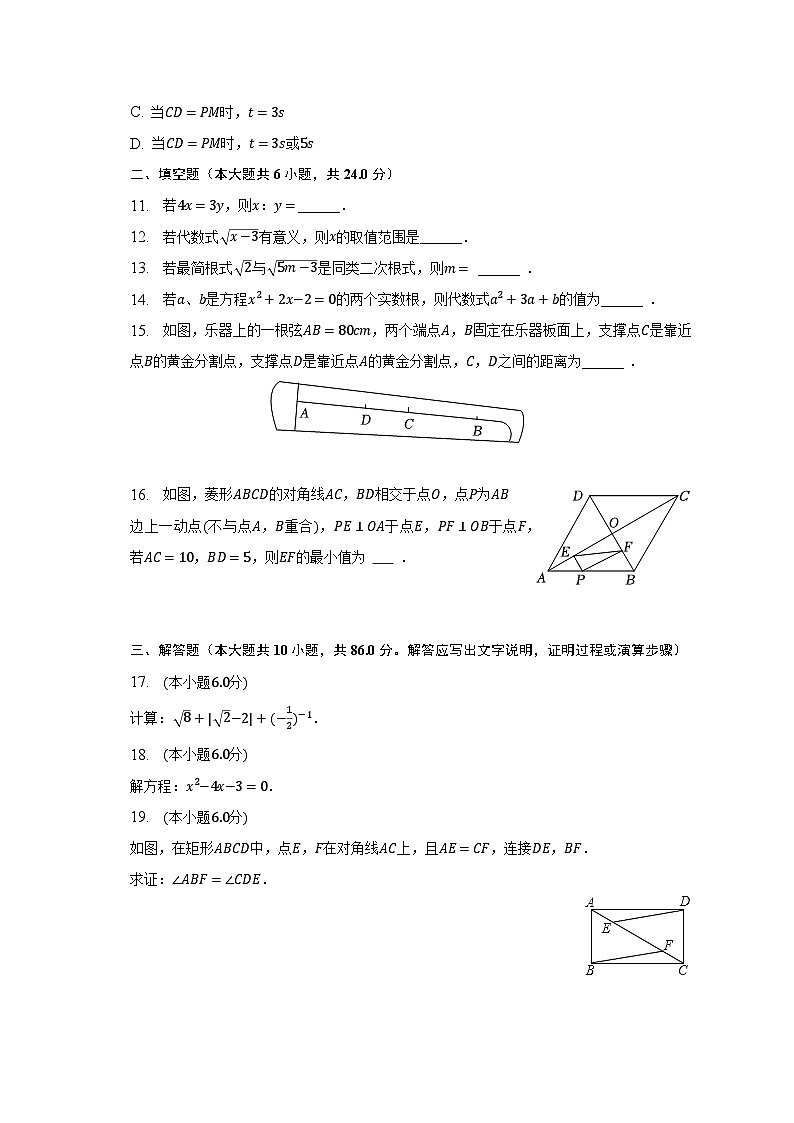
C. 当CD=PM时，t=3s
D. 当CD=PM时，t=3s或5s
二、填空题（本大题共6小题，共24.0分）
11. 若4x=3y，则x：y=______．
12. 若代数式 x−3有意义，则x的取值范围是______．
13. 若最简根式 2与 5m−3是同类二次根式，则m= ______ ．
14. 若a、b是方程x2+2x−2=0的两个实数根，则代数式a2+3a+b的值为______ ．
15. 如图，乐器上的一根弦AB=80cm，两个端点A，B固定在乐器板面上，支撑点C是靠近点B的黄金分割点，支撑点D是靠近点A的黄金分割点，C，D之间的距离为______ ．
16. 如图，菱形ABCD的对角线AC，BD相交于点O，点P为AB边上一动点(不与点A，B重合)，PE⊥OA于点E，PF⊥OB于点F，若AC=10，BD=5，则EF的最小值为 ．
三、解答题（本大题共10小题，共86.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
计算： 8+| 2−2|+(−12)−1．
18. (本小题6.0分)
解方程：x2−4x−3=0．
19. (本小题6.0分)
如图，在矩形ABCD中，点E，F在对角线AC上，且AE=CF，连接DE，BF．
求证：∠ABF=∠CDE．
20. (本小题8.0分)
在平面直角坐标系内，△ABC的位置如图所示．
(1)将△ABC绕点O顺时针旋转90°得到△A1B1C1，作出△A1B1C1．
(2)以原点O为位似中心，在第四象限内作出△ABC的位似图形△A2B2C2，且△A2B2C2与△ABC的相似比为2：1．
21. (本小题8.0分)
如图，已知等腰△ABC，AB=AC，点D、E分别在BC、AB上，且∠BDE=∠CAD．
(1)求证：△BDE∽△CAD；
(2)如果BE=3，BD=4，DC=9，求AB的长．
22. (本小题8.0分)
一款服装每件进价为80元，销售价为120元时，每天可售出20件.经市场调查发现，如果每件服装降价1元，那么平均每天可多售出2件．
(1)设每件服装降价x元，则每天销售量增加______ 件，每件服装盈利______ 元(用含x的代数式表示)；
(2)在让利于顾客的情况下，每件服装降价多少元时，商家平均每天能盈利1200元？
23. (本小题10.0分)
如图，已知△ABC和△ADE，AB=AC，AD=AE，点D在BC边上，∠BAD=∠CAE，边DE与AC相交于点F．
(1)求证：△ABC∽△ADE；
(2)如果AE//BC，DA=DC，连结CE．
求证：四边形ADCE是菱形．
24. (本小题10.0分)
在解决问题“已知a=12+ 3，求2a2−8a+1的值”时，小明是这样分析与解答的：
因为a=12+ 3=2− 3(2+ 3)(2− 3)=2− 3
所以a−2=− 3，所以(a−2)2=3，a2−4a+4=3
所以a2−4a=−1，所以2a2−8a+1=2(a2−4a)+1=2×(−1)+1=−1．
请你根据小明的分析过程，解决如下问题：
(1)化简：3 5− 2；
(2)若a=1 2+1，求2a2+4a−1的值．
25. (本小题12.0分)
如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm点P从A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动.点P，Q同时出发，当点Q运动到点C时，两点停止运动，设运动时间为t秒．
(1)填空：BQ= ______ cm，PB= ______ cm；(用含t的代数式表示)
(2)当t为几秒时，PQ的长度等于4 2．
(3)是否存在某一时刻t，使四边形APQC的面积等于△ABC面积的23？如果存在，求出t的值，如果不存在，请说明理由，
26. (本小题12.0分)
原题再现：小百合特别喜欢探究数学问题，一天万老师给她这样一个几何问题：
△ABC和△BDE都是等边三角形，将△BDE绕着点B旋转到图1位置，求证：AE=CD.小百合很快就通过△ABE≌△CBD，论证了AE=CD．
(1)请你帮助小百合写出证明过程；
迁移应用：小百合想，把等边△ABC和等边△BDE都换成等腰直角三角形，将△BDE绕着点B旋转到图2位置，其中∠ACB=∠EDB=90°，那么AE和CD有什么数量关系呢？
(2)请你帮助小百合写出结论，并给出证明；
(3)如图3，如果把等腰直角三角形换成正方形，将正方形AFEG绕点A旋转α°，若AB=6 2，AG=4，在旋转过程中，当C，G，E三点共线时，请直接写出DG的长度．
答案和解析
1.【答案】B
【解析】解： 9=3，
故选：B．
根据二次根式的性质求出即可．
本题考查了二次根式的性质的应用，主要考查学生的计算能力，题目比较好，难度不大．
2.【答案】B
【解析】解：∵AB//CD，
∴△COD∽△BOA，
∴CDAB=x1.2，
∴0.81=x1.2，
∴x=0.96，
故选：B．
由AB//CD，可得出△COD∽△BOA，进而得出0.81=x1.2，解出即可得出结论．
本题主要考查了三角形相似的判定和性质，熟练掌握相似的判定和性质是解此题的关键．
3.【答案】C
【解析】解：A． 4+ 9=2+3=5，故计算错误，不符合题意；
B. 27÷ 3= 9=3，故计算错误，不符合题意；
C. 5× 2= 10，故计算错误，符合题意；
D.3 2− 2=2 2，故计算错误，不符合题意；
故选：C．
根据算术平方根的含义可判断A；
根据二次根式的除法运算可判断B；
根据二次根式的乘法运算可判断C；
根据二次根式的减法运算可判断D．
本题考查了算术平方根的含义，二次根式的加减乘除运算，掌握相应的运算法则是解本题的关键．
4.【答案】C
【解析】解：∵S△ADE：S四边形BCED=9：16，
∴S△ADE：S△ACB=9：25，
∴相似比为k=3：5，即DEBC=35，5BC=35，
∴BC=253；
故选：C．
根据S△ADE：S四边形BCED的比，可得S△ADE：S△ACB的比，利用面积比是相似比的平方，可得DEBC，从而可得答案．
本题考查了形似三角形的性质，解题的关键是掌握面积比是相似比的平方．
5.【答案】D
【解析】解：x2+x+1=0，
∵△=12−4=−3<0，
∴一元二次方程x2+x+1=0没有实数根，
故选D．
本题考查根的判别式，解题的关键是由根的判别式的正负判断一元二次方程根的情况．
6.【答案】A
【解析】解：设平均每次降价的百分率为x，根据题意列方程得：
100(1−x)2=81，
故选：A．
此题可设平均每次降价的百分率为x，那么第一次降价后的单价是原来的(1−x)，那么第二次降价后的单价是原来的(1−x)2，根据题意列方程解答即可．
本题考查的是平均变化率问题．解决这类问题所用的等量关系一般是：a(1±x)2=b．
7.【答案】C
【解析】
【分析】
本题考查了估算一元二次方程的近似解：用列举法估算一元二次方程的近似解，具体方法是：给出一些未知数的值，计算方程两边结果，当两边结果愈接近时，说明未知数的值愈接近方程的根．会估算一元二次方程的近似解是解题的关键．
根据图表数据找出一元二次方程等于0时，未知数的值的范围，即可得到答案．
【解答】
解：∵x=1.6时，x2−x−1.1=−0.14，x=1.7时，x2−x−1.1=0.09，
∴一元二次方程x2−x−1.1=0的解的范围是1.6故选：C．
8.【答案】D
【解析】解：根据作图可知：EF垂直平分BD，
∴BO=DO，
∵四边形ABCD是平行四边形，
∴AD=BC，AD//BC，
∴∠EDO=∠FBO，
∵∠BOF=∠DOE，
∴△BOF≌△DOE(ASA)，
∴BF=DE，OE=OF，故B，C正确；
无法证明DE=CD，故D错误；
故选：D．
根据作图可知：EF垂直平分BD，根据线段垂直平分线的性质得到BO=DO，根据平行四边形的性质得到AD=BC，AD//BC，根据全等三角形的性质得到BF=DE，OE=OF，故B，C正确；无法证明DE=CD，故D错误．
本题考查了作图−基本作图，垂直平分线的性质，尺规作图，菱形的判定与性质，全等三角形的判定与性质以及勾股定理等知识，掌握菱形的判定与性质是解答本题的关键．
9.【答案】D
【解析】解：∵O(0,0)，A(0,4)，
∴OA=4，
∵四边形AOCD为矩形，AO=4，
∴∠A=∠AOC=90°，
根据折叠的性质可得，∠AEF=∠OEF=90°，OE=AE=12AO=2，AO=ON=4，
∴EF//OC//AD，
如图，过点N作NB⊥OC于点B，

则四边形OBNE为矩形，
∴BN=OE=2，OB=EN，
在Rt△OBN中，OB= ON2−BN2= 42−22=2 3，
∴点N的坐标为(2 3,2)．
故选：D．
根据题意可得OA=4，由折叠可知∠AEF=∠OEF=90°，OE=AE=12AO=2，AO=ON=4，得到EF//OC//AD，过点N作NB⊥OC于点B，BN=OE=2，OB=EN，再根据勾股定理求得OB= ON2−BN2=2 3，以此即可得到点N的坐标．
本题主要考查坐标与图形、折叠的性质、矩形的性质、勾股定理，熟练掌握折叠的性质是解题关键．
10.【答案】D
【解析】解：根据题意，可得DP=t cm，BM=t cm，
∵AD=8cm，BC=6cm，
∴AP=(8−t)cm，CM=(6−t)cm，
当四边形ABMP为矩形时，AP=BM，
即8−t=t，
解得t=4，
故A选项不符合题意；
当四边形CDPM为平行四边形，DP=CM，
即t=6−t，
解得t=3，
故B选项不符合题意；
当CD=PM时，分两种情况：
①四边形CDPM是平行四边形，
此时CM=PD，
即6−t=t，
解得t=3，
②四边形CDPM是等腰梯形，
过点M作MG⊥AD于点G，过点C作CH⊥AD于点H，如图所示：

则∠MGP=∠CHD=90°，
∵PM=CD，GM=HC，
∴△MGP≌△CHD(HL)，
∴GP=HD，
∵AG=AP+GP=8−t+t−(6−t)2，
又∵BM=t，
∴8−t+t−(6−t)2=t，
解得t=5，
综上，当CD=PM时，t=3s或5s，
故C选项不符合题意，D选项符合题意，
故选：D．
根据题意，表示出DP，BM，AP和CM的长，当四边形ABMP为矩形时，根据AP=BM，列方程求解即可；当四边形CDPM为平行四边形，根据DP=CM，列方程求解即可；当CD=PM时，分两种情况：①四边形CDPM是平行四边形，②四边形CDPM是等腰梯形，分别列方程求解即可．
本题考查了矩形的判定，平行四边形的判定，全等三角形的判定和性质，涉及动点问题，用含t的代数式表示出各线段的长是解题的关键．
11.【答案】3：4
【解析】解：x：y=3：4，
故答案为：3：4．
根据等式的性质，可得答案．
本题考查了比例的性质，利用等式的性质是解题关键．
12.【答案】x≥3
【解析】解：∵代数式 x−3有意义，
∴x−3≥0，
解得：x≥3，
故答案为：x≥3．
根据 x−3有意义得出x−3≥0，再求出答案即可．
本题考查了二次根式有意义的条件，能根据 x−3有意义得出x−3≥0是解此题的关键．
13.【答案】1
【解析】解：∵最简根式 2与 5m−3是同类二次根式，
∴5m−3=2，
5m=5，
m=1，
故答案为：1．
根据同类二次根式的定义可得5m−3=2，然后进行计算即可解答．
本题考查了同类二次根式，最简二次根式，熟练掌握同类二次根式的定义是解题的关键．
14.【答案】0
【解析】解：∵a是方程x2+2x−2=0的实数根，
∴a2+2a−2=0，
∴a2=−2a+2，
∴a2+3a+b=−2a+2+3a+b=a+b+2，
∵a、b是方程x2+2x−2=0的两个实数根，
∴a+b=−2，
∴a2+3a+b=−2+2=0．
故答案为：0．
先根据一元二次方程根的定义得到a2=−2a+2，则a2+3a+b化为a+b+2，再利用根与系数的关系得a+b=−2，然后利用整体代入的方法计算．
本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0(a≠0)的两根时，x1+x2=−ba，x1x2=ca.也考查了一元二次方程的解．
15.【答案】(80 5−160)cm
【解析】解：弦AB=80cm，点C是靠近点B的黄金分割点，设BC=x，则AC=80−x，
∴80−x80= 5−12，解方程得，x=120−40 5，
点D是靠近点A的黄金分割点，设AD=y，则BD=80−y，
∴80−y80= 5−12，解方程得，y=120−40 5，
∴C，D之间的距离为80−x−y=80−120+40 5−120+40 5=80 5−160，
故答案为：(80 5−160)cm．
黄金分割点是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比．其比值是一个无理数，用分数表示为 5−12，由此即可求解．
本题主要考查线段成比例，掌握线段成比例，黄金分割点的定义是解题的关键．
16.【答案】 5
【解析】解：连接OP，
∵四边形ABCD是菱形，
∴AC⊥BD，AO=12AC=5，BO=12BD=52，
∴AB= 52+(52)2=5 52，
∵PE⊥OA于点E，PF⊥OB于点F，
∴∠EOF=∠OEP=∠OFP=90°，
∴四边形OEPF是矩形，
∴EF=OP，
∵当OP取最小值时，EF的值最小，
∴当OP⊥AB时，OP最小，
∴S△ABO=12OA⋅OB=12AB⋅OP，
∴OP=5×525 52= 5，
∴EF的最小值为 5，
故答案为： 5．
连接OP，根据菱形的性质得到AC⊥BD，AO=12AC=5，BD=12BD=52，根据勾股定理得到AB=5 52，根据矩形的性质得到EF=OP，根据三角形的面积公式即可得到结论．
本题考查了矩形的判定和性质，垂线段最短，菱形的性质，熟练掌握垂线段最短是解题的关键．
17.【答案】解：原式=2 2+2− 2−2
= 2．
【解析】直接利用二次根式的性质以及绝对值的性质、负整数指数幂的性质分别化简，进而得出答案．
此题主要考查了实数的运算，正确化简各数是解题关键．
18.【答案】解：移项得x2−4x=3，
配方得x2−4x+4=3+4，
即(x−2)2= 7，
开方得x−2=± 7，
∴x1=2+ 7，x2=2− 7．
【解析】本题考查配方法解一元二次方程．
根据配方法即可解．
19.【答案】证明：∵四边形ABCD是矩形，
∴AB=CD，AB//CD．
∴∠BAC=∠DCA．
∵AE=CF，
∴AE+EF=CF+EF，即AF=CE．
在△ABF和△CDE中，AB=CD∠BAF=∠DCEAF=CE，
∴△ABF≌△CDE(SAS)，
∴∠ABF=∠CDE．
【解析】证明△ABF≌△CDE(SAS)，即可得出∠ABF=∠CDE．
本题考查了矩形的性质、全等三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等是解题的关键．
20.【答案】解：(1)如图，△A1B1C1即为所作．

(2)如图，△A2B2C2即为所作．
【解析】(1)分别作出点A、B、C绕点O顺时针旋转90°后的对应点A1、B1、C1，顺次连接即可；
(2)分别连接AO、BO、CO并分别延长到点A2、B2、C2，使得OA2=2AO、OB2=2BO、OC2=2CO，顺次连接A2、B2、C2即可．
此题考查了旋转和位似图形的作图，熟练掌握作图方法是解题的关键．
21.【答案】(1)证明：∵AB=AC，
∴∠B=∠C，
又∵∠BDE=∠CAD，
∴△BDE∽△CAD；
(2)解：∵△BDE∽△CAD，
∴BECD=BDAC，
∴39=4AC，
∴AC=12，
∴AB=12．
【解析】(1)先利用等腰三角形的性质得出∠B=∠C，再由∠BDE=∠CAD可证得△BDE∽△CAD；
(2)由相似三角形的性质可得出答案．
本题考查了相似三角形的判定与性质，熟练掌握相似三角形的判定方法是解题的关键．
22.【答案】2x (40−x)
【解析】解：(1)设每件衣服降价x元，则每天销售量增加2x件，每件商品盈利(40−x)元．
故答案为：2x，(40−x)；
(2)设每件服装降价x元，则每件的销售利润为(40−x)元，平均每天的销售量为(20+2x)件，
依题意得：(120−x−80)(20+2x)=1200，
整理得：x2−30x+200=0，
解得：x1=10，x2=20．
又∵需要让利于顾客，
∴x=20．
答：每件服装降价20元时，能让利于顾客并且商家平均每天能盈利1200元．
(1)根据每件服装降价1元，那么平均每天可多售出2件，可得结论；
(2)设每件服装降价x元，则每件的销售利润为(120−x−80)元，平均每天的销售量为(20+2x)件，利用商家每天销售该款服装获得的利润=每件的销售利润×日销售量，即可得出关于x的一元二次方程，解之即可得出x的值，再结合需要让利于顾客，即可得出每件服装应降价20元．
本题考查了一元二次方程的应用以及根的判别式，解题的关键是：(1)找准等量关系，正确列出一元二次方程；(2)牢记“当Δ<0时，方程无实数根”．
23.【答案】(1)证明：∵∠BAD=∠CAE，
∴∠BAD+∠CAD=∠CAE+CAD，即∠BAC=∠DAE，
∵AB=AC，AD=AE，
∴∠B=∠ACB=12(180°−∠BAC)，∠ADE=∠E=12(180°−∠DAE)，
∵∠BAC=∠DAE，
∴∠B=∠ACB=∠ADE=∠E，
∴△ABC∽△ADE；
(2)证明：如图，

∵AE//BC，
∴∠AEF=∠CDF，∠EAF=∠DCF，
由(1)可知，∠DCF=∠ADF=∠AEF，
∴∠ADF=∠CDF，
∵DA=DC，
∴AF=CF，
在△AEF和△CDF中，
∠AEF=∠CDF∠EAF=∠DCFAF=CF，
∴△AEF≌△CDF(AAS)，
∴AE=CD，
∵AE//CD，AE=CD，
∴四边形ADCE为平行四边形，
∵DA=DC，
∴平行四边形ADCE为菱形．
【解析】(1)由等角加同角相等可得∠BAC=∠DAE，由△ABC和△ADE的顶角相等，且都是等腰三角形，以此即可证明△ABC∽△ADE；
(2)根据平行线的性质得∠AEF=∠CDF，∠EAF=∠DCF，进而得到∠ADF=∠CDF，由等腰三角形三线合一的性质可得AF=CF，再通过AAS证明△AEF≌△CDF，得到AE=CD，由对边平行且相等的四边形是平行四边形可证明四边形ADCE为平行四边形，最后根据一组邻边相等的平行四边形是菱形即可证明四边形ADCE是菱形．
本题主要考查相似三角形的判定、等腰三角形的性质、平行线的性质、全等三角形的判定与性质，熟练菱形的判定方法是解题关键．菱形的判定：①菱形定义：一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形).②四条边都相等的四边形是菱形．③对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”)．
24.【答案】解：(1)3 5− 2=3( 5+ 2)( 5− 2)( 5+ 2)= 5+ 2；
(2)因为a=1 2+1= 2−1( 2+1)( 2+1)= 2−1，
所以a+1= 2，
所以(a+1)2=2，
即a2+2a+1=2，
所以a2+2a=1，
所以2a2+4a−1=2(a2+2a)−1=2×1−1=1．
【解析】(1)把分子分母都乘以( 5+ 2)，然后利用平方差公式计算；
(2)先分母有理化得到a= 2−1，再移项平方得到a2+2a=1，接着把2a2+4a−1变形为2(a2+2a)−1，然后利用整体代入的方法计算．
本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．也考查了分母有理化．
25.【答案】2t (6−t)
【解析】解：(1)∵点P从A开始沿边AB向点B以1cm/s的速度移动，点Q从点B开始沿边BC向点C以2cm/s的速度移动，
∴BQ=2t cm，AP=t cm，
∴PB=(6−t)cm，
故答案为：2t，(6−t)；
(2)由题意得S△PBQ=12×BP×BQ=12×(6−t)×2t=5，
∴t2−6t+5=0，
解得：t1=1，t2=5(不合题意，舍去)，
∴当t=1时，△PBQ的面积等于5cm2；
(3)存在，理由如下：
若四边形APQC的面积等于△ABC面积的23，
∴△PBQ的面积等于△ABC面积的13，
∴12(6−t)×2t=13×12×6×8，
∴t2−6t+8=0，
解得：t=2或t=4，
当t=2时，BQ=4cm
当t=4时，BQ=8cm，四边形APQC变为三角形，不合题意，舍去，
∴存在时刻t，使四边形APQC的面积等于△ABC面积的23，t的值为2．
(1)由路程=速度×时间，可直接求解；
(2)由三角形的面积公式可求解；
(3)由题意可得△PBQ的面积等于△ABC面积的13，由三角形的面积公式可求解．
本题是四边形综合题，考查了三角形的面积公式，一元二次方程的应用，灵活运用这些性质解决问题是解题的关键．
26.【答案】(1)证明：∵△ABC和△BDE分别是等边三角形，
∴AB=CB，BE=BD，
∴∠ABC=∠DBE=60°，
∴∠ABC+∠CBE=∠DBE+∠CBE，
即∠ABE=∠CBD，
在△ABE和△CBD中，
AB=CB∠ABE=∠CBDBE=BD，
∴△ABE≌△CBD(SAS)，
∴AE=CD；
(2)解：AE= 2CD，
证明：∵△ABC，△DEB都是等腰直角三角形，
∴BA= 2BC，BE= 2BD，
∴ABBC=BEBD= 2，
∵∠ABC=∠DBE=45°，
∴∠ABE=∠CBD，
∴△ABE∽△CBD，
∴AECD=ABBC= 2，
∴AE= 2CD；
(3)解：①如图，连接AE，

由(2)知△ADG∽△ACE，
∴DGCE=ADAC= 22，
∴DG= 22CE，
∵四边形ABCD是正方形，
∴AD=BC=6 2，
∴AC= 2BC=12，
∵四边形AFEG是正方形，
∴∠AGE=90°，GE=AG=4，
∵C，G，E三点共线．
∴CG= AC2−AG2=8 2，
∴CE=CG−EG=8 2−4，
∴DG= 22CE=8−2 2；
②如图，连接AE，

由(2)知△ADG∽△ACE，
∴DGCE=ADAC= 22，
∴DG= 22CE，
∵四边形ABCD是正方形，
∴AD=BC=6 2，
∴AC= 2BC=12，
∵四边形AFEG是正方形，
∴∠AGE=90°，GE=AG=4，
∵C，G，E三点共线．
∴CG= AC2−AG2=8 2，
∴CE=CG+EG=8 2+4，
∴DG= 22CE=8+2 2；
综上，当C，G，E三点共线时，DG的长度为8−2 2或8+2 2．
【解析】(1)证明△ABE≌△CBD(SAS)，由全等三角形的性质得出AE=CD；
(2)证明△ABE∽△CBD，由相似三角形的性质得出ABBC=BEBD= 2，则可得出结论；
(3)分两种情况画出图形，证明△ADG∽△ACE，根据相似三角形的判定和性质以及勾股定理即可得出答案．
本题属于四边形综合题，考查了旋转的性质，等腰直角三角形的性质，等边三角形的性质，正方形的性质，相似三角形的判定和性质，全等三角形的判定与性质等知识，解题的关键是正确寻找相似三角形解决问题，学会添加常用辅助线，构造全等三角形解决问题．
x
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
x2−x−1.1
−0.99
−0.86
−0.71
−0.54
−0.35
−0.14
0.09
0.34
0.61