山东省烟台市2021-2023三年中考数学真题分类汇编-02填空题知识点分类

这是一份山东省烟台市2021-2023三年中考数学真题分类汇编-02填空题知识点分类，共18页。试卷主要包含了，使得运算结果等于24等内容，欢迎下载使用。

山东省烟台市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一．有理数的混合运算（共2小题）
1．（2022•烟台）如图，是一个“数值转换机”的示意图．若x＝﹣5，y＝3，则输出结果为 　 　．

2．（2022•烟台）小明和同学们玩扑克牌游戏．游戏规则是：从一副扑克牌（去掉“大王”“小王”）中任意抽取四张，根据牌面上的数字进行混合运算（每张牌上的数字只能用一次），使得运算结果等于24．小明抽到的牌如图所示，请帮小明列出一个结果等于24的算式 　 　．

二．科学记数法—表示较大的数（共1小题）
3．（2023•烟台）“北斗系统”是我国自主建设运行的全球卫星导航系统，国内多个导航地图采用北斗优先定位．目前，北斗定位服务日均使用量已超过3600亿次．3600亿用科学记数法表示为 　 　．
三．计算器—基础知识（共1小题）
4．（2023•烟台）如图，利用课本上的计算器进行计算，其按键顺序及结果如下：
①按键的结果为4；
②按键的结果为8；
③按键的结果为0.5；
④按键的结果为25．
以上说法正确的序号是 　 　．

四．因式分解-运用公式法（共1小题）
5．（2022•烟台）把x2﹣4因式分解为 　 　．
五．二次根式有意义的条件（共1小题）
6．（2021•烟台）若代数式在实数范围内有意义，则x的取值范围为 　 　．
六．一元一次方程的应用（共1小题）
7．（2021•烟台）幻方历史悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1～9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则a的值为 　 　．

七．坐标确定位置（共1小题）
8．（2022•烟台）观察如图所示的象棋棋盘，若“兵”所在的位置用（1，3）表示，“炮”所在的位置用（6，4）表示，那么“帅”所在的位置可表示为 　 　．

八．动点问题的函数图象（共2小题）
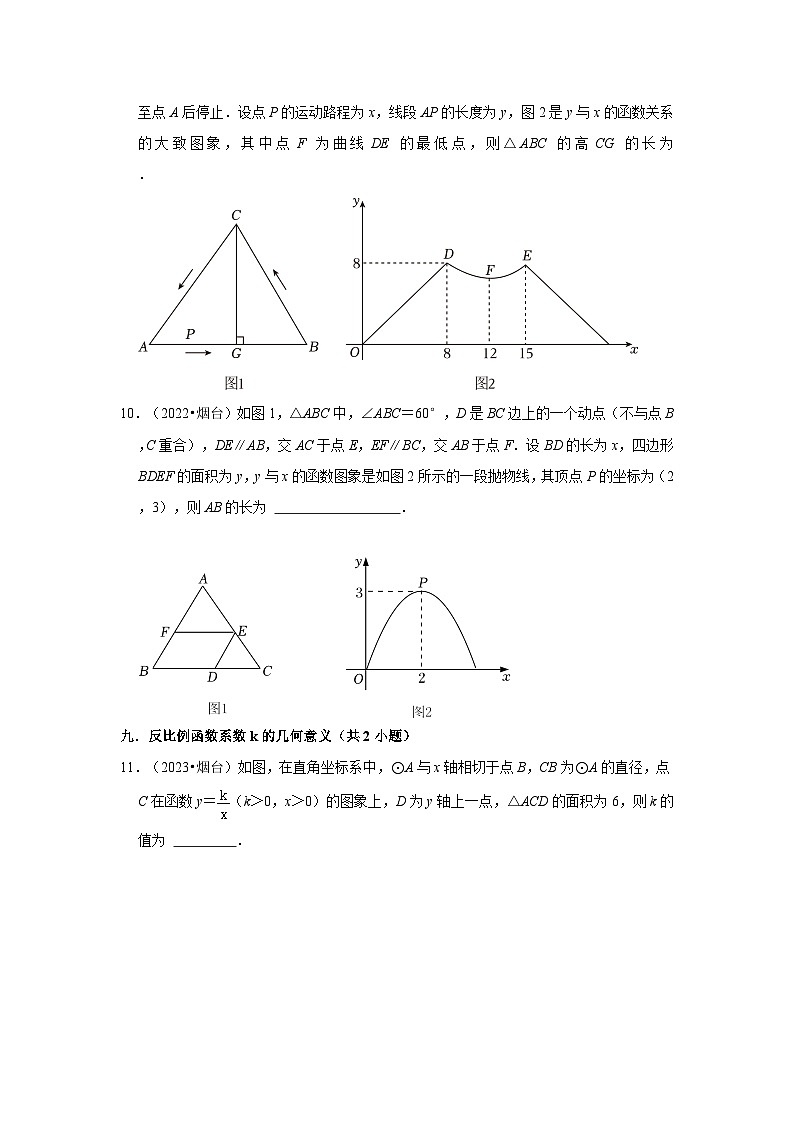
9．（2023•烟台）如图1，在△ABC中，动点P从点A出发沿折线AB→BC→CA匀速运动至点A后停止．设点P的运动路程为x，线段AP的长度为y，图2是y与x的函数关系的大致图象，其中点F为曲线DE的最低点，则△ABC的高CG的长为 　 　．

10．（2022•烟台）如图1，△ABC中，∠ABC＝60°，D是BC边上的一个动点（不与点B，C重合），DE∥AB，交AC于点E，EF∥BC，交AB于点F．设BD的长为x，四边形BDEF的面积为y，y与x的函数图象是如图2所示的一段抛物线，其顶点P的坐标为（2，3），则AB的长为 　 　．


九．反比例函数系数k的几何意义（共2小题）
11．（2023•烟台）如图，在直角坐标系中，⊙A与x轴相切于点B，CB为⊙A的直径，点C在函数y＝（k＞0，x＞0）的图象上，D为y轴上一点，△ACD的面积为6，则k的值为 　 　．

12．（2022•烟台）如图，A，B是双曲线y＝（x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为 　 　．

一十．平行线的性质（共1小题）
13．（2023•烟台）一杆古秤在称物时的状态如图所示，已知∠1＝102°，则∠2的度数为 　 　．

一十一．圆周角定理（共1小题）
14．（2023•烟台）如图，将一个量角器与一把无刻度直尺水平摆放，直尺的长边与量角器的外弧分别交于点A，B，C，D，连接AB，则∠BAD的度数为 　 　．

一十二．三角形的外接圆与外心（共1小题）
15．（2021•烟台）如图，在正方形网格中，每个小正方形的边长都是1，⊙O是△ABC的外接圆，点A，B，O在网格线的交点上，则sin∠ACB的值是 　 　．

一十三．图形的剪拼（共1小题）
16．（2021•烟台）综合实践活动课上，小亮将一张面积为24cm2，其中一边BC为8cm的锐角三角形纸片（如图1），经过两刀裁剪，拼成了一个无缝隙、无重叠的矩形BCDE（如图2），则矩形的周长为 　 　cm．

一十四．相似三角形的判定与性质（共1小题）
17．（2021•烟台）《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆AB，从木杆的顶端B观察井水水岸D，视线BD与井口的直径AC交于点E，如果测得AB＝1米，AC＝1.6米，AE＝0.4米，那么CD为 　 　米．

一十五．解直角三角形的应用-仰角俯角问题（共1小题）
18．（2021•烟台）数学兴趣小组利用无人机测量学校旗杆高度，已知无人机的飞行高度为40米，当无人机与旗杆的水平距离是45米时，观测旗杆顶部的俯角为30°，则旗杆的高度约为 　 　米．
（结果精确到1米，参考数据：≈1.41，≈1.73）


山东省烟台市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一．有理数的混合运算（共2小题）
1．（2022•烟台）如图，是一个“数值转换机”的示意图．若x＝﹣5，y＝3，则输出结果为 　13　．

【答案】见试题解答内容
【解答】解：当x＝﹣5，y＝3时，
（x2+y0）
＝×[（﹣5）2+30]
＝×（25+1）
＝×26
＝13，
故答案为：13．
2．（2022•烟台）小明和同学们玩扑克牌游戏．游戏规则是：从一副扑克牌（去掉“大王”“小王”）中任意抽取四张，根据牌面上的数字进行混合运算（每张牌上的数字只能用一次），使得运算结果等于24．小明抽到的牌如图所示，请帮小明列出一个结果等于24的算式 　5×6﹣2×3（答案不唯一）　．

【答案】5×6﹣2×3（答案不唯一）．
【解答】解：由题意得：
5×6﹣2×3
＝30﹣6
＝24，
故答案为：5×6﹣2×3（答案不唯一）．
二．科学记数法—表示较大的数（共1小题）
3．（2023•烟台）“北斗系统”是我国自主建设运行的全球卫星导航系统，国内多个导航地图采用北斗优先定位．目前，北斗定位服务日均使用量已超过3600亿次．3600亿用科学记数法表示为 　3.6×1011　．
【答案】3.6×1011．
【解答】解：将3600亿用科学记数法表示为3.6×1011．
故答案为：3.6×1011．
三．计算器—基础知识（共1小题）
4．（2023•烟台）如图，利用课本上的计算器进行计算，其按键顺序及结果如下：
①按键的结果为4；
②按键的结果为8；
③按键的结果为0.5；
④按键的结果为25．
以上说法正确的序号是 　①③　．

【答案】①③．
【解答】解：①按键的结果为＝4；故①正确，符合题意；
②按键的结果为4+（﹣2）3＝﹣4；故②不正确，不符合题意；
③按键的结果为sin（45°﹣15° ）＝sin30°＝0.5；故③正确，符合题意；④按键的结果为（3﹣）×22＝10；故④不正确，不符合题意；
综上：正确的有①③．
故答案为：①③．
四．因式分解-运用公式法（共1小题）
5．（2022•烟台）把x2﹣4因式分解为 　（x+2）（x﹣2）　．
【答案】（x+2）（x﹣2）．
【解答】解：x2﹣4＝（x+2）（x﹣2），
故答案为：（x+2）（x﹣2）．
五．二次根式有意义的条件（共1小题）
6．（2021•烟台）若代数式在实数范围内有意义，则x的取值范围为 　x≤2　．
【答案】见试题解答内容
【解答】解：依题意，得
2﹣x≥0，
解得，x≤2．
故答案是：x≤2．
六．一元一次方程的应用（共1小题）
7．（2021•烟台）幻方历史悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1～9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则a的值为 　2　．

【答案】2．
【解答】解：幻方右下角的数字为15﹣8﹣3＝4，
幻方第二行中间的数字为15﹣6﹣4＝5．
依题意得：8+5+a＝15，
解得：a＝2．
故答案为：2．
七．坐标确定位置（共1小题）
8．（2022•烟台）观察如图所示的象棋棋盘，若“兵”所在的位置用（1，3）表示，“炮”所在的位置用（6，4）表示，那么“帅”所在的位置可表示为 　（4，1）　．

【答案】见试题解答内容
【解答】解：如图所示：

“帅”所在的位置：（4，1），
故答案为：（4，1）．
八．动点问题的函数图象（共2小题）
9．（2023•烟台）如图1，在△ABC中，动点P从点A出发沿折线AB→BC→CA匀速运动至点A后停止．设点P的运动路程为x，线段AP的长度为y，图2是y与x的函数关系的大致图象，其中点F为曲线DE的最低点，则△ABC的高CG的长为 　　．

【答案】．
【解答】解：如图过点A作AQ⊥BC于点Q，当点P与Q重合时，在图2中F点表示当AB+BQ＝12时，点P到达点Q，此时当P在BC上运动时，AP最小，

∴BC＝7，BQ＝4，QC＝3，
在Rt△ABQ中，AB＝8，BQ＝4，
∴AQ＝，
∵S△ABC＝AB×CG＝AQ×BC，
∴CG＝．
故答案为：．
10．（2022•烟台）如图1，△ABC中，∠ABC＝60°，D是BC边上的一个动点（不与点B，C重合），DE∥AB，交AC于点E，EF∥BC，交AB于点F．设BD的长为x，四边形BDEF的面积为y，y与x的函数图象是如图2所示的一段抛物线，其顶点P的坐标为（2，3），则AB的长为 　2　．


【答案】见试题解答内容
【解答】解：∵抛物线的顶点为（2，3），过点（0，0），
∴x＝4时，y＝0，
∴BC＝4，
作FH⊥BC于H，当BD＝2时，▱BDEF的面积为3，

∵3＝2FH，
∴FH＝，
∵∠ABC＝60°，
∴BF＝＝，
∵DE∥AB，
∴AB＝2BF＝2，
故答案为：2．
九．反比例函数系数k的几何意义（共2小题）
11．（2023•烟台）如图，在直角坐标系中，⊙A与x轴相切于点B，CB为⊙A的直径，点C在函数y＝（k＞0，x＞0）的图象上，D为y轴上一点，△ACD的面积为6，则k的值为 　24　．

【答案】24．
【解答】解：过点A作AE⊥y轴于点E，

设⊙A的半径为r，
∵⊙A与x轴相切于点B，
∴AC＝AB＝r，BC＝2r，
设AE＝a，
则点C的坐标为（a，2r），
∴k＝2ar，
∵，
∴，
即：ar＝12，
∴k＝2ar＝24．
故答案为：24．
12．（2022•烟台）如图，A，B是双曲线y＝（x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为 　6　．

【答案】6．
【解答】解：因为D为AC的中点，△AOD的面积为3，
所以△AOC的面积为6，
所以k＝12＝2m．
解得：m＝6．
故答案为：6．
一十．平行线的性质（共1小题）
13．（2023•烟台）一杆古秤在称物时的状态如图所示，已知∠1＝102°，则∠2的度数为 　78°　．

【答案】78°．
【解答】解：如图，
由题意得：AB∥CD，
∴∠2＝∠BCD，
∵∠1＝102°，
∴∠BCD＝78°，
∴∠2＝78°，
故答案为：78°．

一十一．圆周角定理（共1小题）
14．（2023•烟台）如图，将一个量角器与一把无刻度直尺水平摆放，直尺的长边与量角器的外弧分别交于点A，B，C，D，连接AB，则∠BAD的度数为 　52.5°　．

【答案】52.5°．
【解答】解：设量角器的圆心是O，连接OD，OB，
∵∠BOD＝130°﹣25°＝105°，
∴∠BAD＝∠BOD＝52.5°．
故答案为：52.5°．

一十二．三角形的外接圆与外心（共1小题）
15．（2021•烟台）如图，在正方形网格中，每个小正方形的边长都是1，⊙O是△ABC的外接圆，点A，B，O在网格线的交点上，则sin∠ACB的值是 　　．

【答案】．
【解答】解：如图，连接AO并延长交⊙O于D，
由圆周角定理得：∠ACB＝∠ADB，
由勾股定理得：AD＝＝2，
∴sin∠ACB＝sin∠ADB＝＝＝，
故答案为：．

一十三．图形的剪拼（共1小题）
16．（2021•烟台）综合实践活动课上，小亮将一张面积为24cm2，其中一边BC为8cm的锐角三角形纸片（如图1），经过两刀裁剪，拼成了一个无缝隙、无重叠的矩形BCDE（如图2），则矩形的周长为 　22　cm．

【答案】22．
【解答】解：延长AT交BC于点P，

∵AP⊥BC，
∴•BC•AP＝24，
∴×8×AP＝24，
∴AP＝6（cm），
由题意，AT＝PT＝3（cm），
∴BE＝CD＝PT＝3（cm），
∵DE＝BC＝8cm，
∴矩形BCDE的周长为8+8+3+3＝22（cm）．
故答案为：22．
一十四．相似三角形的判定与性质（共1小题）
17．（2021•烟台）《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆AB，从木杆的顶端B观察井水水岸D，视线BD与井口的直径AC交于点E，如果测得AB＝1米，AC＝1.6米，AE＝0.4米，那么CD为 　3　米．

【答案】3．
【解答】解：由题意知：AB∥CD，
则∠BAE＝∠C，∠B＝∠CDE，
∴△ABE∽△CDE，
∴，
∴，
∴CD＝3米，
故答案为：3．
一十五．解直角三角形的应用-仰角俯角问题（共1小题）
18．（2021•烟台）数学兴趣小组利用无人机测量学校旗杆高度，已知无人机的飞行高度为40米，当无人机与旗杆的水平距离是45米时，观测旗杆顶部的俯角为30°，则旗杆的高度约为 　14　米．
（结果精确到1米，参考数据：≈1.41，≈1.73）

【答案】14．
【解答】解：过O点作OC⊥AB于C点，

∵当无人机与旗杆的水平距离是45米时，观测旗杆顶部的俯角为30°，
∴AC＝45米，∠CAO＝30°，
∴OC＝AC•tan30°＝（米），
∴旗杆的高度＝40﹣15≈14（米），
故答案为：14．