浙江省金华市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类

这是一份浙江省金华市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类，共35页。试卷主要包含了0+﹣2sin30°+|﹣5|，＞x+1，的函数关系，，点B在直线l，，直线BC与直线PD相交于点E，问题，已知等内容，欢迎下载使用。
浙江省金华市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
一．实数的运算（共1小题）
1．（2023•金华）计算：（﹣2023）0+﹣2sin30°+|﹣5|．
二．解一元一次不等式（共1小题）
2．（2022•金华）解不等式：2（3x﹣2）＞x+1．
三．一次函数的应用（共1小题）
3．（2023•金华）兄妹俩放学后沿图1中的马路从学校出发，到书吧看书后回家，哥哥步行先出发，途中速度保持不变：妹妹骑车，到书吧前的速度为200米/分，图2中的图象分别表示两人离学校的路程s（米）与哥哥离开学校的时间t（分）的函数关系．
（1）求哥哥步行的速度．
（2）已知妹妹比哥哥迟2分钟到书吧．
①求图中a的值；
②妹妹在书吧待了10分钟后回家，速度是哥哥的1.6倍，能否在哥哥到家前追上哥哥？若能，求追上时兄妹俩离家还有多远；若不能，说明理由．

四．一次函数综合题（共1小题）
4．（2021•金华）在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．
（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．
①若BA＝BO，求证：CD＝CO．
②若∠CBO＝45°，求四边形ABOC的面积．
（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB的长；若不存在，请说明理由．

五．反比例函数综合题（共1小题）
5．（2021•金华）背景：点A在反比例函数y＝（k＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形．如图1，点A在第一象限内，当AC＝4时，小李测得CD＝3．
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系．请帮助小李解决下列问题．
（1）求k的值．
（2）设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”．如图2，小李画出了x＞0时“Z函数”的图象．
①求这个“Z函数”的表达式．
②补画x＜0时“Z函数”的图象，并写出这个函数的性质（两条即可）．
③过点（3，2）作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标．

六．二次函数的应用（共1小题）
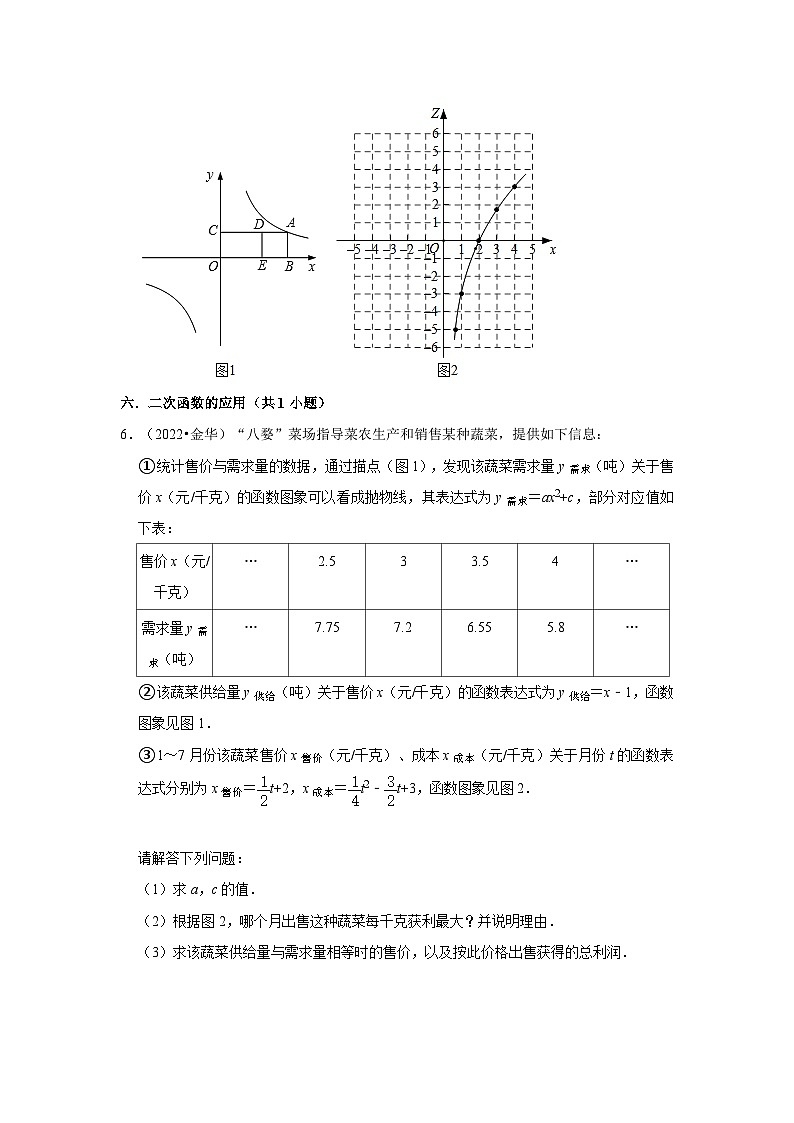
6．（2022•金华）“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：
①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量y需求（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为y需求＝ax2+c，部分对应值如下表：
售价x（元/千克）
…
2.5
3
3.5
4
…
需求量y需求（吨）
…
7.75
7.2
6.55
5.8
…
②该蔬菜供给量y供给（吨）关于售价x（元/千克）的函数表达式为y供给＝x﹣1，函数图象见图1．
③1～7月份该蔬菜售价x售价（元/千克）、成本x成本（元/千克）关于月份t的函数表达式分别为x售价＝t+2，x成本＝t2﹣t+3，函数图象见图2．

请解答下列问题：
（1）求a，c的值．
（2）根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．
（3）求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．

七．二次函数综合题（共1小题）
7．（2023•金华）如图，直线y＝与x轴，y轴分别交于点A，B，抛物线的顶点P在直线AB上，与x轴的交点为C，D，其中点C的坐标为（2，0），直线BC与直线PD相交于点E．
（1）如图2，若抛物线经过原点O．
①求该抛物线的函数表达式；
②求的值．
（2）连结PC，∠CPE与∠BAO能否相等？若能，求符合条件的点P的横坐标；若不能，试说明理由．

八．勾股定理的逆定理（共1小题）
8．（2023•金华）如图，为制作角度尺，将长为10，宽为4的矩形OABC分割成4×10的小正方形网格，在该矩形边上取点P，来表示∠POA的度数，阅读以下作图过程，并回答下列问题：

作法（如图）
结论
①在CB上取点P1，使CP1＝4．
∠P1OA＝45°，点P1表示45°．
②以O为圆心，8为半径作弧，与BC交于点P2．
∠P2OA＝30°，点P2表示30°．
③分别以O，P2为圆心，大于OP2长度一半的长为半径作弧，相交于点E，F，连接EF与BC相交于点P3．
…
④以P2为圆心，OP2的长为半径作弧，与射线CB交于点D，连结OD交AB于点P4．
…
（1）分别求点P3，P4表示的度数．
（2）用直尺和圆规在该矩形的边上作点P5，使该点表示37.5°（保留作图痕迹，不写作法）．

九．三角形综合题（共1小题）
9．（2023•金华）问题：如何设计“倍力桥”的结构？
图1是搭成的“倍力桥”，纵梁a，c夹住横梁b，使得横梁不能移动，结构稳固．
图2是长为l（cm），宽为3cm的横梁侧面示意图，三个凹槽都是半径为1cm的半圆，圆心分别为O1，O2，O3，O1M＝O1N，O2Q＝O3P＝2cm，纵梁是底面半径为1cm的圆柱体，用相同规格的横梁、纵梁搭“桥”，间隙忽略不计．
探究1：图3是“桥”侧面示意图，A，B为横梁与地面的交点，C，E为圆心，D，H1，H2是横梁侧面两边的交点，测得AB＝32cm，点C到AB的距离为12cm，试判断四边形CDEH1的形状，并求l的值．
探究2：若搭成的“桥”刚好能绕成环，其侧面示意图的内部形成一个多边形．
①若有12根横梁绕成环，图4是其侧面示意图，内部形成十二边形H1H2H3…H12，求l的值；
②若有n根横梁绕成的环（n为偶数，且n≥6），试用关于n的代数式表示内部形成的多边形H1H2H3…Hn的周长．

一十．矩形的性质（共1小题）
10．（2021•金华）已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠BOC＝120°，AB＝2．
（1）求矩形对角线的长；
（2）过O作OE⊥AD于点E，连结BE．记∠ABE＝α，求tanα的值．

一十一．四边形综合题（共1小题）
11．（2022•金华）如图，在菱形ABCD中，AB＝10，sinB＝，点E从点B出发沿折线B﹣C﹣D向终点D运动．过点E作点E所在的边（BC或CD）的垂线，交菱形其它的边于点F，在EF的右侧作矩形EFGH．
（1）如图1，点G在AC上．求证：FA＝FG．
（2）若EF＝FG，当EF过AC中点时，求AG的长．
（3）已知FG＝8，设点E的运动路程为s．当s满足什么条件时，以G，C，H为顶点的三角形与△BEF相似（包括全等）？


一十二．正多边形和圆（共1小题）
12．（2022•金华）如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：
作法 如图2．
1．作直径AF．
2．以F为圆心，FO为半径作圆弧，与⊙O交于点M，N．
3．连接AM，MN，NA．
（1）求∠ABC的度数．
（2）△AMN是正三角形吗？请说明理由．
（3）从点A开始，以DN长为边长，在⊙O上依次截取点，再依次连接这些分点，得到正n边形，求n的值．

一十三．圆的综合题（共1小题）
13．（2021•金华）在扇形AOB中，半径OA＝6，点P在OA上，连结PB，将△OBP沿PB折叠得到△O′BP．
（1）如图1，若∠O＝75°，且BO′与所在的圆相切于点B．
①求∠APO′的度数．
②求AP的长．
（2）如图2，BO′与相交于点D，若点D为的中点，且PD∥OB，求的长．


浙江省金华市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
参考答案与试题解析
一．实数的运算（共1小题）
1．（2023•金华）计算：（﹣2023）0+﹣2sin30°+|﹣5|．
【答案】7．
【解答】解：（﹣2023）0+﹣2sin30°+|﹣5|
＝1+2﹣2×+5
＝1+2﹣1+5
＝7．
二．解一元一次不等式（共1小题）
2．（2022•金华）解不等式：2（3x﹣2）＞x+1．
【答案】x＞1．
【解答】解：去括号得：
6x﹣4＞x+1，
移项得：
6x﹣x＞4+1，
合并同类项得：
5x＞5，
∴x＞1．
三．一次函数的应用（共1小题）
3．（2023•金华）兄妹俩放学后沿图1中的马路从学校出发，到书吧看书后回家，哥哥步行先出发，途中速度保持不变：妹妹骑车，到书吧前的速度为200米/分，图2中的图象分别表示两人离学校的路程s（米）与哥哥离开学校的时间t（分）的函数关系．
（1）求哥哥步行的速度．
（2）已知妹妹比哥哥迟2分钟到书吧．
①求图中a的值；
②妹妹在书吧待了10分钟后回家，速度是哥哥的1.6倍，能否在哥哥到家前追上哥哥？若能，求追上时兄妹俩离家还有多远；若不能，说明理由．

【答案】（1）100m/min．
（2）①a＝6．
②能，追上时兄妹俩离家300米远．
【解答】解：（1）由A（8，800）可知哥哥的速度为：800÷8＝100（m/min）．
（2）①∵妹妹骑车到书吧前的速度为200米/分，
∴妹妹所用时间t为：800÷200＝4（min）．
∵妹妹比哥哥迟2分钟到书吧，
∴a＝8+2﹣4＝6．
②由（1）可知：哥哥的速度为100m/min，
∴设BC所在直线为s1＝100t+b，
将B（17，800）代入得：800＝100×17+b，
解得b＝﹣900．
∴BC所在直线为：s1＝100t﹣900．
当s1＝1900时，t哥哥＝28．
∵返回时妹妹的速度是哥哥的1.6倍，
∴妹妹的速度是160米/分．
∴设妹妹返回时得解析式为s2＝160t+b，
将F（20，800）代入得800＝160×20+b，
解得b＝﹣2400，
∴s2＝160t﹣2400．
令s1＝s2，则有100t﹣900＝160t﹣2400，
解得t＝25＜28，
∴妹妹能追上哥哥，
此时哥哥所走得路程为：800+（25﹣17）×100＝1600（米）．
兄妹俩离家还有1900﹣1600＝300（米），
即妹妹能追上哥哥，追上时兄妹俩离家300米远．
四．一次函数综合题（共1小题）
4．（2021•金华）在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．
（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．
①若BA＝BO，求证：CD＝CO．
②若∠CBO＝45°，求四边形ABOC的面积．
（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB的长；若不存在，请说明理由．

【答案】（1）①证明见解答过程；②；
（2）存在，OB 的长度为：4或4+或4﹣或9或1；
【解答】（1）①证明：∵BC⊥AB，CO⊥BO，
∴∠ABC＝∠BOC＝90°，
∴∠BAD+∠ADB＝∠COD+∠DOB＝90°，
∵BA＝BO，
∴∠BAD＝∠DOB，
∴∠ADB＝∠COD，
∵∠ADB＝∠CDO，
∴∠COD＝∠CDO，
∴CD＝CO；
②解：过A作AM⊥OB于M，过M作MN⊥y轴于N，如图：

∵M在直线l：y＝x上，设M（m，m），
∴MN＝|m|＝﹣m，ON＝|m|＝﹣m，
Rt△MON中，tan∠OMN＝＝，
而OA∥MN，
∴∠AOM＝∠OMN，
∴tan∠AOM＝，即＝，
设AM＝3n，则OM＝8n，
Rt△AOM中，AM2+OM2＝OA2，
又A的坐标为（﹣，0），
∴OA＝，
∴（3n）2+（8n）2＝（）2，
解得n＝1（n＝﹣1舍去），
∴AM＝3，OM＝8，
∵∠CBO＝45°，CO⊥BO，
∴△BOC是等腰直角三角形，
∵BC⊥AB，∠CBO＝45°，
∴∠ABM＝45°，
∵AM⊥OB，
∴△ABM是等腰直角三角形，
∴AM＝BM＝3，BO＝CO＝OM﹣BM＝5，
∴等腰直角三角形△ABM中，AB＝AM＝3，
等腰直角三角形△BOC中，BC＝BO＝5，
∴S△ABC＝AB•BC＝15，S△BOC＝BO•CO＝，
∴S四边形ABOC＝S△ABC+S△BOC＝；
（2）解：存在点B，使得以A，B，C为顶点的三角形与△BCO相似，理由如下：
（一）过A作AM⊥OB于M，当B在线段OM或OM延长线上时，如图：


由（1）②可知：AM＝3，OM＝8，
设OB＝x，则BM＝|8﹣x|，AB＝，
∵CO⊥BO，AM⊥BO，AB⊥BC，
∴∠AMB＝∠BOC＝90°，∠ABM＝90°﹣∠OBC＝∠BCO，
∴△AMB∽△BOC，
∴＝，即＝，
∴OC＝，
Rt△BOC中，BC＝＝，
∵∠ABC＝∠BOC＝90°，
∴以A，B，C为顶点的三角形与△BCO相似，分两种情况：
①若＝，则＝，
解得x＝4，
∴此时OB＝4；
②若＝，则＝，
解得x1＝4+，x2＝4﹣，x3＝9，x4＝﹣1（舍去），
∴OB＝4+或OB＝4﹣或OB＝9；
（二）当B在线段MO延长线上时，如图：

由（1）②可知：AM＝3，OM＝8，
设OB＝x，则BM＝8+x，AB＝，
∵CO⊥BO，AM⊥BO，AB⊥BC，
∴∠AMB＝∠BOC＝90°，∠ABM＝90°﹣∠OBC＝∠BCO，
∴△AMB∽△BOC，
∴＝，即＝，
∴OC＝•（8+x），
Rt△BOC中，BC＝＝•，
∵∠ABC＝∠BOC＝90°，
∴以A，B，C为顶点的三角形与△BCO相似，需满足＝，即＝，
解得x1＝﹣9（舍去），x2＝1，
∴OB＝1，
综上所述，以A，B，C为顶点的三角形与△BCO相似，则OB 的长度为：4或4+或4﹣或9或1；
五．反比例函数综合题（共1小题）
5．（2021•金华）背景：点A在反比例函数y＝（k＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形．如图1，点A在第一象限内，当AC＝4时，小李测得CD＝3．
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系．请帮助小李解决下列问题．
（1）求k的值．
（2）设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”．如图2，小李画出了x＞0时“Z函数”的图象．
①求这个“Z函数”的表达式．
②补画x＜0时“Z函数”的图象，并写出这个函数的性质（两条即可）．
③过点（3，2）作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标．

【答案】见试题解答内容
【解答】解：（1）∵AC＝4，CD＝3，
∴AD＝AC﹣CD＝1，
∵四边形ABED是正方形，
∴AB＝1，
∵AC⊥y轴，AB⊥x轴，
∴∠ACO＝∠COB＝∠OBA＝90°，
∴四边形ABOC是矩形，
∴OB＝AC＝4，
∴A（4，1），
∴k＝4．

（2）①由题意，A（x，x﹣z），
∴x（x﹣z）＝4，
∴z＝x﹣．

②图象如图所示．

性质1：x＞0时，y随x的增大而增大．
性质2：图象是中心对称图形．

③设直线的解析式为z＝kx+b，
把（3，2）代入得到，2＝3k+b，
∴b＝2﹣3k，
∴直线的解析式为z＝kx+2﹣3k，
由，消去z得到，（k﹣1）x2+（2﹣3k）x+4＝0，
当k≠1时，当Δ＝0时，（2﹣3k）2﹣4（k﹣1）×4＝0，
解得k＝或2，
当k＝时，方程为x2﹣x+4＝0，解得x1＝x2＝6．
当k＝2时，方程为x2﹣4x+4＝0，解得x1＝x2＝2．
当k＝1时．方程的解为x＝4，符合题意，
另外直线x＝3，也符合题意，此时交点的横坐标为3，
综上所述，满足条件的交点的横坐标为2或3或4或6．
六．二次函数的应用（共1小题）
6．（2022•金华）“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：
①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量y需求（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为y需求＝ax2+c，部分对应值如下表：
售价x（元/千克）
…
2.5
3
3.5
4
…
需求量y需求（吨）
…
7.75
7.2
6.55
5.8
…
②该蔬菜供给量y供给（吨）关于售价x（元/千克）的函数表达式为y供给＝x﹣1，函数图象见图1．
③1～7月份该蔬菜售价x售价（元/千克）、成本x成本（元/千克）关于月份t的函数表达式分别为x售价＝t+2，x成本＝t2﹣t+3，函数图象见图2．

请解答下列问题：
（1）求a，c的值．
（2）根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．
（3）求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．

【答案】（1）a的值为﹣，c的值为9；（2）在4月份出售这种蔬菜每千克获利最大；（3）该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元．
【解答】解：（1）把（3，7.2），（4，5.8）代入y需求＝ax2+c，
，
②﹣①，得7a＝﹣1.4，
解得：a＝﹣，
把a＝﹣代入①，得c＝9，
∴a的值为﹣，c的值为9；
（2）设这种蔬菜每千克获利w元，根据题意，
w＝x售价﹣x成本＝t+2﹣（t2﹣t+3）＝﹣（t﹣4）2+3，
∵﹣＜0，且1≤t≤7，
∴当t＝4时，w有最大值，
答：在4月份出售这种蔬菜每千克获利最大；
（3）当y供给＝y需求时，x﹣1＝﹣x2+9，
解得：x1＝5，x2＝﹣10（舍去），
∴此时售价为5元/千克，
则y供给＝x﹣1＝5﹣1＝4（吨）＝4000（千克），
令t+2＝5，解得t＝6，
∴w＝﹣（t﹣4）2+3＝﹣×（6﹣4）2+3＝2，
∴总利润为w•y＝2×4000＝8000（元），
答：该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元．
七．二次函数综合题（共1小题）
7．（2023•金华）如图，直线y＝与x轴，y轴分别交于点A，B，抛物线的顶点P在直线AB上，与x轴的交点为C，D，其中点C的坐标为（2，0），直线BC与直线PD相交于点E．
（1）如图2，若抛物线经过原点O．
①求该抛物线的函数表达式；
②求的值．
（2）连结PC，∠CPE与∠BAO能否相等？若能，求符合条件的点P的横坐标；若不能，试说明理由．

【答案】（1）①y＝﹣x2+3x；②的值为．
（2）∠CPE与∠BAO能相等，点P的横坐标为．
【解答】解：（1）①∵抛物线经过原点O（0，0）、C（2，0），
∴对称轴为直线x＝1，
当x＝1时，y＝×1+＝，
∴抛物线的顶点P（1，），
设抛物线的解析式为y＝a（x﹣1）2+，把C（2，0）代入，得a+＝0，
解得：a＝﹣，
∴y＝﹣（x﹣1）2+＝﹣x2+3x，
∴该抛物线的函数表达式为y＝﹣x2+3x；
②∵直线y＝与x轴，y轴分别交于点A，B，
∴A（﹣2，0），B（0，），
设直线OP的解析式为y＝kx，把P（1，）代入，得：k＝，
∴直线OP的解析式为y＝x，
如图，过点B作BF∥x轴交OP于点F，则点F的纵坐标与点B的纵坐标相同，

∴＝x，
解得：x＝，
∴F（，），
∴BF＝，
∵BF∥OC，
∴△BEF∽△CEO，
∴＝＝＝，
∴的值为．
（2）如图，过点P作PF⊥x轴于点F，
设P（m，m+），则F（m，0），
∴PF＝m+，AF＝m﹣（﹣2）＝m+2，AC＝2﹣（﹣2）＝4，

在Rt△APF中，AP2＝AF2+PF2＝（m+2）2+（m+）2＝m2+9m+9，
若∠CPE＝∠BAO，
∵∠PCD＝∠ACP，
∴△CPD∽△CAP，
∴∠CDP＝∠CPA，
∵PC＝PD，
∴∠CDP＝∠ACP，
∴∠PCD＝∠CPA，
∴AP＝AC，
∴m2+9m+9＝16，
解得：m1＝﹣（舍去），m2＝，
∴∠CPE与∠BAO能相等，点P的横坐标为．
八．勾股定理的逆定理（共1小题）
8．（2023•金华）如图，为制作角度尺，将长为10，宽为4的矩形OABC分割成4×10的小正方形网格，在该矩形边上取点P，来表示∠POA的度数，阅读以下作图过程，并回答下列问题：

作法（如图）
结论
①在CB上取点P1，使CP1＝4．
∠P1OA＝45°，点P1表示45°．
②以O为圆心，8为半径作弧，与BC交于点P2．
∠P2OA＝30°，点P2表示30°．
③分别以O，P2为圆心，大于OP2长度一半的长为半径作弧，相交于点E，F，连接EF与BC相交于点P3．
…
④以P2为圆心，OP2的长为半径作弧，与射线CB交于点D，连结OD交AB于点P4．
…
（1）分别求点P3，P4表示的度数．
（2）用直尺和圆规在该矩形的边上作点P5，使该点表示37.5°（保留作图痕迹，不写作法）．

【答案】（1）点P3表示 60°，点P4表示 15°；
（2）见解析．
【解答】解：①∵四边形OABC是矩形，
∴BC∥OA，
∴∠OP2C＝∠P2OA＝30°，
由作图可知，EF是 OP2 的中垂线，
∴OP3＝P3P2；
∴∠P3OP2＝∠P3P2O＝30°，
∴∠P3OA＝∠P3OP2+∠P2OA＝60°，
∴点 P3 表示 60°；
②作图可知，P2D＝P2O，
∴∠P2OD＝∠P2DO，
∵CB∥OA，
∴∠P2DO＝∠DOA；
∴，
∴点P4表示 15°；
答：点P3表示60°，点P4表示15°；
（2）作∠P3OP4 的角平分线交BC于P5，点P5即为所求作的点，如图：

∵点P3表示 60°，点P4表示 15°，
∴∠P3OP4＝60°﹣15°＝45°，
∴∠P3OP4+∠P4OA＝22.5°+15°＝37.5°，
∴P5 表示 37.5°．
九．三角形综合题（共1小题）
9．（2023•金华）问题：如何设计“倍力桥”的结构？
图1是搭成的“倍力桥”，纵梁a，c夹住横梁b，使得横梁不能移动，结构稳固．
图2是长为l（cm），宽为3cm的横梁侧面示意图，三个凹槽都是半径为1cm的半圆，圆心分别为O1，O2，O3，O1M＝O1N，O2Q＝O3P＝2cm，纵梁是底面半径为1cm的圆柱体，用相同规格的横梁、纵梁搭“桥”，间隙忽略不计．
探究1：图3是“桥”侧面示意图，A，B为横梁与地面的交点，C，E为圆心，D，H1，H2是横梁侧面两边的交点，测得AB＝32cm，点C到AB的距离为12cm，试判断四边形CDEH1的形状，并求l的值．
探究2：若搭成的“桥”刚好能绕成环，其侧面示意图的内部形成一个多边形．
①若有12根横梁绕成环，图4是其侧面示意图，内部形成十二边形H1H2H3…H12，求l的值；
②若有n根横梁绕成的环（n为偶数，且n≥6），试用关于n的代数式表示内部形成的多边形H1H2H3…Hn的周长．

【答案】（1）CDEH1为菱形，l＝22cm；
（2）①l＝（16+6）cm，②（）cm．
【解答】解：探究1：①四边形CDEH1是菱形，理由如下：
由图1可知，CD∥EH1，ED∥CH1，
∴CDEH1为平行四边形，
∵桥梁的规格是相同的，
∴桥梁的宽度相同，即四边形CDEH1每条边上的高相等，
∵平行四边形CDEH1的面积等于边长乘这条边上的高，
∴CDEH1每条边相等，
∴CDEH1为菱形．
②如图1，过点C作CM⊥AB于点M．

由题意，得CA＝CB，CM＝12cm，AB＝32cm，
∴AM＝AB＝16cm，
在Rt△CAM中，CA2＝AM2+CM2，
∴CA＝20（cm），
∴l＝CA+2＝22（cm），
故答案为：l＝22cm．
探究2：①如图2，过点C作CN⊥H1H2于点N，

由题意，得∠H1CH2＝120°，CH1＝CH2，CN＝3cm，
∴∠CH1N＝30°，
∴CH1＝2CN＝6cm，H1N＝cm，
又∵四边形CDEH1是菱形，
∴EH1＝CH1＝6cm，
∴l＝2（2+6+3）＝（16+6）cm，
故答案为：l＝（16+6）cm．
②如图3，过点C作CN⊥H1H2于点N．

由题意，形成的多边形为正n边形，
∴外角∠CH1H2＝，
在Rt△CNH1中，H1N＝（cm），
又∵CH1＝CH2，CN⊥H1H2，
∴H1H2＝2H1N＝cm，
∴形成的多边形的周长为（）cm．
故答案为：（）cm．
一十．矩形的性质（共1小题）
10．（2021•金华）已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠BOC＝120°，AB＝2．
（1）求矩形对角线的长；
（2）过O作OE⊥AD于点E，连结BE．记∠ABE＝α，求tanα的值．

【答案】（1）矩形对角线的长为4；
（2）tanα＝．
【解答】解：（1）∵∠BOC＝120°，
∴∠AOB＝60°，
∵四边形ABCD是矩形，
∴∠BAD＝90°，AC＝BD，AO＝OC，BO＝DO，
∴AO＝BO，
∴△AOB是等边三角形，
∴AB＝AO＝BO，
∵AB＝2，
∴BO＝2，
∴BD＝2BO＝4，
∴矩形对角线的长为4；
（2）由勾股定理得：AD＝＝＝2，
∵OA＝OD，OE⊥AD于点E，
∴AE＝DE＝AD＝，
∴tanα＝＝．
一十一．四边形综合题（共1小题）
11．（2022•金华）如图，在菱形ABCD中，AB＝10，sinB＝，点E从点B出发沿折线B﹣C﹣D向终点D运动．过点E作点E所在的边（BC或CD）的垂线，交菱形其它的边于点F，在EF的右侧作矩形EFGH．
（1）如图1，点G在AC上．求证：FA＝FG．
（2）若EF＝FG，当EF过AC中点时，求AG的长．
（3）已知FG＝8，设点E的运动路程为s．当s满足什么条件时，以G，C，H为顶点的三角形与△BEF相似（包括全等）？


【答案】（1）证明见解析部分；
（2）AG的长为5或7；
（3）s的值为1或或或10≤s≤12．
【解答】解：（1）如图1中，

∵四边形ABCD是菱形，
∴BA＝BC，
∴∠BAC＝∠BCA，
∵FG∥BC．
∴∠AGF＝∠ACB，
∴∠AGF＝∠FAG，
∴FA＝FG；

（2）设AC的中点为O．
①如图2中，当点E在BC上时，过点A作AM⊥CB于点M．

在Rt△ABM中，AM＝AB•sinB＝10×＝6，
∴BM＝＝＝8，
∴FG＝EF＝AM＝6，CM＝BC﹣BM＝2，
∵OA＝OC，OE∥AM，
∴CE＝EM＝CM＝1，
∴AF＝EM＝1，
∴AG＝AF+FG＝7．
②如图3中，当点E在CD上时，过点A作AN⊥CD于N．

同法FG＝EF＝AN＝6，CN＝2，AF＝EN＝CN，
∴AG＝FG﹣AF＝6﹣1＝5，
综上所述，满足条件的AG的长为5或7；

（3）过点A作AM⊥BC于点M，AN⊥CD于点N．
①当点E在线段BM上时，0＜s≤8，设EF＝3x，则BE＝4x，GH＝EF＝3x．
a、若点H点C的左侧，s+8＜10，即0＜s＜2，如图4，

CH＝BC﹣BH＝10﹣（4x+8）＝2﹣4x，
由△GHC∽△FEB，可得＝，即＝，
∴＝，解得x＝，
经检验x＝是分式方程的解，
∴s＝4x＝1．
由△GHC∽△BEF，可得＝，即＝，
∴＝，解得x＝，
∴s＝4x＝．
b、若点H在点C的右侧，s+8＞10，即2＜s≤8，如图5，

CH＝BH﹣BC＝（4x+8）﹣10＝4x﹣2，
由△GHC∽△FEB，可得＝，即＝，
∴＝，方程无解，
由△GHC∽△BEF，可得＝，即＝，
∴＝，解得x＝，
∴s＝4x＝．
②当点E在线段MC上时，8＜s≤10，如图6，

EF＝6，EH＝8，BE＝s，
∴BH＝BE+EH＝s+8，CH＝BH﹣BC＝s﹣2，
由△GHC∽△FEB，可得＝，即＝，
∴＝，方程无解，
由△GHC∽△FEB，可得＝，即＝，
∴＝，解得s＝1±（舍弃）
③当点E在线段CN上时，10＜s≤12，如图7，过点C作CJ⊥AB于点J，

在Rt△BJC中，BC＝10，CJ＝6，BJ＝8，
∵EH＝BJ＝8，JF＝CE，
∴BJ+JF＝EH+CE，即CH＝BF，
∴△GHC≌△EFB，符合题意，此时10＜s≤12．
④当点E在线段DN上时，12＜s＜20，
∵∠EFB＞90°，
∴△GHC与△BEF不相似．
综上所述．满足条件的s的值为1或或或10≤s≤12．

一十二．正多边形和圆（共1小题）
12．（2022•金华）如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：
作法 如图2．
1．作直径AF．
2．以F为圆心，FO为半径作圆弧，与⊙O交于点M，N．
3．连接AM，MN，NA．
（1）求∠ABC的度数．
（2）△AMN是正三角形吗？请说明理由．
（3）从点A开始，以DN长为边长，在⊙O上依次截取点，再依次连接这些分点，得到正n边形，求n的值．

【答案】（1）108°；
（2）△AMN是正三角形，理由见解答；
（3）15．
【解答】解：（1）∵五边形ABCDE是正五边形，
∴∠ABC＝＝108°，
即∠ABC＝108°；
（2）△AMN是正三角形，
理由：连接ON，NF，如图，
由题意可得：FN＝ON＝OF，
∴△FON是等边三角形，
∴∠NFA＝60°，
∴∠NMA＝60°，
同理可得：∠ANM＝60°，
∴∠MAN＝60°，
∴△MAN是正三角形；
（3）连接OD，如图，
∵∠AMN＝60°，
∴∠AON＝120°，
∵∠AOD＝＝144°，
∴∠NOD＝∠AOD﹣∠AON＝144°﹣120°＝24°，
∵360°÷24°＝15，
∴n的值是15．

一十三．圆的综合题（共1小题）
13．（2021•金华）在扇形AOB中，半径OA＝6，点P在OA上，连结PB，将△OBP沿PB折叠得到△O′BP．
（1）如图1，若∠O＝75°，且BO′与所在的圆相切于点B．
①求∠APO′的度数．
②求AP的长．
（2）如图2，BO′与相交于点D，若点D为的中点，且PD∥OB，求的长．

【答案】（1）①60°．
②6﹣2．
（2）．
【解答】解：（1）①如图1中，∵BO′是⊙O的切线，
∴∠OBO′＝90°，
由翻折的性质可知，∠OBP＝∠PBO′＝45°，∠OPB＝∠BPO′，
∵∠AOB＝75°，
∴∠OPB＝∠BPO′＝180°﹣75°﹣45°＝60°，
∴∠OPO′＝120°，
∴∠APO′＝180°﹣∠OPO′＝180°﹣120°＝60°．

②如图1中，过点B作BH⊥OA于H，在BH上取一点F，使得OF＝FB，连接OF．
∵∠BHO＝90°，
∴∠OBH＝90°﹣∠BOH＝15°，
∵FO＝FB，
∴∠FOB＝∠FBO＝15°，
∴∠OFH＝∠FOB+∠FBO＝30°，
设OH＝m，则HF＝m，OF＝FB＝2m，
∵OB2＝OH2+BH2，
∴62＝m2+（m+2m）2，
∴m＝或﹣（舍弃），
∴OH＝，BH＝，
在Rt△PBH中，PH＝＝，
∴PA＝OA﹣OH﹣PH＝6﹣﹣＝6﹣2．
解法二：连接OO′交PB于T，则BP⊥′OO′，
在Rt△OBT中，OT＝OB×sin45°＝3．
在Rt△OTP中，OP＝＝2，
∴AP＝OA﹣OP＝6﹣2．

（2）如图2中，连接AD，OD．
∵＝，
∴AD＝BD，∠AOD＝∠BOD，
由翻折的性质可知，∠OBP＝∠PBD，
∵PD∥OB，
∴∠DPB＝∠OBP，
∴∠DPB＝∠PBD，
∴DP＝DB＝AD，
∴∠DAP＝∠APD＝∠AOB，
∵AO＝OD＝OB，AD＝DB，
∴△AOD≌△BOD，
∴∠OBD＝∠OAD＝∠AOB＝2∠BOD，
∵OB＝OD，
∴∠OBD＝∠ODB＝2∠DOB，
∴∠DOB＝36°，
∴∠AOB＝72°，
∴的长＝＝．