小学数学5 三角形三角形的特性教案及反思

这是一份小学数学5 三角形三角形的特性教案及反思，共10页。教案主要包含了基于经验，理解三角形的三边关系，基于实践操作，交流判定方法，拓展反思，总结提升等内容，欢迎下载使用。
 人教版数学四年级下册《三角形的三边关系》教学设计 教学目标1.知道三角形任意两边的和大于第三边，理解和掌握“较短两边的和大于第三边”的判断方法。2.在操作活动中探究三角形的三边关系，在探索和发现的过程中培育推理意识。3.体验数据分析、数形结合等思想方法在探究过程中的作用。教学重难点教学重点:探索并发现三角形任意两边的和大于第三边。教学难点:较短两根小棒的长度之和等于第三根小棒的长度时能不能围成三角形。教学过程一、基于经验，理解三角形的三边关系（一）借助生活经验，找到最近的路师：（出示图1）这是老师课前让大家做的一道题，能看懂他的想法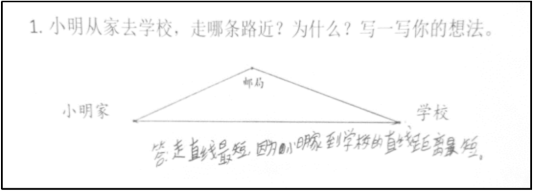？图1生：上面那条路要转个弯，下面这条路是走直线，肯定是下面这条路最短。生：两点之间线段最短。师：大家都同意这种想法吗？生：（齐）同意。师：在生活中遇到这种情况，我们肯定会走下面这条路，这是常识。在数学上，两点间的所有连线中线段最短，这条线段的长度叫做两点间的距离。（二）基于测量数据，验证最近的路师：（出示图2）这位同学量出了每条线段的长度，你能根据他的数据，说出小明家到学校的纸上距离是多少吗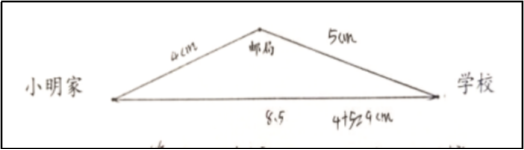？图2生：小明家到学校的纸上距离是8.5厘米。生：如果从邮局绕道的话，纸上距离就是4＋5＝9（厘米）。【思考：通过对前测的分析发现，学生有“走直线最短”的生活经验，教学应把学生朴素的生活理解改造成更加规范的数学表达——两点之间线段最短。之后呈现测量的方法，是为了让学生直观感受“两点之间线段最短”，强化“两点间的距离”这一概念，为后续推导三角形的三边关系打好基础。】（三）基于交流研讨，得出初步结论师：这三条路组成的图形是一个什么图形？（学生回答：三角形）设三角形三条边的边长分别设为a、b、c（标注字母，呈现图3）根据刚才的结论，我们可以用一个什么算式来表示这三条边之间的关系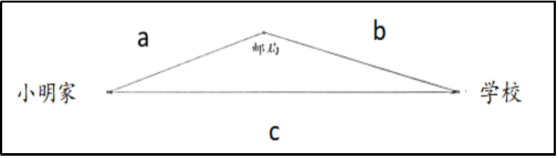？图3生：a＋b＞c。师：按照上面的思路，你还能得出三角形三条边的其他关系吗？生：如果小明从家去邮局，直接走过去最近，我们可以得到b＋c＞a。生：如果小明从学校去邮局，直接走过去最近，我们可以得到a＋c＞b。师：根据a＋b＞c、b＋c＞a、a＋c＞b这三个式子，你能用一句来概括三角形的三边关系吗？生：三角形两条边的和大于剩下的边。生：我觉得应该是三角形任意两边的和大于剩下的边。师：你能解释一下“任意”两个字的意思吗？生：就是随便哪两条边的长度加起来，都肯定大于第三边。因为从图上可以看出，走两条路肯定比走一条路要远。（四）基于丰富案例，再次验证结论师：（板书：三角形任意两边的和大于第三边）刚才我们的研究都基于同一个三角形，那么是不是所有的三角形都符合这个结论呢？请你画一个三角形，同桌交换验证。（学生动手操作实践、集体交流。）师：这样看来，至少我们画出来的这些三角形都符合这个结论。有没有人画出来的不符合这个结论？【思考：学生基于生活经验得出了“三角形任意两边的和大于剩下的边”这一结论，但还需在充分交流、研讨的基础上，通过大量的举例进行辨析和验证。虽然小学阶段对这一结论的验证过程属于不完全归纳，无法得出准确的推导过程，但经历这样的探究，可以发展学生的推理意识，帮助他们体会数学的严谨和理性。】二、基于实践操作，交流判定方法[出示：学具袋中有7根小棒（包含3厘米小棒3根，4厘米、5厘米、7厘米、8厘米小棒各1根），请你选择其中的3根小棒围一个三角形。想想哪些组合一定能围成三角形，哪些组合一定不能，为什么？先用小棒围一围，再用画草图的方式记录。]（一）交流能围成三角形的方案师：哪些情况能围成三角形？生：我选择了4厘米、7厘米、8厘米这3根小棒，能围成三角形。师：你能用跟刚才的结论解释吗？生：因为4＋7＞8，4＋8＞7，7＋8＞4，满足任意两边的和大于第三边，所以能围成三角形。生：我选择了3厘米、7厘米、8厘米这3根小棒，也可以围成三角形。我认为只要较短的两根小棒的长度和大于第三根小棒就可以确定了，因为另外两种组合，两根小棒中的一根已经比第三根长了，不用比就知道两根小棒的长度和肯定大于第三根。师：他说只要看较短两根的和是不是大于第三根就可以了，大家同意吗？生：（齐）同意。师：看来，我们的判断方法可以简化一下了。（板书：三角形较短的两边的和大于第三边）原来要看三组关系，现在只需看一组就行了。用这个方法来快速判断一下还有哪些情况是肯定能围成三角形的？生：“3、3、3”“3、3、4”“3、3、5”“3、4、5”“3、5、7”“4、5、7”“4、5、8”“5、7、8”一共8种。师：在这些三角形中，哪些比较特殊？生：我发现“3、3、3”是等边三角形，“3、3、4”“3、3、5”是等腰三角形。生：我发现“3、4、5”这个三角形比较特殊，应该是一个直角三角形。生：我知道，就是“勾三股四弦五”。师：对，你知道得真多！“3、4、5”是直角三角形，它是不是也满足较短的两边的和大于第三边？生：（齐）是。【思考：在利用性质判定“三根小棒能否围成三角形”的实践过程中，学生既要动用已经习得的三边关系结论，又要借助自行绘制的草图进行推理验证。在思考想象和动手实践的共同作用下，学生巩固了三角形的三边关系结论，进一步提炼出简洁的判定方法，并在实际应用过程中进行检验。讨论过程中，学生出现了“勾三股四弦五”的直角三角形判定方法，一方面，教师应肯定学生的课外学习成果，另一方面，也应发挥教学智慧，及时将课堂拉回原先的讨论中。】（二）交流不能围成三角形的方案师：有围不起来的吗？生：我选择了3厘米、4厘米、8厘米这3根小棒，发现围不成三角形。师：不对啊，4＋8＞3，两边之和大于第三边了，应该能围成三角形啊。生：虽然4＋8＞3符合“两边之和大于第三边”，但是3＋4＜8却不符合，所以不行。师：谁能再把他的话补充完整？生：我觉得要么看较短两边的和是否大于第三边，要么就把三组关系都比较完，才能得出结论，像老师这样只看其中一组是不行的。师：说得真好。还有其他围不成的情况吗？生：我选择了3厘米、4厘米、7厘米这3根小棒，发现也围不成。生：我选择的也是3厘米、4厘米、7厘米这3根小棒，我觉得能围成。师：请你们上来用小棒围一围。（学生演示，形成图4。）大家有什么想说的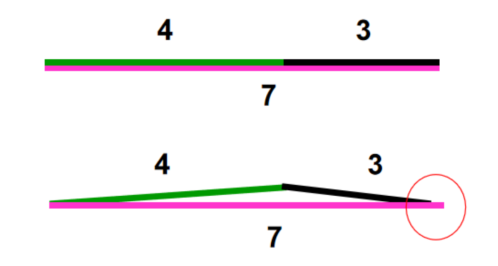？生：上面的那种围法正确，3＋4＝7，不可能围成三角形，短的两条边的和等于第三边，所以重合了。生：那下面围成的不是三角形吗？生：不是的，你看右边那里两条边没有首尾连接起来。如果3、4、7能围成三角形，那不就意味着走弯路和走直路一样长了吗？生：嗯，你说的有道理。师：（课件动态演示拼组过程）所以较短两边的和小于或者等于第三边，都不能围成三角形。像这样不能围成三角形的情况有哪些呢？生：一共有“3、3、7”“3、3、8”“3、4、7”“3、4、8”“3、5、8”这几种。师：最后这组“3、5、8”为什么不能围成三角形？生：因为3＋5＝8，较短两边的和等于第三边了。师：那么把哪根小棒的长度换一下，就可以围成三角形了？生：可以把8厘米这根换成比它短的就可以了。师：如果规定是整数的话，你觉得可以是哪些数？生：可以是7、6、5、4、3、2、1。生：我觉得2和1都不可以，因为“3、1、5”和“3、2、5”这两种情况都围不成三角形，较短两根小棒的和比第三根短了。师：那你觉得第三根小棒的长度应该是怎样的呢？生：应该比3＋5的和小，但是比5－3的差大，所以7、6、5、4、3都可以。师：如果边长可以是小数呢？生：那只要比2大、比8小就可以了。【思考：如果给学生提供小棒来探究围成三角形的情况，那么学生可以根据图像快速而直观地得出结论，对发展推理思维不利。因此，笔者给出了数据和“画草图”的提示，让学生先推理，在推理遇到困难时（如“3、4、7”这类临界状况），再借助图像和小棒直观判断，推理得出较短两边的和等于第三边时也不能围成三角形，充分锻炼学生的推理能力，发展他们的推理思维。后续通过对第三根小棒取值范围的讨论，帮助学生进一步巩固和理解三角形三边关系的同时，培育他们的推理意识。】三、拓展反思，总结提升师：把一根10厘米的小棒剪成三段，围成三角形，小明的第一刀剪在5厘米处，小红的第一刀剪在6厘米处，你觉得谁剪出的小棒能围成三角形？为什么？请大家开动脑筋试一试吧！没有思路的话，可以画草图分析。（学生画图探究，教师巡视引导。）生：小明的剪法不行。如果第一刀剪在5厘米处，那就变成了两根一样长的小棒，不管把哪一根小棒再剪成两段，这两段的和都等于第三根。小红的剪法可以。师：那么小红的第一刀剪完后，你觉得第二刀应该剪在哪里？你是怎么想的？生：第二刀应该剪在比较长的那一段上，不管剪在哪里，这两根小棒的长度都大于第三根（4厘米）。第二刀如果剪在4厘米的那一段，那么剪出来的两根小棒的和就一定小于第三根了，也就不能围成三角形了。生：不对！第二刀剪在长的那段上的时候，不能剪出小于1厘米或者等于1厘米的，不然和4厘米那段的和就小于第三段了。师：真棒！今天这节课我们有什么收获？生：我们知道了三角形任意两边的和大于第三边。生：我们明白了只要较短两条线段的和大于第三条线段，就肯定能围成三角形。【思考：基于对三角形三边关系的认识，学生借助画草图的方法判断第一刀和第二刀的下刀位置。对第一刀的判断比较简单，学生大多没有画草图分析，而对第二刀切在哪里的判断，学生如果没有画图，往往就会有所疏漏。“剪一刀”的活动充分调动了学生的空间想象力，引导他们在画图、操作的过程中逐步厘清三角形的三边关系，助推推理意识的发展。】