

江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)02选择题基础题①(含解析)
展开
这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)02选择题基础题①(含解析),共20页。
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题①
【考点目录】
一.绝对值(共1小题) 1
二.实数的性质(共1小题) 1
三.估算无理数的大小(共1小题) 1
四.同底数幂的除法(共1小题) 1
五.一元二次方程的应用(共1小题) 2
六.一次函数与一元一次不等式(共1小题) 2
九.专题:正方体相对两个面上的文字(共1小题) 3
一十.平行线的性质(共2小题) 3
一十一.三角形三边关系(共2小题) 3
一十二.等腰三角形的判定与性质(共1小题) 4
一十三.三角形中位线定理(共1小题) 4
一十四.矩形的性质(共1小题) 4
一十五.圆内接四边形的性质(共1小题) 4
一十六.切线的性质(共1小题) 5
一十七.相似三角形的判定与性质(共1小题) 5
一十八.相似三角形的应用(共1小题) 5
一十九.折线统计图(共1小题) 6
二十.加权平均数(共1小题) 6
二十一.众数(共1小题) 7
【专题练习】
一.绝对值(共1小题)
1.(2022•南京)已知实数a,b,a>b,下列结论中一定正确的是( )
A.|a|>|b| B.> C.a2>b2 D.a3>b3
二.实数的性质(共1小题)
2.(2022•无锡)5的相反数是( )
A.5 B.﹣5 C. D.﹣
三.估算无理数的大小(共1小题)
3.(2022•南京)估计12的算术平方根介于 ( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
四.同底数幂的除法(共1小题)
4.(2022•徐州)下列计算正确的是( )
A.a2•a6=a8 B.a8÷a4=a2
C.2a2+3a2=6a4 D.(﹣3a)2=﹣9a2
五.一元二次方程的应用(共1小题)
5.(2022•南通)李师傅家的超市今年1月盈利3000元,3月盈利3630元.若从1月到3月,每月盈利的平均增长率都相同,则这个平均增长率是( )
A.10.5% B.10% C.20% D.21%
六.一次函数与一元一次不等式(共1小题)
6.(2022•南通)根据图象,可得关于x的不等式kx>﹣x+3的解集是( )
A.x<2 B.x>2 C.x<1 D.x>1
七.反比例函数图象上点的坐标特征(共1小题)
7.(2022•无锡)已知一次函数y=x+2的图象上存在两个点,这两个点关于y轴的对称点恰好在反比例函数y=(k>0)的图象上,则k的范围是( )
A.0<k< B.0<k<1 C.0<k<2 D.0<k<4
八.几何体的展开图(共1小题)
8.(2022•常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
九.专题:正方体相对两个面上的文字(共1小题)
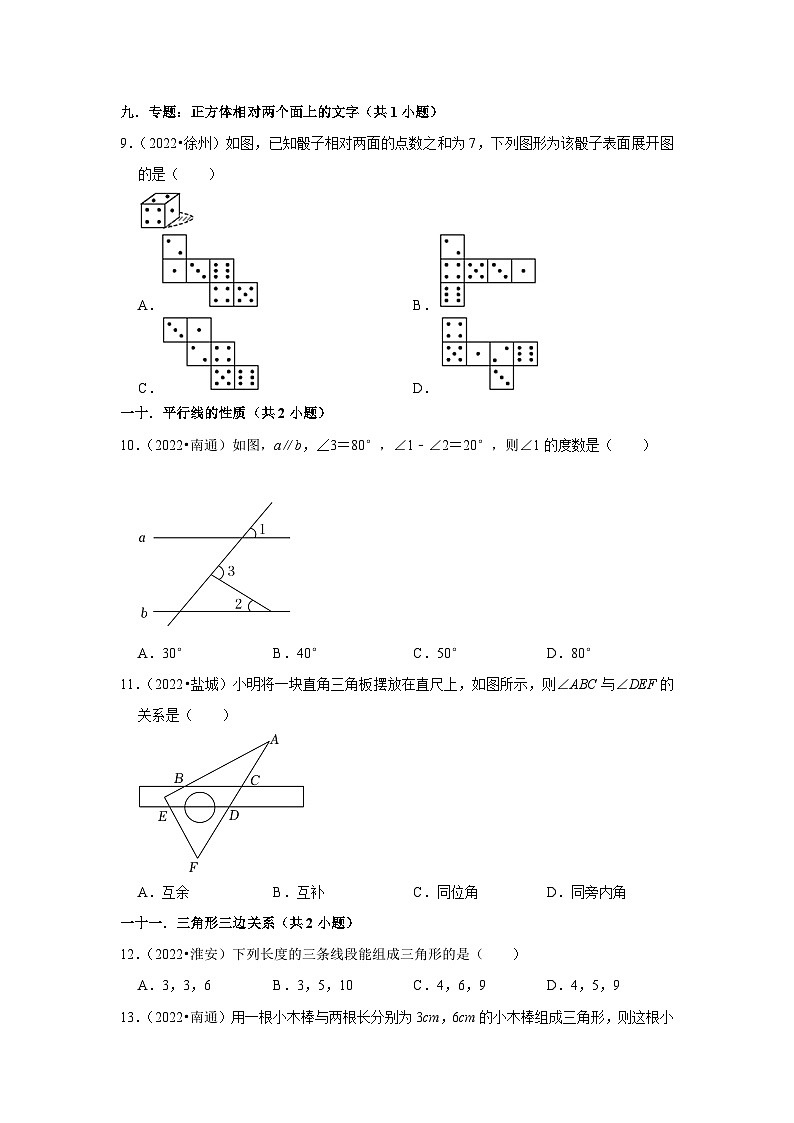
9.(2022•徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
一十.平行线的性质(共2小题)
10.(2022•南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是( )
A.30° B.40° C.50° D.80°
11.(2022•盐城)小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
一十一.三角形三边关系(共2小题)
12.(2022•淮安)下列长度的三条线段能组成三角形的是( )
A.3,3,6 B.3,5,10 C.4,6,9 D.4,5,9
13.(2022•南通)用一根小木棒与两根长分别为3cm,6cm的小木棒组成三角形,则这根小木棒的长度可以为( )
A.1cm B.2cm C.3cm D.4cm
一十二.等腰三角形的判定与性质(共1小题)
14.(2022•镇江)如图,点A、B、C、D在网格中小正方形的顶点处,AD与BC相交于点O,小正方形的边长为1,则AO的长等于( )
A.2 B. C. D.
一十三.三角形中位线定理(共1小题)
15.(2022•常州)如图,在△ABC中,D、E分别是AB、AC的中点.若DE=2,则BC的长是( )
A.3 B.4 C.5 D.6
一十四.矩形的性质(共1小题)
16.(2022•无锡)菱形具有而矩形不一定具有的性质是( )
A.对边平行 B.对角线互相平分
C.对角线互相垂直 D.对角互补
一十五.圆内接四边形的性质(共1小题)
17.(2022•淮安)如图,四边形ABCD是⊙O的内接四边形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.100° C.140° D.160°
一十六.切线的性质(共1小题)
18.(2022•无锡)如图,AB是⊙O的直径,AB=6,BC是⊙O的切线,D是AC的中点,OD=2,则AC的值为( )
A.10 B.8 C. D.
一十七.相似三角形的判定与性质(共1小题)
19.(2022•徐州)如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A.5 B.6 C. D.
一十八.相似三角形的应用(共1小题)
20.(2022•盐城)“跳眼法”是指用手指和眼睛估测距离的方法,
步骤:
第一步:水平举起右臂,大拇指紧直向上,大臂与身体垂直;
第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;
第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离的长度;
第四步:将横向距离乘以10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测点的距离值.
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图,该汽车的长度大约为4米,则汽车到观测点的距离约为( )
A.40米 B.60米 C.80米 D.100米
一十九.折线统计图(共1小题)
21.(2022•徐州)我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率﹣人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
二十.加权平均数(共1小题)
22.(2022•无锡)某食堂销售三种午餐盒饭的有关数据如表所示,该食堂销售午餐盒饭的平均价格是( )
品种
A
B
C
单价(元/份)
12
10
8
销售比例
15%
60%
25%
A.10.2元 B.10元 C.9.8元 D.9.5元
二十一.众数(共1小题)
23.(2022•淮安)某公司对25名营销人员4月份销售某种商品的情况统计如下:
销售量(件)
60
50
40
35
30
20
人数
1
4
4
6
7
3
则这25名营销人员销售量的众数是( )
A.50 B.40 C.35 D.30
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题①
参考答案与试题解析
一.绝对值(共1小题)
1.(2022•南京)已知实数a,b,a>b,下列结论中一定正确的是( )
A.|a|>|b| B.> C.a2>b2 D.a3>b3
【答案】D
【解答】解:A.由a>b,如1>﹣2,但|1|<|﹣2|,那么|a|>|b|不正确,故A不符合题意.
B.由a>b,如2>1,但,那么不正确,故B不符合题意.
C.由a>b,如1>﹣2,但12<(﹣2)2,那么a2>b2不正确,故C不符合题意.
D.由a>b,则a3>b3,那么C正确,故D符合题意.
故选:D.
二.实数的性质(共1小题)
2.(2022•无锡)5的相反数是( )
A.5 B.﹣5 C. D.﹣
【答案】B
【解答】解:实数5的相反数为﹣5.
故选:B.
三.估算无理数的大小(共1小题)
3.(2022•南京)估计12的算术平方根介于 ( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【答案】C
【解答】解:∵,
∴3<<4,
故选:C.
四.同底数幂的除法(共1小题)
4.(2022•徐州)下列计算正确的是( )
A.a2•a6=a8 B.a8÷a4=a2
C.2a2+3a2=6a4 D.(﹣3a)2=﹣9a2
【答案】A
【解答】解:∵a2•a6=a2+6=a8,
∴A选项的结论符合题意;
∵a8÷a4=a8﹣4=a4,
∴B选项的结论不符合题意;
∵2a2+3a2=5a2,
∴C选项的结论不符合题意;
∵(﹣3a)2=9a2,
∴D选项的结论不符合题意,
故选:A.
五.一元二次方程的应用(共1小题)
5.(2022•南通)李师傅家的超市今年1月盈利3000元,3月盈利3630元.若从1月到3月,每月盈利的平均增长率都相同,则这个平均增长率是( )
A.10.5% B.10% C.20% D.21%
【答案】B
【解答】解:设从1月到3月,每月盈利的平均增长率为x,由题意可得:
3000(1+x)2=3630,
解得:x1=0.1=10%,x2=﹣2.1(舍去),
答:每月盈利的平均增长率为10%.
故答案为:B.
六.一次函数与一元一次不等式(共1小题)
6.(2022•南通)根据图象,可得关于x的不等式kx>﹣x+3的解集是( )
A.x<2 B.x>2 C.x<1 D.x>1
【答案】D
【解答】解:根据图象可知:两函数图象的交点为(1,2),
所以关于x的一元一次不等式kx>﹣x+3的解集为x>1,
故选:D.
七.反比例函数图象上点的坐标特征(共1小题)
7.(2022•无锡)已知一次函数y=x+2的图象上存在两个点,这两个点关于y轴的对称点恰好在反比例函数y=(k>0)的图象上,则k的范围是( )
A.0<k< B.0<k<1 C.0<k<2 D.0<k<4
【答案】B
【解答】解:设一次函数y=x+2的图象上的点坐标为(x,x+2),它关于y轴的对称点坐标为(﹣x,x+2),
根据题意,x+2=有两个解,即x2+2x+k=0有两个不相等的实数根,
∴Δ>0,即22﹣4k>0,
解得k<1,
∵k>0,
∴0<k<1,
故选:B.
八.几何体的展开图(共1小题)
8.(2022•常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
九.专题:正方体相对两个面上的文字(共1小题)
9.(2022•徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
【答案】D
【解答】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、1点6点是相对面,3点与5点是相对面,2点与4点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
B、4点与3点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
C、3点与4点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
D、2点与5点是相对面,3点与4点是相对面,1点与6点是相对面,所以可以折成符合规则的骰子,故本选项符合题意.
故选:D.
一十.平行线的性质(共2小题)
10.(2022•南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是( )
A.30° B.40° C.50° D.80°
【答案】C
【解答】解:如图:
∵a∥b,
∴∠1=∠4,
∵∠3是△ABC的一个外角,
∴∠3=∠4+∠2,
∵∠3=80°,
∴∠1+∠2=80°,
∵∠1﹣∠2=20°,
∴2∠1+∠2﹣∠2=100°,
∴∠1=50°,
故选:C.
11.(2022•盐城)小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
【答案】A
【解答】解:如图,
过点G作GH∥ED,
∵BC∥ED,
∴ED∥GH∥BC,
∴∠ABC=∠AGH,∠DEF=∠HGF,
∵∠HGF+∠AGH=90°,
∴∠ABC+∠DEF=90°
∴∠DEF和∠ABC互余,
故选:A.
一十一.三角形三边关系(共2小题)
12.(2022•淮安)下列长度的三条线段能组成三角形的是( )
A.3,3,6 B.3,5,10 C.4,6,9 D.4,5,9
【答案】C
【解答】解:A、∵3+3=6,
∴长度为3,3,6的三条线段不能组成三角形,本选项不符合题意;
B、∵3+5<10,
∴长度为3,5,10的三条线段不能组成三角形,本选项不符合题意;
C、∵4+6>9,
∴长度为4,6,9的三条线段能组成三角形,本选项符合题意;
D、∵4+5=9,
∴长度为4,5,9的三条线段不能组成三角形,本选项不符合题意;
故选:C.
13.(2022•南通)用一根小木棒与两根长分别为3cm,6cm的小木棒组成三角形,则这根小木棒的长度可以为( )
A.1cm B.2cm C.3cm D.4cm
【答案】D
【解答】解:设第三根木棒长为xcm,由三角形三边关系定理得6﹣3<x<6+3,所以x的取值范围是3<x<9,观察选项,只有选项D符合题意.
故选:D.
一十二.等腰三角形的判定与性质(共1小题)
14.(2022•镇江)如图,点A、B、C、D在网格中小正方形的顶点处,AD与BC相交于点O,小正方形的边长为1,则AO的长等于( )
A.2 B. C. D.
【答案】A
【解答】解:如图:连接AE,
由题意得:
AE∥BC,AD==5,DE=5,
∴AD=DE=5,
∴∠DAE=∠DEA,
∵AE∥BC,
∴∠DAE=∠DOC,∠DEA=∠DCO,
∴∠DOC=∠DCO,
∴DO=DC=3,
∴AO=AD﹣DO=5﹣3=2,
故选:A.
一十三.三角形中位线定理(共1小题)
15.(2022•常州)如图,在△ABC中,D、E分别是AB、AC的中点.若DE=2,则BC的长是( )
A.3 B.4 C.5 D.6
【答案】B
【解答】解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∵DE=2,
∴BC=4,
故选:B.
一十四.矩形的性质(共1小题)
16.(2022•无锡)菱形具有而矩形不一定具有的性质是( )
A.对边平行 B.对角线互相平分
C.对角线互相垂直 D.对角互补
【答案】C
【解答】解:对边平行,对角线互相平分是矩形,菱形都具有的性质,故A,B不符合题意,
对角互补是矩形具有,而菱形不具有的性质,故D不符合题意;
菱形具有而矩形不一定具有的性质是对角线互相垂直,故C符合题意;
故选:C.
一十五.圆内接四边形的性质(共1小题)
17.(2022•淮安)如图,四边形ABCD是⊙O的内接四边形,若∠AOC=160°,则∠ABC的度数是( )
A.80° B.100° C.140° D.160°
【答案】B
【解答】解:∵∠AOC=160°,
∴∠ADC=∠AOC=80°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ABC=180°﹣∠ADC=180°﹣80°=100°,
故选:B.
一十六.切线的性质(共1小题)
18.(2022•无锡)如图,AB是⊙O的直径,AB=6,BC是⊙O的切线,D是AC的中点,OD=2,则AC的值为( )
A.10 B.8 C. D.
【答案】D
【解答】解:∵O为AB中点,D是AC的中点,
∴OD是△ABC的中位线,
∴BC=2OD=2×2=4,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ABC=90°,
∴AC===2,
故选:D.
一十七.相似三角形的判定与性质(共1小题)
19.(2022•徐州)如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )
A.5 B.6 C. D.
【答案】C
【解答】解:∵CD∥AB,
∴△ABE∽△CDE,
∴,
∴,
故选:C.
一十八.相似三角形的应用(共1小题)
20.(2022•盐城)“跳眼法”是指用手指和眼睛估测距离的方法,
步骤:
第一步:水平举起右臂,大拇指紧直向上,大臂与身体垂直;
第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;
第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离的长度;
第四步:将横向距离乘以10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测点的距离值.
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图,该汽车的长度大约为4米,则汽车到观测点的距离约为( )
A.40米 B.60米 C.80米 D.100米
【答案】C
【解答】解:观察图形,横向距离大约是汽车的长度的2倍,
∵汽车的长度大约为4米,
∴横向距离大约是8米,
由“跳眼法”的步骤可知,将横向距离乘以10,得到的值约为被测物体离观测点的距离值,
∴汽车到观测点的距离约为80米,
故选:C.
一十九.折线统计图(共1小题)
21.(2022•徐州)我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率﹣人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
【答案】C
【解答】解:由折线统计图可知,
A.与2012年相比,2021年的人口出生率下降了近一半,说法正确,故本选项不合题意;
B.近十年的人口死亡率基本稳定,说法正确,故本选项不合题意;
C.近五年的人口总数持续下降,说法错误,五年的人口总数增长速度变缓,故本选项符合题意;
D.近五年的人口自然增长率持续下降,说法正确,故本选项不合题意;
故选:C.
二十.加权平均数(共1小题)
22.(2022•无锡)某食堂销售三种午餐盒饭的有关数据如表所示,该食堂销售午餐盒饭的平均价格是( )
品种
A
B
C
单价(元/份)
12
10
8
销售比例
15%
60%
25%
A.10.2元 B.10元 C.9.8元 D.9.5元
【答案】C
【解答】解:∵12×15%+10×60%+8×25%
=1.8+6+2
=9.8(元).
∴该食堂销售午餐盒饭的平均价格为9.8元.
故选:C.
二十一.众数(共1小题)
23.(2022•淮安)某公司对25名营销人员4月份销售某种商品的情况统计如下:
销售量(件)
60
50
40
35
30
20
人数
1
4
4
6
7
3
则这25名营销人员销售量的众数是( )
A.50 B.40 C.35 D.30
【答案】D
【解答】解:因为销售量为30件出现的次数最多,所以这25名营销人员销售量的众数是30.
故选:D.
相关试卷
这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)05解答题基础题②(含解析),共22页。
这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)01选择题容易题①(含解析),共26页。
这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题②,共19页。








