
数学八年级下册16.1 二次根式教案
展开二次根式的性质与化简
一、教学目标
(一)知识与技能:理解二次根式的基本性质,能运用二次根式的性质计算和化简,正确区分![]() (a≥0)和
(a≥0)和![]() (a≥0),了解代数式的概念与特征.
(a≥0),了解代数式的概念与特征.
(二)过程与方法:通过对二次根式的性质的探究,提高学生的思维能力、探究能力、分析问题和解决问题的能力.
(三)情感态度与价值观:通过小组合作学习,经历观察、比较、总结归纳和应用等数学活动,感受数学学习的探索性和创造性,利用小组交流体验发现问题的乐趣,激发学生的学习兴趣,并提高对二次根式性质的应用意识.
二、教学重点、难点
重点:掌握二次根式的性质,会运用其进行有关计算.
难点:二次根式基本性质的应用
三、教学过程
知识回顾
当a>0时,![]() 表示a的算术平方根,因此
表示a的算术平方根,因此![]() >0;当a=0时,
>0;当a=0时,![]() 表示0的算术平方根,因此
表示0的算术平方根,因此![]() =0.这就是说,当 a≥0 时,
=0.这就是说,当 a≥0 时,![]() ≥0.
≥0.
(1)当_____时,![]() 在实数范围内有意义;
在实数范围内有意义;
(2)当x______时,![]() 在实数范围内有意义;
在实数范围内有意义;
(3)已知![]() ,则2x+y=_____.
,则2x+y=_____.
探究
根据算术平方根的意义填空:
![]() ____;
____;![]() ____;
____;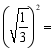 ____;
____;![]() ____.
____.
一般地,![]() (a≥0)
(a≥0)
例2 计算:
(1) ![]() (2)
(2) ![]()
解:(1) ![]() (2)
(2) ![]()
例2(2)用到了(ab)2=a2b2这个结论.(整式的运算性质在实数范围内都适用)
探究
填空:![]() ____;
____;![]() ____;
____;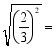 ____;
____;![]() ____.
____.
一般地,根据算术平方根的意义,![]() (a≥0)
(a≥0)
注:![]() (a<0)
(a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值. ![]()
例3 化简:
(1) ![]() (2)
(2) ![]()
解:(1) ![]() =
=![]() =4 (2)
=4 (2) ![]() =
=![]() =5
=5
回顾我们学过的式子,如5,a,a+b,-ab,![]() ,-x3,
,-x3,![]() ,
,![]() (a≥0),它们都是用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式.
(a≥0),它们都是用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式.
判一判
下列哪些是代数式?
(1) 0 (2) n (3) ![]() +5y2 (4) S=πr2 (5) a+b≥2
+5y2 (4) S=πr2 (5) a+b≥2
单独的一个数或一个字母也是代数式;含有等号、不等号的式子不是代数式.
代数式书写格式注意事项:
1.表示数的字母相乘时,可用“· ”代替乘号或省略不写.如:a×b 通常写作a·b或ab.
2.数和字母相乘时,数字应写在字母前面.如: a×2通常写作2a.
3.带分数与字母相乘时,应把带分数化成假分数.如:![]() ×a通常写作
×a通常写作![]() a.
a.
4.含有字母的除式中用分数线代替除号.如:3÷y 通常写作: ![]() .
.
5.最后一步是加、减运算时,如果有单位,要用括号把代数式括起来.如:温度由2℃上升t℃后是(2+t)℃.
练习
1.计算:
(1) ![]() ; (2)
; (2) ![]()
解:(1)原式=3; (2)原式=32×![]() =9×2=18
=9×2=18
2.说出下列各式的值:
(1)![]() ; (2)
; (2) 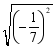 ; (3)
; (3)![]() ; (4)
; (4) ![]() .
.
解:(1)原式=0.3;(2)原式=![]() =
=![]() ;(3)原式=
;(3)原式=![]() =-π;(4)原式=
=-π;(4)原式=![]() =10-1=
=10-1=![]() .
.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
四、教学反思
新的教学理念要求教师在课堂教学中注意引导学生进行探究学习,在课堂教学中,对学生探索求知作出了引导,并且鼓励学生自由发言,但在师生互动方面做得还不够,小组间的合作不够融洽,今后的教学中应多培养学生合作交流的意识,这样有助于他们今后的学习和生活.
人教版16.1 二次根式教案及反思: 这是一份人教版<a href="/sx/tb_c95080_t8/?tag_id=27" target="_blank">16.1 二次根式教案及反思</a>,共5页。
数学第十六章 二次根式16.1 二次根式教学设计: 这是一份数学<a href="/sx/tb_c95080_t8/?tag_id=27" target="_blank">第十六章 二次根式16.1 二次根式教学设计</a>,共8页。教案主要包含了教学目标,教学重,教学过程,教学反思等内容,欢迎下载使用。
初中数学苏科版七年级上册3.4 合并同类项教案设计: 这是一份初中数学苏科版七年级上册3.4 合并同类项教案设计,共2页。












