初中人教版18.1.1 平行四边形的性质教案

这是一份初中人教版18.1.1 平行四边形的性质教案，共3页。教案主要包含了教学目标，教学重点，教学过程，教学反思等内容，欢迎下载使用。
平行四边形的性质(1)一、教学目标(一)知识与技能：理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.(二)过程与方法：会用平行四边形的性质解决简单的平行四边形的计算问题，并会进行有关的论证.(三)情感态度价值观：培养学生发现问题、解决问题的能力及逻辑推理能力.二、教学重点、难点重点：1.理解平行四边形的概念；2.掌握平行四边形边、角的性质.难点：利用平行四边形边、角的性质解决问题.三、教学过程图片欣赏相关概念1.定义：两组对边分别平行的四边形叫做平行四边形.2.记作：□ABCD3.读作：平行四边形ABCD4.对边、对角、对角线5.几何语言：(双重含义)Ⅰ ∵ AB∥CD，AD∥BC，∴ 四边形ABCD是平行四边形Ⅱ ∵ 四边形ABCD是平行四边形，∴ AB∥CD，AD∥BC探究    根据定义画一个平行四边形，观察它，除了“两组对边分别平行”外，它的边之间还有什么关系？它的角之间有什么关系？度量一下，和你的猜想一致吗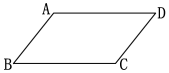？    平行四边形的对边相等；
    平行四边形的对角相等. 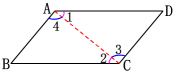已知：四边形ABCD是平行四边形.
求证：AB=CD，BC=DA；∠B=∠D，∠A=∠C. 证明：连接AC
∵ 四边形ABCD是平行四边形
∴ AD∥BC，AB∥CD
∴ ∠1=∠2，∠3=∠4
又 AC是△ABC和△CDA的公共边
∴ △ABC≌△CDA (ASA)
∴ AB=CD，BC=DA，∠B=∠D
又 ∵∠1=∠2，∠3=∠4
∴ ∠1+∠4=∠2+∠3
即 ∠BAD=∠DCB不添加辅助线，你能否直接运用平行四边形的定义，证明其对角相等？证明：
∵ 四边形ABCD是平行四边形
∴ AD∥BC，AB∥CD
∴ ∠B+∠A=180°，∠B+∠C=180°
∴ ∠A=∠C
同理，∠B=∠D形成定理平行四边形性质定理1：平行四边形的对边平行且相等平行四边形性质定理2：平行四边形的对角相等几何符号语言：∵ 四边形ABCD是平行四边形
∴ AB∥CD，AD∥BC，AB=CD，AD=BC，∠A=∠C，∠B=∠D例1 如图，在□ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F. 求证AE=CF.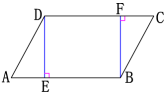证明：∵ 四边形ABCD是平行四边形
∴ ∠A=∠C，AD=CB
∵ DE⊥AB，BF⊥CD
∴ ∠AED=∠CFB=90°
∴ △ADE≌△CBF (AAS)
∴ AE=CF知识回顾1.两点间的距离：连接两点的线段的长度.2.点到直线的距离：直线外一点到这条直线的垂线段的长度.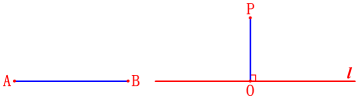 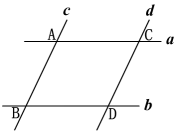   如图，a∥b，c∥d，c，d与a，b分别相交于A，B，C，D四点.由平行四边形的概念和性质可知，四边形ABDC是平行四边形，AB=CD.也就是说，两条平行线之间的任何两条平行线段都相等.  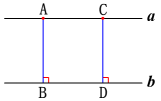         如果两条直线平行，那么一条直线上所有的点到另一条直线的距离都相等.     两条平行线中，一条直线上任意一点到另一条直线的距离，叫做两条平行线间的距离.两条平行线间的距离处处相等.    两条平行线间的距离与点与点之间的距离，点到直线的距离有何联系与区别？练习1.在□ABCD中，(1)已知AB=5，BC=3，求它的周长；(2)已知∠A=38°，求其余各内角的度数.解：(1)□ABCD的周长为：5+5+3+3=16； (2)∠B=142°，∠C=38°，∠D=142°.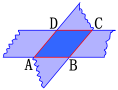2.如图，剪两张对边平行的的纸条，随意交叉叠放在一起，重合的部分构成了一个四边形.转动其中一张纸条，线段AD和BC的长度有什么关系？为什么？解：AD=BC.
理由：两条平行线之间的任何两条平行线段都相等.课堂小结1.本节课你有哪些收获？2.还有没解决的问题吗？四、教学反思学生通过观看多媒体课件的演示和动手操作的过程，得出并掌握平行四边形的性质，效果比较好. 例题能够引导学生用不同的方法去解决问题并加以变式练习，使教师能根据学生的掌握情况及时解决学生在练习的过程中发现问题，并指出错误，规范说理过程，极大提高课堂效率.