人教版八年级下册18.2.1 矩形教案

矩形的性质

一、教学目标

(一)知识与技能：理解矩形的概念，掌握矩形的性质定理，能运用它进行有关的证明和计算.

(二)过程与方法：经历从平行四边形到矩形的研究过程，体验“从一般到特殊”的研究方法，知道矩形与平行四边形的关系.

(三)情感态度价值观：通过动手操作、观察比较、合作交流，激发学生的学习兴趣，体验探索与创造的快乐，感受数学的严谨性，体会数学的美.

二、教学重点、难点

重点：理解并掌握矩形的性质定理及推论，会用矩形的性质定理及推论进行推导证明.

难点：会综合运用矩形的性质定理、推论以及特殊三角形的性质进行证明与计算.

三、教学过程

知识回顾

平行四边形的定义，及其边，角，对角线都有哪些性质呢？

定义：有两组对边分别平行的四边形是平行四边形.

两组对边分别平行；即：AD∥BC，AB∥CD

对边相等；即：AB=DC，AD=BC

对角相等；即：∠DAB=∠BCD，∠ABC=∠CDA

对角线互相平分.即：AO=CO，BO=DO

矩形

    现在来看一个平行四边形，当它的一个内角由锐角变为钝角的过程中，会发生怎样的特殊情况.这时的图形是什么图形呢？

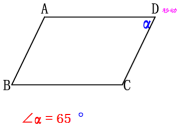
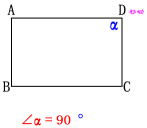
    有一个角是直角的平行四边形叫做矩形，也就是长方形.

探究

    如图，在平行四边形的活动框架上，用橡皮筋做出两条对角线，改变这个平行四边形的形状.随着∠α的变化，两条对角线的长度怎样变化？当∠α变为直角时，平行四边形成为一个矩形，这时它的其它内角是什么样的角？它的两条对角线有什么关系？

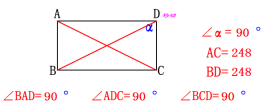
作为特殊的平行四边形，矩形具有平行四边形的所有性质，另外，矩形还有以下性质：
矩形的四个角都是直角；
矩形的对角线相等.

几何符号语言：

∵ 四边形ABCD是矩形

∴ ∠BAD=∠ABC=∠BCD=∠ADC=90°，AC=BD

你能证明矩形的这两个性质吗？

求证：矩形的对角线相等.

已知：如图，四边形ABCD是矩形.求证：AC=BD.

证明：∵ 四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°
又∵ AB=DC，BC=CB
∴ △ABC≌△DCB (SAS)
∴ AC=BD
即 矩形的对角线相等

思考

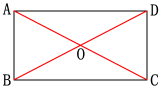
    如图，矩形ABCD的对角线AC，BD相交于点O.我们观察Rt△ABC，在Rt△ABC中，BO是斜边AC上的中线，BO与AC有什么关系？

BO=BD=AC

直角三角形斜边上的中线等于斜边的一半.

几何符号语言：

∵ 在Rt△ABC中，OA=OC
∴ OB=AC.

例1 如图，矩形ABCD的对角线AC，BD相交于点O，∠AOB=60°，AB=4.求矩形对角线的长.

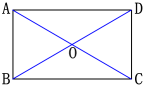解：∵ 四边形ABCD是矩形
∴ AC与BD相等且互相平分
∴ OA=OB
又 ∠AOB=60°
∴ △OAB是等边三角形
∴ OA=AB=4
∴ AC=BD=2OA=8

练习

1.一个矩形的一条对角线长为8，两条对角线的一个交角为120°，求这个矩形的边长(结果保留小数点后两位).

解：∵ 四边形ABCD是矩形
∴ AC与BD相等且互相平分
∴ OA=OB=OC= ×AC=×8=4
∵ ∠AOD=120°，∴ ∠AOB=60°
∴ △OAB是等边三角形
∴ AB=OA=4
又 ∠ABC=90°
∴ 在Rt△ABC中，BC===≈6.93
∴ 矩形的边长分别是4和6.93

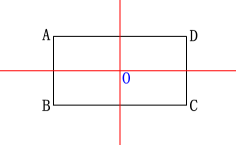
2.矩形是轴对称图形吗？如果是，它有几条对称轴？

解：矩形是轴对称图形，它有两条对称轴.

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

通过多媒体演示知识的探究过程，让学生在体验、实践的过程中有更直观地认识，扩大认知结构，发展能力，更好地理解平行四边形与矩形之间的从属关系和内在联系，使课堂教学真正落实到学生的发展上.