初中数学人教版八年级下册19.1.2 函数的图象教学设计

这是一份初中数学人教版八年级下册19.1.2 函数的图象教学设计，共4页。教案主要包含了教学目标，教学重点，教学过程，教学反思等内容，欢迎下载使用。
函数的图象(1)一、教学目标(一)知识与技能：1.学会用列表、描点、连线画函数图象；2.提高识图能力分析函数图象信息能力.(二)过程与方法：学会观察、分析函数图象信息，体会数形结合思想，并利用它解决问题，提高解诀问题能力.(三)情感态度与价值观：学生在充分经历自学、探究、交流、当堂练习等活动中，获得成功的体验，调动主动学习的积极性，感受数学学习的乐趣.二、教学重点、难点重点：1.函数图象的画法；2.观察分析图象信息.难点：能够结合实际情境，从函数图象中获取信息并处理信息.三、教学过程创设情境你坐过摩天轮吗？你坐在摩天轮上时，随着时间的变化，你离开地面的高度是如何变化的？下图反应旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系.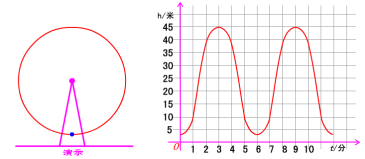有些问题中的函数关系很难列式子表示，但是可以用图来直观地反映.即使对于能列式表示的函数关系，如果也能画图表示，那么会使函数关系更直观.
    例如，正方形的面积S与边长x的函数解析式为S=x2.根据问题的实际意义，可知自变量x的取值范围是x＞0.我们还可以利用在坐标系中画图的方法来表示S与x的关系.
    计算并填写下表：自变量x的一个确定的值与它所对应的唯一的函数值S，是否确定了一个点(x，S)呢？在直角从标系中，画出上面表格中各对数值所对应的点，然后连
接这些点. 所得曲线上每一个点代表x的值与S的值的一种对应，例如点(2，4)表示当x=2时，S=4.表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点，同时想象出其他点的位置.一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象. 如左图的曲线即函数S=x2   (x＞0)的图象.思考下图是自动测温仪记录的图象，它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.你从图象中得到了哪些信息？ 可以认为，气温 T 是时间 t 的函数，上图是这个函数的图象.  例2 如图(1)所示，小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐，接着去图书馆读报，然后回家.图(2)反映了这个过程中，小明离家的距离 y 与时间 x 之间的对应关系.根据图象回答下列问题：(1)食堂离小明家多远？小明从家到食堂用了多少时间？(2)小明吃早餐用了多少时间？(3)食堂离图书馆多远？小明从食堂到图书馆用了多少时间？(4)小明读报用了多少时间？(5)图书馆离小明家多远？小明从图书馆回家的平均速度是多少？解：(1)由纵坐标看出，食堂离小明家0.6km；由横坐标看出，小明到食堂用了8min.(2)由横坐标看出，25-8=17，小明吃早餐用了17min.(3)由纵坐标看出，0.8-0.6=0.2，食堂离图书馆0.2km；由横坐标看出，28-25=3，小明从食堂到图书馆用了3min.(4)由横坐标看出，58-28=30，小明读报用了30min.(5)由纵坐标看出，图书馆离小明家0.8km；由横坐标看出，68-58=10，小明从图书馆回家用了10min，由此算出平均速度是0.08km/min.例3 在下列式子中，对于x的每一个确定的值，y有唯一的对应值，即y是x的函数.画出这些函数的图象：(1) y=x+0.5(1)解：Ⅰ.列表：Ⅱ.描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点. Ⅲ.连线：把这些点用平滑曲线连接起来，就得到y=x+0.5的图象，它是一条直线.从函数图象可以看出，直线从左向右上升，即当x由小变大时，y=x+0.5随之增大.(2) y=(x＞0) 解：Ⅰ.列表：  Ⅱ.描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点.Ⅲ.连线：把这些点用平滑曲线连接起来，就得到y=(x＞0)的图象，它是一条曲线.从函数图象可以看出，曲线从左向右下降，即当x由小变大时，y=(x＞0)随之减小.归纳描点法画函数图象的一般步骤如下：第一步：列表——表中给出一些自变量的值及其对应的函数值；第二步：描点——在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点；第三步：连线——按照横坐标由小到大的顺序，把所描出的各点用平滑曲线连接起来.练习1.(1)画出函数y=2x-1的图象；
(2)判断A(-2.5，-4)，B(1，3)，C(2.5，4)是否在函数y=2x-1的图象上.解：(1)函数y=2x-1的图象如右图所示.(2)∵ 2×(-2.5)-1≠-4
      2×1-1≠3
     2×2.5-1＝4 ∴ 点A，B不在函数y=2x-1的图象上，点C在函数y=2x-1的图象上.2.如图是某一天北京与上海的气温随时间变化的图象.
(1)这一天内，上海与北京何时气温相同？
(2)这一天内，上海在哪段时间比北京气温高？在哪段时间比北京气温低？3.(1)画出函数y=x2的图象.
(2)从图象中观察，当x＜0时，y随x的增大而增大，还是y随x的增大而减小？当x＞0时呢？解：(1)画函数y=x2的图象.(列表、描点、连线) Ⅰ.列表Ⅱ.在直角坐标系中描点.Ⅲ.用平滑的曲线连接各点，便得到函数y=x2的图象.(2)当x＜0时，y随着x的增大而减小；当x＞0时，y随着x的增大而增大.课堂小结1.本节课你有哪些收获？2.还有没解决的问题吗？四、教学反思    本课设计的学习内容都是学生所熟知的事情，情景导入是由实例入手，这些内容有利于学生联系实际，主动进行观察、实验、猜测、验证、推理与交流等数学活动. 通过一些现实生活中用图象来反映的问题实例，让学生经历将实际问题抽象为数学问题的过程. 教学生如何观察分析图象，学会观察图象的一般步骤，利用问题串的形式引导学生逐步深入获得图象所传达的信息，逐步熟悉图象语言.