北师大版八年级下册1 等腰三角形集体备课ppt课件

这是一份北师大版八年级下册1 等腰三角形集体备课ppt课件，共20页。PPT课件主要包含了学习目标，复习导入，什么是等腰三角形，探究新知，证明得到定理，做一做，议一议，典例精析，课堂练习，课堂小结等内容，欢迎下载使用。

1．经历“探索—发现—猜想—证明”的过程，逐步掌握综合法证明的方法，发展推理能力.2．进一步了解作为证明基础的几条基本事实的内容.3．能证明等腰三角形的性质.
8条基本事实具体内容为：1.两点确定一条直线.2.两点之间线段最短.3.同一平面内，过一点有且只有一条直线与已知直线垂直.4.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行（简述为：同位角相等，两直线平行）.5.过直线外一点有且只有一条直线与这条直线平行.6.两边及其夹角分别相等的两个三角形全等.7.两角及其夹边分别相等的两个三角形全等.8.三边分别相等的两个三角形全等.
相等的两边AB，AC都叫做腰，另外一边BC叫做底边，两腰的夹角∠A叫做顶角，腰和底边的夹角∠B，∠C叫做底角．
两角分别相等且其中一组等角的对边相等的两个三角形全等
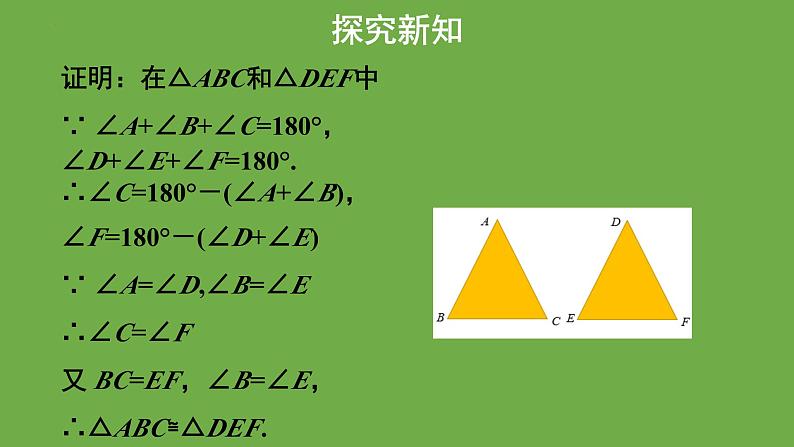
已知：如图，在△ABC和△DEF中，∠A=∠D,∠B=∠E,BC=EF.求证：△ABC≌△DEF.
证明：在△ABC和△DEF中∵ ∠A+∠B+∠C=180°，∠D+∠E+∠F=180°.∴∠C=180°－(∠A+∠B)，∠F=180°－(∠D+∠E)∵ ∠A=∠D,∠B=∠E∴∠C=∠F又 BC=EF，∠B=∠E，∴△ABC≌△DEF.
两角分别相等且其中一组等角的对边相等的两个三角形全等（AAS)
全等三角形的对应边相等，对应角相等
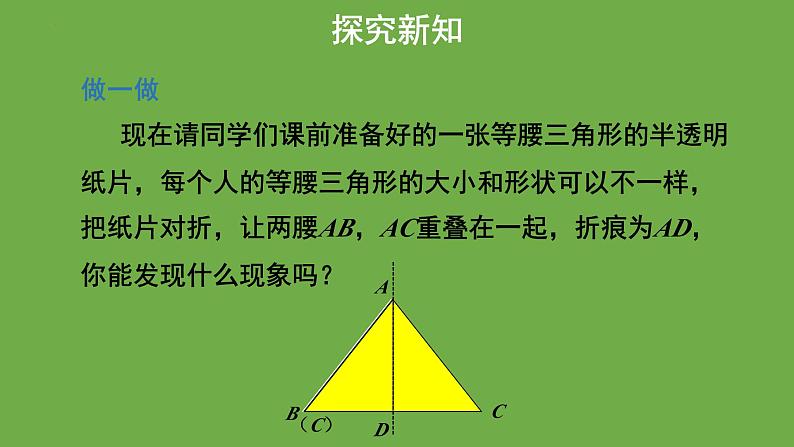
现在请同学们课前准备好的一张等腰三角形的半透明纸片，每个人的等腰三角形的大小和形状可以不一样，把纸片对折，让两腰AB，AC重叠在一起，折痕为AD，你能发现什么现象吗？
曾经探索过等腰三角形的哪些性质？
等腰三角形的两底角相等.(简述为：等边对等角）
等腰三角形的顶角平分线，底边上的高和底边上的中线互相重合 (简称“三线合一”)
已知：如图，在△ABC中，AB=AC.求证：∠B=∠C.
证明：如图，取BC 的中点D，连接AD.∵ AB=AC，BD=CD,AD=AD.∴△ABD≌△ACD(SSS).∴∠B=∠C(全等三角形对应角相等）.
已知：如图，在△ABC中，AB=AC,取BC 的中点D，连接AD.求证：∠ADB＝∠ADC＝90°，∠BAD＝∠CAD．证明：由△ABD≌△ACD可知，∠BAD＝∠CAD，∠ADB＝∠ADC＝90°.
例1 已知：在△ABC中，AB＝AC，∠B＝80°，求∠C和∠A的度数．
∵在△ABC中，AB＝AC，∠B＝80°，∴∠C＝∠B＝80°∠A=180°-(∠B+∠C)＝20°∴∠C＝80°，∠A＝20°．
例2 如图，已知：在△ABC中，AB＝AC，∠A＝30°，BD是△ABC的角平分线，求∠ADB的度数．
解：由AB＝AC，∠A＝30°，得∠ABC＝∠C= ×（180°-30°）=75°，又∵BD是△ABC的角平分线，∴∠ABD＝ ∠ABC= ×75°=37.5°，∴∠ADB=180°-30°-37.5°=112.5°．
1．等腰三角形中的一个角等于100°，则另两个内角的度数分别为（ 　）A．40°，40° 　　　B．100°，20° C．50°，50° 　　　　D．40°，40°或100°，20° 2. 如果一个等腰三角形的一个底角比顶角大15°，那么顶角为（ ）A．45°　　　 B．40° 　 C．55° 　　 D．50°
3．等腰三角形一腰上的高与底边所成的角等于（　 ）A．顶角 　 B．顶角的一半 　　　C．顶角的2倍 　　D．底角的一半4．已知△ABC 的周长为36cm，且AB＝AC，又AD⊥BC，D为垂足，△ABD的周长为30cm，那么AD的长为（ 　 ）A．6cm 　 B．8cm 　　 C．12cm 　 D．20cm
5．如图，已知AB＝AC ＝ BD，那么（　  ）
A．∠1=∠2 　　 B．2∠1+∠2=180° C．∠1+3∠2=180° D．3∠1-∠2=180°
6．如图，在△ABC中，D是AC上的一点，且AD=BD=BC，∠DBC=40° ，则∠A=_______，∠C=______，∠ABC =________．
7．有一个角为20°的等腰三角形的另外两个角的度数分别为 ．
8．如图，在△ABC中，∠B=∠C，点D，E分别在BC，AC边上，∠CDE=15°，且∠AED=∠ADE，求∠BAD的度数．
140°，20°或80°，80°
解：∵在△ABD中，∠BAD=180°﹣∠B﹣∠ADB，∠ADB=180°﹣∠ADC，∴∠BAD=∠ADC﹣∠B，∵∠B=∠C，∠CDE=15°，且∠AED=∠ADE，∴∠BAD=∠ADE+15°﹣∠B =∠B+15°+15°﹣∠B =30°．
1．等腰三角形的两个底角相等(简写成“等边对等角”)．2．等腰三角形的顶角平分线，底边上的高和底边上的中线互相重合 (简称“三线合一”)．