北师大版八年级上册3 一次函数的图象课后复习题

这是一份北师大版八年级上册3 一次函数的图象课后复习题，共8页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。
2023年北师大版数学八年级上册《一次函数的图象》课时练习一              、选择题1.若某正比例函数过(2,－3)，则关于此函数的叙述不正确的是(    ).A.函数值随自变量x的增大而增大B.函数值随自变量x的增大而减小C.函数图象关于原点对称D.函数图象过二、四象限2.经过以下一组点可以画出函数y=2x图象的是(    )A.(0,0)和(2,1)    B.(1,2)和(－1,－2) C.(1,2)和(2,1)    D.(－1,2)和(1,2)3.一次函数y＝(m﹣2)x＋(m﹣1)的图象如图所示，则m的取值范围是(　　)A.m＜2        B.1＜m＜2        C.m＜1        D.m＞24.经过一、二、四象限的函数是(       )A.y＝7         B.y＝﹣2x              C.y＝7﹣2x          D.y＝﹣2x﹣75.若一次函数y=ax+b的图象经过第一、二、四象限，则下列不等式中总是成立的是(  ) A.ab＞0      B.a﹣b＞0        C.a2+b＞0      D.a+b＞06.已知点A(m，﹣3)和点B(n，3)都在直线y＝﹣2x+b上，则m与n的大小关系为(　　)A.m＞n        B.m＜n        C.m＝n        D.大小关系无法确定7.关于直线l：y＝kx＋k(k≠0)，下列说法不正确的是(　　)A.点(0，k)在l上B.l经过定点(－1，0)C.当k＞0时，y随x的增大而增大D.l经过第一、二、三象限8.如图，已知长方形ABCD顶点坐标为A(1，1)，B(3，1)，C(3，4)，D(1，4)，一次函数y＝2x+b的图象与长方形ABCD的边有公共点，则b的变化范围是(　　)A.b≤﹣2或b≥﹣1     B.b≤﹣5或b≥2     C.﹣2≤b≤﹣1      D.﹣5≤b≤2二              、填空题9.若正比例函数y＝(m﹣2)x∣m∣﹣2的图象在第一、三象限内，则m＝_______．10.一次函数y＝﹣3x＋2的图象不经过第　 　象限.11.直线y＝x＋4与x轴、y轴所围成的三角形的面积为________.12.将直线y＝2x﹣1向上平移5个单位长度后再向左平移3个单位后所得的直线解析式是　 　.13.如图，函数y1＝﹣2x与y2＝ax＋3的图象相交于点A(m，2)，则关于x的不等式﹣2x＞ax＋3的解集是　    　.14.如图，直线y＝-x与y＝ax＋3a(a≠0)的交点的横坐标为-1.5，则关于x的不等式-x＞ax＋3a＞0的整数解为________.三              、解答题15.已知y+4与x成正比例，且x=6时，y=8．(1)求出y与x之间的函数关系式；(2)在所给的直角坐标系(如图)中画出函数的图象；(3)直接写出当-4≤y≤0时，自变量x的取值范围．   16.如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，求：(1)一次函数的解析式；(2)△AOC的面积.    17.已知一次函数y＝kx＋b(k≠0)图象过点(0，2)，且与两坐标轴围成的三角形面积为2，求此一次函数的解析式.       18.作出函数y=2﹣x的图象，根据图象回答下列问题：(1)y的值随x的增大而     ；(2)图象与x轴的交点坐标是     ；与y轴的交点坐标是     ； (3)当x     时，y≥0；(4)该函数的图象与坐标轴所围成的三角形的面积是多少？       19.将一次函数y＝kx+4(k≠0)的图象称为直线l．(1)若直线l经过点(2，0)，直接写出关于x的不等式kx+4＞0的解集；(2)若直线l经过点(3，﹣2)，求这个函数的表达式；(3)若将直线l向右平移2个单位长度后经过点(5，5)，求k的值．              20.把函数y＝2x的图象分别沿y轴向上或向下平移3个单位长度，就得到函数y＝2x＋3或y＝2x﹣3的图象.【阅读理解】小尧阅读这段文字后有个疑问：把函数y＝﹣2x的图象沿x轴向右平移3个单位长度，如何求平移后的函数表达式？老师给了以下提示：如图1，在函数y＝﹣2x的图象上任意取两个点A、B，分别向右平移3个单位长度，得到A′、B′，直线A′B′就是函数y＝﹣2x的图象沿x轴向右平移3个单位长度后得到的图象.请你帮助小尧解决他的困难.(1)将函数y＝﹣2x的图象沿x轴向右平移3个单位长度，平移后的函数表达式为　 　.A.y＝﹣2x＋3；    B.y＝﹣2x﹣3；    C.y＝﹣2x＋6；    D.y＝﹣2x﹣6【解决问题】(2)已知一次函数的图象与直线y＝﹣2x关于x轴对称，求此一次函数的表达式.【拓展探究】(3)一次函数y＝﹣2x的图象绕点(2，3)逆时针方向旋转90°后得到的图象对应的函数表达式为　     　.(直接写结果)
答案1.A2.B3.B4.C5.C6.A.7.D.8.D9.答案为：3.10.答案为：三11.答案为：812.答案为：y＝2x＋10.13.答案为：x＜﹣1.14.答案为：﹣2.15.解：(1)∵y＋4与x成正比例，∴设y＋4＝kx(k≠0)．∵当x＝6时，y＝8，∴8＋4＝6k，解得：k＝2，∴y＋4＝2x，∴函数关系式为：y＝2x﹣4；(2)当x＝0时，y＝﹣4，当y＝0时，2x﹣4＝0，解得：x＝2，所以，函数图象经过点(0，﹣4)，(2，0)，函数图象如图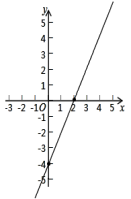：(3)由图象得：当﹣4≤y≤0时，自变量x的取值范围是：0≤x≤2．16.解：(1)∵由图可知A(2，4)、B(0，2)，∴，解得，故此一次函数的解析式为：y=x+2；(2)∵由图可知，C(﹣2，0)，A(2，4)，∴OC=2，AD=4，∴S△AOC=OC•AD=×2×4=4.答：△AOC的面积是4.17.解:∵一次函数y＝kx＋b(k≠0)图象过点(0，2)，∴b＝2.令y＝0，则x＝－.∵函数图象与两坐标轴围成的三角形面积为2，∴×2×|－|＝2，即||＝2，当k＞0时，＝2，解得k＝1；当k＜0时，－＝2，解得k＝－1.故此函数的解析式为：y＝x＋2或y＝－x＋2.18.解：令x=0，y=2；令y=0，x=2，得到(2，0)，(0，2)，描出并连接这两个点，如图，(1)由图象可得，y随x的增大而减小；(2)由图象可得图象与x轴的交点坐标是(2，0)，与y轴交点的坐标是(0，2)；(3)观察图象得，当x≤2时，y≥0，(4)图象与坐标轴围成的三角形的面积为0.5×2×2=2；19.解：(1)不等式kx+4＞0的解集为：x＜2；                (2)将(3，﹣2)代入到y＝kx+4中，3k+4＝﹣2，解得：k＝﹣2．∴函数表达式为y＝﹣2x+4；(3)将点(5，5)向左平移2个单位，得(3，5)，则y＝kx+4的图象经过点(3，5)，将(3，5)代入，解得k＝．20.解：(1)将函数y＝﹣2x的图象沿x轴向右平移3个单位长度，平移后的函数表达式为y＝﹣2x＋6，故选C；(2)在函数y＝﹣2x的图象上取两个点A(0，0)、B(1，﹣2)，关于x轴对称的点的坐标A′(0，0)、B′(1，2)，一次函数的表达式为y＝2x；(3)∵一次函数y＝﹣2x的图象绕点(2，3)逆时针方向旋转90°，∴旋转后得到的图象与原图象垂直，则对应的函数解析式为：y＝x﹣.故答案为：y＝x﹣.