北师大版七年级下册5 利用三角形全等测距离教学设计

3.5 利用三角形全等测距离

●教学目标

（一）教学知识点

利用三角形全等解决实际问题.

（二）能力训练要求

1.能利用三角形全等解决实际问题.体会数学与实际生活的联系.

2.能在解决问题的过程中进行有条理的思考和表达.

（三）情感与价值观要求

1.通过生动、有趣、现实的例子来激发学生的学习兴趣.

2.在活动中让学生体会数学来源于实际，又服务于实际.

●教学重点

三角形全等的应用.

●教学难点

三角形全等的应用.

●教学方法

分组讨论法.

●教具准备

投影片三张

第一张：故事及问题（记作投影片§5.7 A）

第二张：想一想（记作投影片§5.7 B）

第三张：叔叔的主意（记作投影片§5.7 C）

●教学过程

Ⅰ.巧设现实情景，引入新课

［师］前面我们学习了全等三角形的性质及判定条件.现在大家来回忆一下：

（1）全等三角形的性质有哪些？

（2）全等三角形的判定条件有哪些？

［生甲］全等三角形的对应边、对应角相等.

［生乙］全等三角形的判定条件有：

边边边、角边角、角角边、边角边.即：三边对应相等的两个三角形全等.

两角和它们的夹边对应相等的两个三角形全等.

两角和其中一角的对边对应相等的两个三角形全等.

两边和它们的夹角对应相等的两个三角形全等.

［师］很好，在生活中也经常应用全等三角形来解决一些问题.下面是一位经历过战争的老人讲述的一个故事.（出示投影片§5.7 A）

在一次战役中，我军阵地与敌军碉堡隔河相望，为了炸掉这个碉堡，需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下，一个战士想出这样一个办法.他面向碉堡的方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部.然后，他转过一个角度，保持刚才的姿态，这时视线落在了自己所在岸的某一点上，接着，他用步测的办法量出自己与那个点的距离，这个距离就是他与碉堡间的距离.

简易图如下：

图5－155

（1）按这个战士的方法，找出教室中与你距离相等的两个点，并通过测量加以验证.

（2）你能解释其中的道理吗？

［师］现在我们来分组活动：按这位战士的方法，找出教室中与你距离相等的两个点.

在活动时，可用一张纸或一个本代替帽檐，先确定好一个目标，再调整“帽檐”，使视线通过“帽檐”望去时恰好落在目标上，然后保持“帽檐”不动，转过一个角度再望出去，视线所落的位置即为第二个目标.最后大家利用步测等方法测出两个目标与你的距离.验证这位战士做法的合理性.

（学生分组活动，教师指导）

［师］同学们找到与你距离相等的两个点了吗？

［生齐声］找到了.

［师］很好，你能解释其中的道理吗？

［生甲］在这里实际应用了三角形的全等的条件及性质.

［生乙］这个问题可用图5－156来表示:

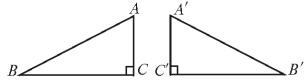
图5－156

AC、A′C′表示某一个人站的位置，点B、点B′分别表示第一目标、第二目标.则：

△ABC≌△A′B′C′BC=B′C′

［师］很好，由此可以看到：这位战士测距离时用到了三角形全等.三角形全等在实际生活中应用较广泛.我们这节课就来研究利用三角形全等测距离.

Ⅱ.讲授新课

［师］下面我们来想一想，做一做（出示投影片§5.7 B）

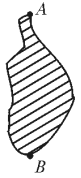
图5－157

如图5－157，A、B两点分别位于一个池塘的两端.小明想用绳子测量A、B间的距离，但绳子不够长，你能帮他想个办法吗？

［师］大家分组来讨论一下.

……

［师］好，看看一位叔叔帮他出的主意（出示投影片§5.7 C）

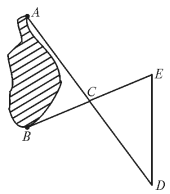
图5－158

如图5－158，先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到D，使CD=AC；连接BC并延长到E，使CE=CB，连接DE并测量出它的长度，DE的长度就是A、B间的距离.

［师］你能说明其中的道理吗？

［生甲］因为AD与BE相交于点C，所以∠ACB与∠DCE是对顶角.从而有∠ACB=∠DCE.又因为CD=AC、CE=CB，所以由“两边及其夹角对应相等的两个三角形全等”可得：△ABC≌△DEC.由“全等三角形的对应边相等”可以得到：AB=DE即DE的长度就是A、B间的距离.

［生乙］还可以用下列格式表明：

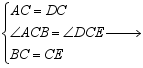△ABC≌△DECAB=DE.

［生丙］如图5－159所示因为有两边及其夹角对应相等，所以：△ABC与△DEC全等，这样AB就等于DE.

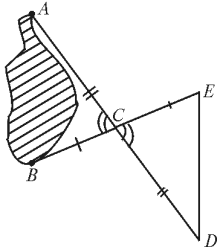
图5－159

［师］同学们解释的理由很清楚.由此我们了解到：要测量无法直接得到的两个点之间的距离时，常常来构造三角形全等.从而得到所要的距离.下面我们来做一练习，以进一步熟悉掌握三角形全等的性质及判定条件.

Ⅲ.课堂练习

（一）课本习题5.12  2

2.我们还有另一种方法可以解决本节的“想一想”中的问题：如图5－160所示：

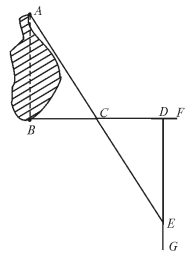
图5－160

要测量A、B间的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再过D点作出BF的垂线DG，并在DG上找一点E，使A，C，E在一条直线上.这时测得的DE的长就是A、B间的距离，你能说出这是为什么吗？

小颖是这样思考的：

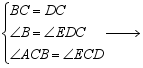△ABC≌△EDCAB=ED.

你知道每一步的理由吗？

答案：（学生用自己的语言叙述理由.）

小颖思考过程每一步的依据是：

两角及其夹边对应相等的两个三角形全等.

全等三角形的对应边相等.

（二）看课本，然后小结.

Ⅳ.课时小结

本节课我们主要利用了三角形的全等解决了实际问题，从中知道了数学与实际生活的联系.

Ⅴ.课后作业

（一）课本习题5.12  1

（二）1.预习后面的内容

2.预习提纲

（1）直角三角形全等的条件是什么？

（2）总结直角三角形全等的条件.

Ⅵ.活动与探究

请你找两个被建筑物隔开的物体，然后想办法测量这两个物体之间的距离.并说明利用什么数学知识.

［过程］通过室外活动，使学生进一步了解利用数学知识来解决实际问题.体会数学与实际生活的联系.

［结果］主要是利用构造三角形全等来测量距离.

●板书设计

3.5  利用三角形全等测距离

一、想一想：

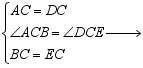△ABC≌△DECAB=DE

二、课堂练习

三、课时小结

四、课后作业