初中数学湘教版七上 1.4.2 第2课时 有理数的加减混合运算课件PPT

这是一份初中数学湘教版七上 1.4.2 第2课时 有理数的加减混合运算课件PPT，共26页。

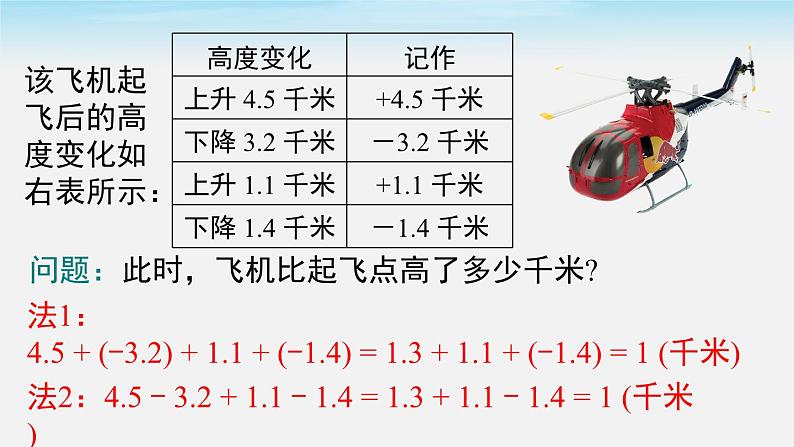
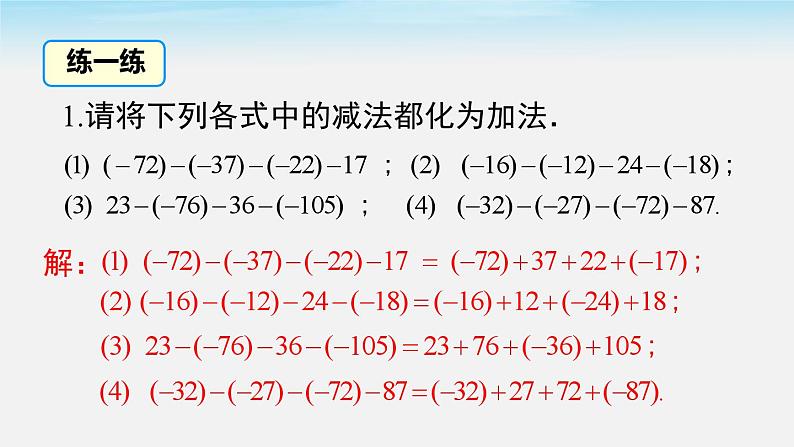
1.4 有理数的加法和减法第1章 有理数第2课时 有理数的加减混合运算1.4.2 有理数的减法 一口深 3.5 米的深井，一只青蛙从井底沿井壁往上爬，第一次爬了 0.7 米又下滑了 0.1米，第二次往上爬了 0.42 米又下滑了 0.15 米，第三次往上爬了 1.25 米又下滑了 0.2 米，第四次往上爬了 0.75 米又下滑了 0.1 米，第五次往上爬了 0.65 米. 问：小青蛙爬出井了吗？观看视频，一架飞机正在作特技表演：该飞机起飞后的高度变化如右表所示：问题：此时，飞机比起飞点高了多少千米? 法1：4.5 + (-3.2) + 1.1 + (-1.4) = 1.3 + 1.1 + (-1.4) = 1 (千米)法2：4.5 - 3.2 + 1.1 - 1.4 = 1.3 + 1.1 - 1.4 = 1 (千米)？省略了加号和括号思考1：比较以上两种方法，你发现了什么？把 4.5－3.2＋1.1－1.4 看作为 4.5，(－3.2)，1.1，(－1.4)的和.所以有两种读法：(1) 看作和式读法：正 4.5、负 3.2、正 1.1、负 1.4 的和；(2) 按运算意义读法：正 4.5 减 3.2 加 1.1 减 1.4.思考2：在前面我们已经学过数的多重符号化简，观察下列式子，你能发现式子中简化符号的规律吗？(－40)－(＋27)＋19－24－(－32)＝－40－27＋19－24＋32(－9)－(－2)＋(－3)－4＝－9 ＋ 2 － 3－4规律：数字前“－”号是奇数个取“－”； 数字前“－”号是偶数个取“＋”．1.请将下列各式中的减法都化为加法．解：注意：和式中第一个加数若是正数，正号也可以省略不写.(-10) + (+2) - (-4) - (+6)问题：把下面的式子的减法化成加法的过程中，你发现了什么？解：原式 = (-10) + (+2)加减混合运算可以统一为加法运算.即 a + b - c = a + b + (- c).转化思想例1 计算：(－2)＋(＋30)－(－15)－(＋27). 解：原式＝(－2)＋(＋30)＋(＋15)＋(－27)＝[(－2)＋(－27)]＋[(＋30)＋(＋15)] ＝(－29)＋(＋45)＝16.减法转化成加法按有理数加法计算方法一：减法变加法典例精析运用了有理数加法的交换律及结合律解：原式＝－2＋30＋15－27＝－2－27＋30＋15＝－29＋45省略括号运用加法交换律使同号两数分别相加＝16.(拓展)方法二：去括号法 去括号法则：对于含有括号的有理数加减混合运算，括号前面是加号时，去掉括号，括号内的算式不变；括号前面是减号时，去掉括号，括号内加号变减号，减号变加号.有理数加减混合运算的步骤：（1）将减法转化为加法运算；（2）省略加号和括号；（3）运用加法交换律和结合律，将同号两数相加；（4）按有理数加法法则计算．归纳总结 例2 计算： （1）-21+30-15-(-17) ； 解：原式 = (-21)+30-15+17 = (-21)+(-15)+30+17 = -36+47 = 11解题小技巧：运用运算律将正负数分别相加.解题小技巧：分母相同或有倍数关系的分数结合相加.解：原式（2）(3) 解题小技巧：在式子中若既有分数又有小数，把小数统一成分数或把分数统一成小数.解：原式= (-0.5)+(+0.25)+(+2.75)+(-5.5) = [(-0.5)+(-5.5)]+(0.25+2.75) = -6+3 = -3解：原式= 解题小技巧：带分数相加减时，可将整数部分和分数部分分开相加，注意分开的时候必须保留原分数的符号.计算：例3 动物园在检验成年麦哲伦企鹅的身体状况时，最重要的一项工作就是称体重.已知某动物园对 6 只成年麦哲伦企鹅进行体重检测，以 4 kg 为标准，超过或者不足的千克数分别用正数、负数表示，称重记录如下表所示，求这 6 只企鹅的总体重. 解：(－0.08)＋(＋0.09)＋(＋0.05)＋(－0.05)＋(＋0.08) ＋(＋0.06) ＝ [(－0.08)＋(＋0.08)]＋[(－0.5)＋0.5]＋(0.09＋0.06) ＝ 0.15. 4×6＋0.15＝24.15.答：这 6 只企鹅的总体重为 24.15 kg.例4 某汽车制造厂计划前半年内每月生产汽车 20 辆，由于另有任务，每月上班人数有变化，1 月至 6 月实际每月生产量和计划每月生产量相比，变化情况如下 (增加为正，减少为负，单位：辆)：＋3，－2，－1，＋4，＋2，－5.(1) 生产量最多的一个月比生产量最少的一个月多生产多少辆？ 解：(＋4)－(－5)＝9(辆)．故生产量最多的一个月比生产量最少的一个月多生产了 9 辆.(2) 前半年的实际总产量是多少？比计划的总产量多了还是少了？相差多少？解：前半年实际总产量为[(＋3)＋(－2)＋(－1)＋(＋4)＋(＋2)＋(－5)]＝＋1(辆)．所以比原计划的总产量多了 1 辆．1. 将式子 3-5-7 写成和的形式，正确的是（　 ） A．3+5+7 B．-3+（-5）+（-7） C．3-（+5）-（+7） D．3+（-5）+（-7）2. 式子 -4 - 2 - 1 + 2 的正确读法是（ ）A．减 4 减 2 减 1 加 2 B．负 4 减 2 减 1 加 2C．-4，-2，-1 加 2 D．4，2，1，2 的和DB解：(1) 原式(2) 原式4. 一批大米，标准质量为每袋 25 kg.质监部门抽取 10袋样品进行检测，把超过标准质量千克数用正数表示，不足的用负数表示，结果如下表： 这 10 袋大米总计质量是多少千克？解：1+(-0.5)+(-1.5)+0.75+(-0.25)+1.5+(-1)+0.5+0+0.5 = [1+(-1)]+[(-0.5)+0.5]+[(-1.5)+1.5]+[(0.75+(-0.25)]+0.5 = 1(kg)， 25×10+1 = 251(kg).答：这 10 袋大米的总计质量是 251 kg.加减混合运算运算律运算方法应用加法交换律：a + b = b + a加法结合律：(a + b) + c = a + (b + c)将加减运算统一写成加法的形式省略加号的和的形式两种读法多个有理数的加减列式计算计算步骤