





所属成套资源:山东省潍坊市2022-2023学年高二下学期期末考试
山东省潍坊市2022-2023学年高二下学期期末考试数学试题
展开
这是一份山东省潍坊市2022-2023学年高二下学期期末考试数学试题,文件包含山东省潍坊市2022-2023学年高二下学期期末数学试题docx、高二数学参考答案及评分标准docx等2份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
![]()
![]() 高二数学2023.7本试卷共4页.满分150分.考试时间120分钟.注意事项:1.答题前,考生务必在试卷、答题卡规定的地方填写自己的准考证号、姓名.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束,考生必须将试卷和答题卡一并交回.一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知等差数列
高二数学2023.7本试卷共4页.满分150分.考试时间120分钟.注意事项:1.答题前,考生务必在试卷、答题卡规定的地方填写自己的准考证号、姓名.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束,考生必须将试卷和答题卡一并交回.一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() A.1 B.2 C.3 D.42.已知直四棱柱的高为1,其底面四边形
A.1 B.2 C.3 D.42.已知直四棱柱的高为1,其底面四边形![]() 水平放置的斜二测直观图为平行四边形
水平放置的斜二测直观图为平行四边形![]() ,
,![]() ,
,![]() ,则该直四棱柱的体积为A.
,则该直四棱柱的体积为A. ![]() B.
B. ![]() C.2 D.43.在空间直角坐标系中,
C.2 D.43.在空间直角坐标系中,![]() 为原点,已知点
为原点,已知点![]() ,
,![]() ,则A.点
,则A.点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() B.点
B.点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() C.点
C.点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() D.点
D.点![]() 关于平面
关于平面![]() 的对称点为
的对称点为![]() 4.已知
4.已知![]() 为正项等比数列,若
为正项等比数列,若![]() ,
,![]() ,则
,则![]() A.6 B.4 C.2 D.
A.6 B.4 C.2 D. ![]() 5.设
5.设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() 是两个不同的平面,则A.若
是两个不同的平面,则A.若![]() ,
,![]() ,
,![]() ,则
,则![]() B.若
B.若![]() ,
,![]() ,
,![]() ,则
,则![]() C.若
C.若![]() ,
,![]() ,
,![]() ,则
,则![]() D.若
D.若![]() ,
,![]() ,
,![]() ,则
,则![]() 6.设
6.设![]() ,
,![]() ,
,![]() ,
,![]() 是各项均不为零的等差数列,且公差
是各项均不为零的等差数列,且公差![]() ,若将此数列删去
,若将此数列删去![]() 得到的新数列(按原来的顺序)是等比数列,则
得到的新数列(按原来的顺序)是等比数列,则![]() 的值为A.
的值为A. ![]() B.
B. ![]() C.
C. ![]() D.-17.若数列
D.-17.若数列![]() 的前
的前![]() 项积
项积![]() ,则
,则![]() 的最大值与最小值的和为A.-3 B.-1 C.2 D.38.如图,在直三棱柱
的最大值与最小值的和为A.-3 B.-1 C.2 D.38.如图,在直三棱柱![]() 中,
中,![]() ,四边形是
,四边形是![]() 边长为1的正方形,
边长为1的正方形,![]() ,
,![]() 是
是![]() 上的一个动点,过点
上的一个动点,过点![]() 作平面
作平面![]() 平面
平面![]() ,记平面
,记平面![]() 截四棱锥
截四棱锥![]() 所得图形的面积为
所得图形的面积为![]() ,平面
,平面![]() 与平面
与平面![]() 之间的距离为
之间的距离为![]() ,则函数
,则函数![]() 的图象大致是
的图象大致是 A.
A. 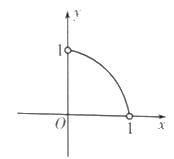 B.
B.  C.
C. 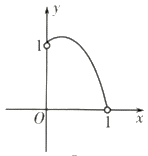 D.
D. 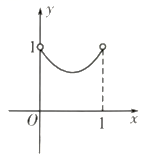 二、多项选择题:本大题共4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.9.已知
二、多项选择题:本大题共4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.9.已知![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() ,则A.数列的公差为-2 B.
,则A.数列的公差为-2 B. ![]() C.
C. ![]() D.数列
D.数列![]() 为递减数列10.已知某圆锥的顶点为
为递减数列10.已知某圆锥的顶点为![]() ,其底面半径为
,其底面半径为![]() ,侧面积为
,侧面积为![]() ,若
,若![]() ,
,![]() 是底面圆周上的两个动点,则A.圆锥的母线长为2 B.圆锥的侧面展开图的圆心角为
是底面圆周上的两个动点,则A.圆锥的母线长为2 B.圆锥的侧面展开图的圆心角为![]() C.
C. ![]() 与圆锥底面所成角的大小为
与圆锥底面所成角的大小为![]() D.
D. ![]() 面积的最大值为
面积的最大值为![]() 11.斐波那契数列又称黄金分割数列,因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为"兔子数列".斐波那契数列用递推的方式可如下定义:用
11.斐波那契数列又称黄金分割数列,因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为"兔子数列".斐波那契数列用递推的方式可如下定义:用![]() 表示斐波那契数列的第
表示斐波那契数列的第![]() 项,则数列
项,则数列![]() 满足:
满足:![]() ,
,![]() ,记
,记![]() 是数列
是数列![]() 的前
的前![]() 项和,则A.
项和,则A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 12.如图,四个半径为2的实心小球两两相切,则
12.如图,四个半径为2的实心小球两两相切,则 A.这四个实心小球所形成的空隙内可以放入一个半径为
A.这四个实心小球所形成的空隙内可以放入一个半径为![]() 的小球B.这四个实心小球所形成的空隙内可以放入一个棱长为
的小球B.这四个实心小球所形成的空隙内可以放入一个棱长为![]() 的正方体C.存在一个侧面积为
的正方体C.存在一个侧面积为![]() 的圆柱可以放进这四个实心小球所形成的空隙内D.这四个实心小球可以放入一个半径为
的圆柱可以放进这四个实心小球所形成的空隙内D.这四个实心小球可以放入一个半径为![]() 的大球内部三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置13.如图,在正方体
的大球内部三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置13.如图,在正方体![]() 中,与
中,与![]() 垂直的面对角线可以是__________.(写出一条即可)
垂直的面对角线可以是__________.(写出一条即可)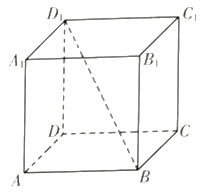 14.已知数列
14.已知数列![]() 满足
满足![]() ,
,![]() ,则
,则![]() __________.15.在四棱锥
__________.15.在四棱锥![]() 中,
中,![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,记直线
,记直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,则
,则![]() ___________
___________![]() (填“>”“<” “≥” “≤”).16.如图,将正整数按下表的规律排列,把行与列交叉处的那个数称为某行某列的元素,记作
(填“>”“<” “≥” “≤”).16.如图,将正整数按下表的规律排列,把行与列交叉处的那个数称为某行某列的元素,记作![]() ,如第2行第4列的数是15,记作
,如第2行第4列的数是15,记作![]() ,则有序数对
,则有序数对![]() 是____________.
是____________.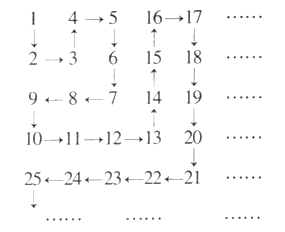 四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤17.(10分)在正三棱柱
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤17.(10分)在正三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() ,
,![]() 分别在棱
分别在棱![]() 和
和![]() 上,且
上,且![]() .(1)证明:四边形
.(1)证明:四边形![]() 为梯形,并求三棱柱
为梯形,并求三棱柱![]() 的表面积;(2)求三棱台
的表面积;(2)求三棱台![]() 的体积.
的体积.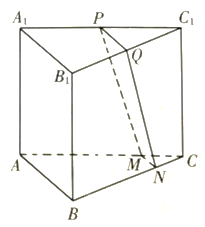 18.(12分)已知递增等比数列
18.(12分)已知递增等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,等差数列
,等差数列![]() 满足
满足![]() ,
,![]() .(1)求数列
.(1)求数列![]() 和
和![]() 的通项公式;(2)若
的通项公式;(2)若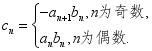 请判断
请判断![]() 与
与![]() 的大小关系,并求数列
的大小关系,并求数列![]() 的前20项和.19.(12分)在如图所示的圆台中,
的前20项和.19.(12分)在如图所示的圆台中,![]() 是下底面圆
是下底面圆![]() 的直径,
的直径,![]() 是上底面圆
是上底面圆![]() 的直径,
的直径,![]() ,
,![]() ,
,![]() ,
,![]() 为圆
为圆![]() 的内接正三角形.(1)证明:
的内接正三角形.(1)证明:![]() 平面
平面![]() ;(2)求直线
;(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.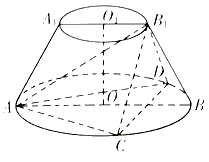 20.(12分)中小微企业是国民经济的重要组成部分,某小微企业准备投入专项资金进行技术创新,以增强自身的竞争力.根据规划,本年度投入专项资金800万元,可实现销售收入40万元;以后每年投入的专项资金是上一年的一半,销售收入比上一年多80万元.同时,当预计投入的专项资金低于20万元时,就按20万元投入,销售收入则与上一年销售收入相等.(1)设第
20.(12分)中小微企业是国民经济的重要组成部分,某小微企业准备投入专项资金进行技术创新,以增强自身的竞争力.根据规划,本年度投入专项资金800万元,可实现销售收入40万元;以后每年投入的专项资金是上一年的一半,销售收入比上一年多80万元.同时,当预计投入的专项资金低于20万元时,就按20万元投入,销售收入则与上一年销售收入相等.(1)设第![]() 年(本年度为第一年)投入的专项资金为
年(本年度为第一年)投入的专项资金为![]() 万元,销售收入为
万元,销售收入为![]() 万元,请写出
万元,请写出![]() ,
,![]() 的表达式;(2)至少要经过多少年后,总销售收入就能超过专项资金的总投入?21.(12分)如图(1),已知四边形
的表达式;(2)至少要经过多少年后,总销售收入就能超过专项资金的总投入?21.(12分)如图(1),已知四边形![]() 是边长为2的正方形,点
是边长为2的正方形,点![]() 在以
在以![]() 为直径的半圆弧上,点
为直径的半圆弧上,点![]() 为
为![]() 的中点.现将半圆沿
的中点.现将半圆沿![]() 折起,如图(2),使异面直线
折起,如图(2),使异面直线![]() 与
与![]() 所成的角为45°,此时
所成的角为45°,此时![]() .(1)证明:
.(1)证明:![]() 平面
平面![]() ,并求点
,并求点![]() 到平面
到平面![]() 的距离;(2)若平面
的距离;(2)若平面![]() 平面
平面![]() ,
,![]() ,当平面
,当平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() 时,求
时,求![]() 的长度.公众号:全元高考
的长度.公众号:全元高考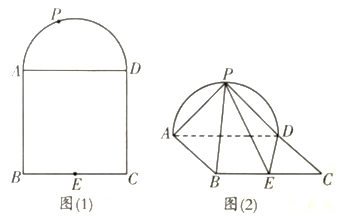 22.(12分)已知正项数列
22.(12分)已知正项数列![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,其中
,其中![]() .(1)证明:数列
.(1)证明:数列![]() 为等比数列;(2)设
为等比数列;(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;(3)记
;(3)记![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,试探究是否存在非零常数
,试探究是否存在非零常数![]() 和
和![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 和
和![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试卷
这是一份山东省潍坊市2022-2023学年高二下学期期末数学试题,共6页。试卷主要包含了已知为正项等比数列,若,,则等内容,欢迎下载使用。
这是一份山东省潍坊市2020-2021学年高二下学期期末考试 数学试题,共10页。
这是一份2022-2023学年山东省潍坊市高二下学期期中数学试题含解析,共17页。试卷主要包含了单选题,多选题,填空题,双空题,解答题等内容,欢迎下载使用。









