湖北省十堰市2021-2023三年中考数学真题分类汇编-01选择题知识点分类

这是一份湖北省十堰市2021-2023三年中考数学真题分类汇编-01选择题知识点分类，共28页。
湖北省十堰市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
一．相反数（共2小题）
1．（2022•十堰）2的相反数是（　　）
A．﹣2 B．2 C．﹣ D．
2．（2022•河南）﹣的相反数是（　　）
A． B．2 C．﹣2 D．﹣
二．倒数（共1小题）
3．（2023•十堰）﹣3的倒数为（　　）
A．3 B． C．﹣ D．﹣3
三．规律型：数字的变化类（共1小题）
4．（2021•十堰）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（　　）

A．2025 B．2023 C．2021 D．2019
四．同底数幂的除法（共1小题）
5．（2022•十堰）下列计算正确的是（　　）
A．a6÷a3＝a2 B．a2+2a2＝3a2
C．（2a）3＝6a3 D．（a+1）2＝a2+1
五．整式的混合运算（共1小题）
6．（2021•十堰）下列计算正确的是（　　）
A．a3•a3＝2a3 B．（﹣2a）2＝4a2
C．（a+b）2＝a2+b2 D．（a+2）（a﹣2）＝a2﹣2
六．二次根式的加减法（共1小题）
7．（2023•十堰）下列计算正确的是（　　）
A．+＝ B．（﹣2a）3＝﹣8a3
C．a8÷a4＝a2 D．（a﹣1）2＝a2﹣1
七．由实际问题抽象出一元一次方程（共1小题）
8．（2022•十堰）我国古代数学名著《张邱建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗．今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？如果设清酒x斗，那么可列方程为（　　）
A．10x+3（5﹣x）＝30 B．3x+10（5﹣x）＝30
C．+＝5 D．+＝5
八．由实际问题抽象出分式方程（共2小题）
9．（2023•十堰）为了落实“双减”政策，进一步丰富文体活动，学校准备购进一批篮球和足球．已知每个篮球的价格比每个足球的价格多20元，用1500元购进篮球的数量比用800元购进足球的数量多5个．如果设每个足球的价格为x元，那么可列方程为（　　）
A． B．
C． D．
10．（2021•十堰）某工厂现在平均每天比原计划多生产50台机器，现在生产400台机器所需时间比原计划生产450台机器所需时间少1天，设现在平均每天生产x台机器，则下列方程正确的是（　　）
A．﹣＝1 B．﹣＝1
C．﹣＝50 D．﹣＝50
九．反比例函数系数k的几何意义（共1小题）
11．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（　　）

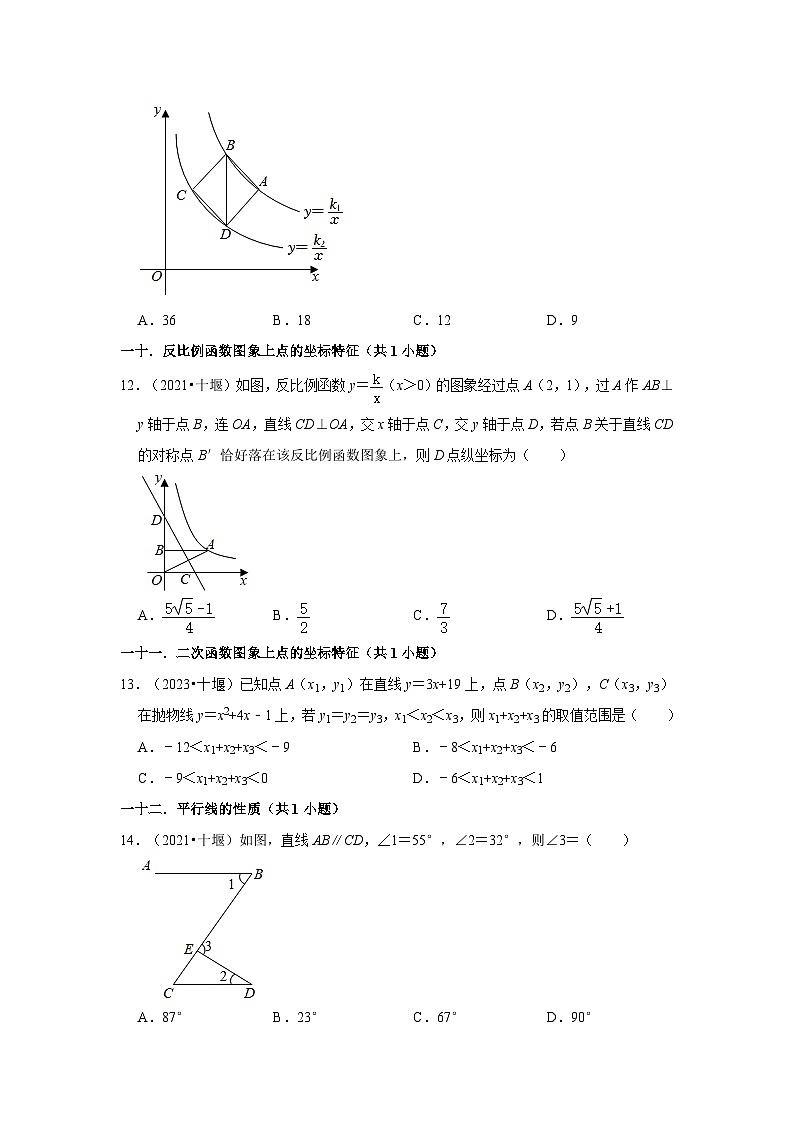
A．36 B．18 C．12 D．9
一十．反比例函数图象上点的坐标特征（共1小题）
12．（2021•十堰）如图，反比例函数y＝（x＞0）的图象经过点A（2，1），过A作AB⊥y轴于点B，连OA，直线CD⊥OA，交x轴于点C，交y轴于点D，若点B关于直线CD的对称点B′恰好落在该反比例函数图象上，则D点纵坐标为（　　）

A． B． C． D．
一十一．二次函数图象上点的坐标特征（共1小题）
13．（2023•十堰）已知点A（x1，y1）在直线y＝3x+19上，点B（x2，y2），C（x3，y3）在抛物线y＝x2+4x﹣1上，若y1＝y2＝y3，x1＜x2＜x3，则x1+x2+x3的取值范围是（　　）
A．﹣12＜x1+x2+x3＜﹣9 B．﹣8＜x1+x2+x3＜﹣6
C．﹣9＜x1+x2+x3＜0 D．﹣6＜x1+x2+x3＜1
一十二．平行线的性质（共1小题）
14．（2021•十堰）如图，直线AB∥CD，∠1＝55°，∠2＝32°，则∠3＝（　　）

A．87° B．23° C．67° D．90°
一十三．三角形三边关系（共1小题）
15．（2022•十堰）如图，工人砌墙时，先在两个墙脚的位置分别插一根木桩，再拉一条直的参照线，就能使砌的砖在一条直线上．这样做应用的数学知识是（　　）

A．两点之间，线段最短
B．两点确定一条直线
C．垂线段最短
D．三角形两边之和大于第三边
一十四．矩形的性质（共1小题）
16．（2023•十堰）如图，将四根木条用钉子钉成一个矩形框架ABCD，然后向左扭动框架，观察所得四边形的变化，下面判断错误的是（　　）

A．四边形ABCD由矩形变为平行四边形
B．对角线BD的长度减小
C．四边形ABCD的面积不变
D．四边形ABCD的周长不变
一十五．三角形的外接圆与外心（共3小题）
17．（2023•十堰）如图，⊙O是△ABC的外接圆，弦BD交AC于点E，AE＝DE，BC＝CE，过点O作OF⊥AC于点F，延长FO交BE于点G，若DE＝3，EG＝2，则AB的长为（　　）

A．4 B．7 C．8 D．
18．（2022•十堰）如图，⊙O是等边△ABC的外接圆，点D是弧AC上一动点（不与A，C重合），下列结论：①∠ADB＝∠BDC；②DA＝DC；③当DB最长时，DB＝2DC；④DA+DC＝DB，其中一定正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个
19．（2021•十堰）如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC，BD是⊙O的直径，若AD＝3，则BC＝（　　）

A．2 B．3 C．3 D．4
一十六．圆锥的计算（共1小题）
20．（2023•十堰）如图，已知点C为圆锥母线SB的中点，AB为底面圆的直径，SB＝6，AB＝4，一只蚂蚁沿着圆锥的侧面从A点爬到C点，则蚂蚁爬行的最短路程为（　　）

A．5 B． C． D．
一十七．相似三角形的应用（共1小题）
21．（2022•十堰）如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果OA：OC＝OB：OD＝3，且量得CD＝3cm，则零件的厚度x为（　　）

A．0.3cm B．0.5cm C．0.7cm D．1cm
一十八．解直角三角形的应用（共1小题）
22．（2021•十堰）如图，小明利用一个锐角是30°的三角板测操场旗杆的高度，已知他与旗杆之间的水平距离BC为15m，AB为1.5m（即小明的眼睛与地面的距离），那么旗杆的高度是（　　）

A．（15+）m B．5m C．15m D．（5+）m
一十九．解直角三角形的应用-坡度坡角问题（共2小题）
23．（2023•十堰）如图所示，有一天桥高AB为5米，BC是通向天桥的斜坡，∠ACB＝45°，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到D处，使∠D＝30°，则CD的长度约为（　　）（参考数据：≈1.414，≈1.732）

A．1.59米 B．2.07米 C．3.55米 D．3.66米
24．（2022•十堰）如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下时，在斜坡上的树影BC长为m，则大树AB的高为（　　）

A．m（cosα﹣sinα） B．m（sinα﹣cosα）
C．m（cosα﹣tanα） D．﹣
二十．简单几何体的三视图（共1小题）
25．（2022•十堰）下列几何体中，主视图与俯视图的形状不一样的几何体是（　　）
A． B．
C． D．
二十一．简单组合体的三视图（共2小题）
26．（2023•十堰）下列几何体中，三视图的三个视图完全相同的几何体是（　　）
A． B．
C． D．
27．（2021•十堰）由5个相同的小立方体搭成的几何体如图所示，则它的俯视图为（　　）

A． B． C． D．
二十二．众数（共1小题）
28．（2021•十堰）某校男子足球队的年龄分布如下表：
年龄
13
14
15
16
17
18
人数
2
6
8
3
2
1
则这些队员年龄的众数和中位数分别是（　　）
A．8，15 B．8，14 C．15，14 D．15，15
二十三．方差（共1小题）
29．（2022•十堰）甲、乙两人在相同的条件下，各射击10次，经计算：甲射击成绩的平均数是8环，方差是1.1；乙射击成绩的平均数是8环，方差是1.5．下列说法中不一定正确的是（　　）
A．甲、乙的总环数相同
B．甲的成绩比乙的成绩稳定
C．乙的成绩比甲的成绩波动大
D．甲、乙成绩的众数相同
二十四．概率公式（共1小题）
30．（2023•十堰）掷一枚质地均匀的正方体骰子，向上一面的点数为偶数的概率是（　　）
A． B． C． D．

湖北省十堰市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
参考答案与试题解析
一．相反数（共2小题）
1．（2022•十堰）2的相反数是（　　）
A．﹣2 B．2 C．﹣ D．
【答案】A
【解答】解：2的相反数等于﹣2．
故选：A．
2．（2022•河南）﹣的相反数是（　　）
A． B．2 C．﹣2 D．﹣
【答案】A
【解答】解：﹣的相反数是，
故选：A．
二．倒数（共1小题）
3．（2023•十堰）﹣3的倒数为（　　）
A．3 B． C．﹣ D．﹣3
【答案】C
【解答】解：﹣3的倒数为﹣．
故选：C．
三．规律型：数字的变化类（共1小题）
4．（2021•十堰）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（　　）

A．2025 B．2023 C．2021 D．2019
【答案】B
【解答】解：由题意可知：
行数为1的方阵内包含“1”，共1个数；
行数为2的方阵内包含“1、3、5、7”，共22个数；
行数为3的方阵内包含“1、3、5、7、9、11、13、15、17”，共32个数；
∴行数为32的方阵内包含“1、3、5、7、......”共322个数，即共1024个数，
∴位于第32行第13列的数是连续奇数的第（1024﹣12）＝1012个数，
∴位于第32行第13列的数是：2×1012﹣1＝2023．
故选：B．
四．同底数幂的除法（共1小题）
5．（2022•十堰）下列计算正确的是（　　）
A．a6÷a3＝a2 B．a2+2a2＝3a2
C．（2a）3＝6a3 D．（a+1）2＝a2+1
【答案】B
【解答】解：A、a6÷a3＝a3，故A不符合题意；
B、a2+2a2＝3a2，故B符合题意；
C、（2a）3＝8a3，故C不符合题意；
D、（a+1）2＝a2+2a+1，故D不符合题意；
故选：B．
五．整式的混合运算（共1小题）
6．（2021•十堰）下列计算正确的是（　　）
A．a3•a3＝2a3 B．（﹣2a）2＝4a2
C．（a+b）2＝a2+b2 D．（a+2）（a﹣2）＝a2﹣2
【答案】B
【解答】解：a3•a3＝a6，故选项A错误；
（﹣2a）2＝4a2，故选项B正确；
（a+b）2＝a2+2ab+b2，故选项C错误；
（a+2）（a﹣2）＝a2﹣4，故选项D错误；
故选：B．
六．二次根式的加减法（共1小题）
7．（2023•十堰）下列计算正确的是（　　）
A．+＝ B．（﹣2a）3＝﹣8a3
C．a8÷a4＝a2 D．（a﹣1）2＝a2﹣1
【答案】B
【解答】解：A．+无法合并，故此选项不合题意；
B．（﹣2a）3＝﹣8a3，故此选项符合题意；
C．a8÷a4＝a4，故此选项不合题意；
D．（a﹣1）2＝a2﹣2a+1，故此选项不合题意．
故选：B．
七．由实际问题抽象出一元一次方程（共1小题）
8．（2022•十堰）我国古代数学名著《张邱建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗．今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？如果设清酒x斗，那么可列方程为（　　）
A．10x+3（5﹣x）＝30 B．3x+10（5﹣x）＝30
C．+＝5 D．+＝5
【答案】A
【解答】解：设清酒x斗，则醑酒（5﹣x）斗，
由题意可得：10x+3（5﹣x）＝30，
故选：A．
八．由实际问题抽象出分式方程（共2小题）
9．（2023•十堰）为了落实“双减”政策，进一步丰富文体活动，学校准备购进一批篮球和足球．已知每个篮球的价格比每个足球的价格多20元，用1500元购进篮球的数量比用800元购进足球的数量多5个．如果设每个足球的价格为x元，那么可列方程为（　　）
A． B．
C． D．
【答案】A
【解答】解：设每个足球的价格为x元，可列方程为：
﹣＝5．
故选：A．
10．（2021•十堰）某工厂现在平均每天比原计划多生产50台机器，现在生产400台机器所需时间比原计划生产450台机器所需时间少1天，设现在平均每天生产x台机器，则下列方程正确的是（　　）
A．﹣＝1 B．﹣＝1
C．﹣＝50 D．﹣＝50
【答案】B
【解答】解：设现在平均每天生产x台机器，则原计划平均每天生产（x﹣50）台机器，
根据题意，得﹣＝1．
故选：B．
九．反比例函数系数k的几何意义（共1小题）
11．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图象上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（　　）

A．36 B．18 C．12 D．9
【答案】B
【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：

∵四边形ABCD是正方形，
∴AE＝BE＝CE＝DE，
设AE＝BE＝CE＝DE＝m，D（3，a），
∵BD∥y轴，
∴B（3，a+2m），A（3+m，a+m），
∵A，B都在反比例函数y＝（k1＞0）的图象上，
∴k1＝3（a+2m）＝（3+m）（a+m），
∵m≠0，
∴m＝3﹣a，
∴B（3，6﹣a），
∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图象上，D（3，a）在y＝（k2＞0）的图象上，
∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，
∴k1+k2＝18﹣3a+3a＝18；
故选：B．
一十．反比例函数图象上点的坐标特征（共1小题）
12．（2021•十堰）如图，反比例函数y＝（x＞0）的图象经过点A（2，1），过A作AB⊥y轴于点B，连OA，直线CD⊥OA，交x轴于点C，交y轴于点D，若点B关于直线CD的对称点B′恰好落在该反比例函数图象上，则D点纵坐标为（　　）

A． B． C． D．
【答案】A
【解答】解：设BB′交直线CD于点E，过点E作EG⊥BD于G，过B′作B′F⊥BD于点F，如图，

∵B与B′关于直线CD对称，
∴CD垂直平分BB′．
即E为BB′的中点，EB＝EB′．
∵EG⊥BD，B′F⊥BD，
∴EG∥B′F．
∴EG＝B′F．
∵直线OA经过点A（2，1），
∴直线OA的解析式为：y＝x．
∵CD⊥OA，BB′⊥CD，
∴BB′∥OA．
设直线BB′的解析式为y＝x+b，
∵B（0，1），
∴b＝1．
∴直线BB′的解析式为y＝x+1．
∵反比例函数y＝（x＞0）的图象经过点A（2，1），
∴反比例函数y＝．
联立方程得：．
解得：，．
∴B′（）．
∴B′F＝．
∴EG＝．
∵AB⊥BD，
∴∠OAB＝∠ODC．
∴tan∠OAB＝tan∠ODC＝．
在Rt△DGE中，
∵tan∠ODC＝，
∴DG＝﹣1．
同理：BG＝．
∴OD＝OB+BG+DG＝．
∴D点纵坐标为．
故选：A．
一十一．二次函数图象上点的坐标特征（共1小题）
13．（2023•十堰）已知点A（x1，y1）在直线y＝3x+19上，点B（x2，y2），C（x3，y3）在抛物线y＝x2+4x﹣1上，若y1＝y2＝y3，x1＜x2＜x3，则x1+x2+x3的取值范围是（　　）
A．﹣12＜x1+x2+x3＜﹣9 B．﹣8＜x1+x2+x3＜﹣6
C．﹣9＜x1+x2+x3＜0 D．﹣6＜x1+x2+x3＜1
【答案】A
【解答】解：令3x+19＝x2+4x﹣1，整理得x2+x﹣20＝0，
解得x1＝﹣5，x2＝4，
∴直线y＝3x+19与抛物线的交点的横坐标为﹣5，4，
∵y＝x2+4x﹣1＝（x+2）2﹣5，
∴抛物线开口向上，对称轴为直线x＝﹣2，顶点为（﹣2，﹣5），
把y＝﹣5代入y＝3x+19，解得x＝﹣8，
若y1＝y2＝y3，x1＜x2＜x3，则﹣8＜x1＜﹣5，x2+x3＝﹣4，
∴﹣12＜x1+x2+x3＜﹣9，
故选：A．
一十二．平行线的性质（共1小题）
14．（2021•十堰）如图，直线AB∥CD，∠1＝55°，∠2＝32°，则∠3＝（　　）

A．87° B．23° C．67° D．90°
【答案】A
【解答】解：∵AB∥CD，∠1＝55°，
∴∠C＝∠1＝55°，
∵∠3＝∠2+∠C，∠2＝32°，
∴∠3＝32°+55°＝87°，
故选：A．
一十三．三角形三边关系（共1小题）
15．（2022•十堰）如图，工人砌墙时，先在两个墙脚的位置分别插一根木桩，再拉一条直的参照线，就能使砌的砖在一条直线上．这样做应用的数学知识是（　　）

A．两点之间，线段最短
B．两点确定一条直线
C．垂线段最短
D．三角形两边之和大于第三边
【答案】B
【解答】解：这样做应用的数学知识是两点确定一条直线，
故选：B．
一十四．矩形的性质（共1小题）
16．（2023•十堰）如图，将四根木条用钉子钉成一个矩形框架ABCD，然后向左扭动框架，观察所得四边形的变化，下面判断错误的是（　　）

A．四边形ABCD由矩形变为平行四边形
B．对角线BD的长度减小
C．四边形ABCD的面积不变
D．四边形ABCD的周长不变
【答案】C
【解答】解：向左扭动矩形框架ABCD，只改变四边形的形状，四边形变成平行四边形，A不符合题意；
此时对角线BD减小，对角线AC增大，B不合题意．
BC边上的高减小，故面积变小，C符合题意，
四边形的四条边不变，故周长不变，D不符合题意．
故选：C．
一十五．三角形的外接圆与外心（共3小题）
17．（2023•十堰）如图，⊙O是△ABC的外接圆，弦BD交AC于点E，AE＝DE，BC＝CE，过点O作OF⊥AC于点F，延长FO交BE于点G，若DE＝3，EG＝2，则AB的长为（　　）

A．4 B．7 C．8 D．
【答案】B
【解答】解：在△AEB和△DEC中，
，
∴△AEB≌△DEC（ASA），
∴EB＝EC，
∵BC＝CE，
∴BE＝CE＝BC，
∴△EBC为等边三角形，
∴∠ACB＝60°，
如图，作BM⊥AC于点M，
∵OF⊥AC，
∴AF＝CF，
∵△EBC为等边三角形，
∴∠GEF＝60°，
∴∠EGF＝30°，
∵EG＝2，
∴EF＝1，
∵AE＝ED＝3，
∴CF＝AF＝4，
∴AC＝8，EC＝5，
∴BC＝5，
∵∠BCM＝60°，
∴∠MBC＝30°，
∴CM＝，BM＝CM＝，
∴AM＝AC﹣CM＝，
∴AB＝＝7．
故选：B．

18．（2022•十堰）如图，⊙O是等边△ABC的外接圆，点D是弧AC上一动点（不与A，C重合），下列结论：①∠ADB＝∠BDC；②DA＝DC；③当DB最长时，DB＝2DC；④DA+DC＝DB，其中一定正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个
【答案】C
【解答】解：∵△ABC是等边三角形，
∴∠BAC＝∠ACB＝60°，
∵＝，＝，
∴∠ADB＝∠ACB＝60°，∠BDC＝∠BAC＝60°，
∴∠ADB＝∠BDC，故①正确；
∵点D是弧AC上一动点，
∴与不一定相等，
∴DA与DC不一定相等，故②错误；
当DB最长时，DB为⊙O直径，
∴∠BCD＝90°，
∵∠BDC＝60°，
∴∠DBC＝30°，
∴DB＝2DC，故③正确；
在DB上取一点E，使DE＝AD，如图：

∵∠ADB＝60°，
∴△ADE是等边三角形，
∴AD＝AE，∠DAE＝60°，
∵∠BAC＝60°，
∴∠BAE＝∠CAD，
∵AB＝AC，
∴△ABE≌△ACD（SAS），
∴BE＝CD，
∴BD＝BE+DE＝CD+AD，故④正确；
∴正确的有①③④，共3个，
故选：C．
19．（2021•十堰）如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC，BD是⊙O的直径，若AD＝3，则BC＝（　　）

A．2 B．3 C．3 D．4
【答案】C
【解答】解：过点O作OE⊥BC于点E，如图所示：

∵∠BAC＝120°，AB＝AC，
∴∠ABC＝∠ACB＝30°，
又∵对应圆周角为∠ACB和∠ADB，
∴∠ACB＝∠ADB＝30°，
而BD为直径，
∴∠BAD＝90°，
在Rt△BAD中，∠ADB＝30°，AD＝3，
∴cos30°＝＝＝，
∴BD＝2，
∴OB＝，
又∵∠ABD＝90°﹣∠ADB＝90°﹣30°＝60°，∠ABC＝30°，
∴∠OBE＝30°，
又∵OE⊥BC，
∴△OBE为直角三角形，
∴cos∠OBE＝cos30°＝＝，
∴BE＝，
由垂径定理可得：BC＝2BE＝2×＝3，故C正确，
故选：C．
一十六．圆锥的计算（共1小题）
20．（2023•十堰）如图，已知点C为圆锥母线SB的中点，AB为底面圆的直径，SB＝6，AB＝4，一只蚂蚁沿着圆锥的侧面从A点爬到C点，则蚂蚁爬行的最短路程为（　　）

A．5 B． C． D．
【答案】B
【解答】解：由题意知，底面圆的直径AB＝4，
故底面周长等于4π，
设圆锥的侧面展开后的扇形圆心角为n°，
根据底面周长等于展开后扇形的弧长得4π＝，
解得n＝120°，
所以展开图中∠ASC＝120°÷2＝60°，
因为半径SA＝SB，∠ASB＝60°，
故三角形SAB为等边三角形，
又∵C为SB的中点，
所以AC⊥SB，在直角三角形SAC中，SA＝6，SC＝3，
根据勾股定理求得AC＝3，
所以蚂蚁爬行的最短距离为3．
故选：B．
一十七．相似三角形的应用（共1小题）
21．（2022•十堰）如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果OA：OC＝OB：OD＝3，且量得CD＝3cm，则零件的厚度x为（　　）

A．0.3cm B．0.5cm C．0.7cm D．1cm
【答案】B
【解答】解：∵OA：OC＝OB：OD＝3，∠COD＝∠AOB，
∴△COD∽△AOB，
∴AB：CD＝3，
∵CD＝3cm，
∴AB＝9cm，
∵某零件的外径为10cm，
∴零件的厚度x为：（10﹣9）÷2＝1÷2＝0.5（cm），
故选：B．
一十八．解直角三角形的应用（共1小题）
22．（2021•十堰）如图，小明利用一个锐角是30°的三角板测操场旗杆的高度，已知他与旗杆之间的水平距离BC为15m，AB为1.5m（即小明的眼睛与地面的距离），那么旗杆的高度是（　　）

A．（15+）m B．5m C．15m D．（5+）m
【答案】D
【解答】解：由题意可得，四边形ABCD是矩形，BC＝15m，AB＝1.5m，
∴BC＝AD＝15m，AB＝CD＝1.5m，
在Rt△ADE中，∠EAD＝30°，AD＝15m，
∴DE＝AD•tan∠EAD＝15×＝5（m），
∴CE＝CD+DE＝（5+1.5）（m）．
故选：D．
一十九．解直角三角形的应用-坡度坡角问题（共2小题）
23．（2023•十堰）如图所示，有一天桥高AB为5米，BC是通向天桥的斜坡，∠ACB＝45°，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到D处，使∠D＝30°，则CD的长度约为（　　）（参考数据：≈1.414，≈1.732）

A．1.59米 B．2.07米 C．3.55米 D．3.66米
【答案】D
【解答】解：在Rt△ABC中，∠BAC＝90°，∠ACB＝45°，
∴∠ABC＝∠ACB＝45°，
∴AC＝AB＝5米，
在Rt△ABD中，∠BAD＝90°，∠D＝30°，
∴∠ABD＝60°，
∴＝tan∠ABD＝tan60°＝，
∴AD＝AB，
∴CD＝AD﹣AC＝AB﹣AC≈1.732×5﹣5≈3.66（米），
∴CD的长度约为3.66米，
故选：D．
24．（2022•十堰）如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下时，在斜坡上的树影BC长为m，则大树AB的高为（　　）

A．m（cosα﹣sinα） B．m（sinα﹣cosα）
C．m（cosα﹣tanα） D．﹣
【答案】A
【解答】解：过点C作水平地面的平行线，交AB的延长线于D，
则∠BCD＝α，
在Rt△BCD中，BC＝m，∠BCD＝α，
则BD＝BC•sin∠BCD＝msinα，CD＝BC•cos∠BCD＝mcosα，
在Rt△ACD中，∠ACD＝45°，
则AD＝CD＝mcosα，
∴AB＝AD﹣BD＝mcosα﹣msinα＝m（cosα﹣sinα），
故选：A．

二十．简单几何体的三视图（共1小题）
25．（2022•十堰）下列几何体中，主视图与俯视图的形状不一样的几何体是（　　）
A． B．
C． D．
【答案】C
【解答】解：A、正方体的主视图与俯视图都是正方形，故A不符合题意；
B、圆柱的主视图与俯视图都是长方形，故B不符合题意；
C、圆锥的主视图是等腰三角形，俯视图是一个圆和圆心，故C符合题意；
D、球体的主视图与俯视图都是圆形，故D不符合题意；
故选：C．
二十一．简单组合体的三视图（共2小题）
26．（2023•十堰）下列几何体中，三视图的三个视图完全相同的几何体是（　　）
A． B．
C． D．
【答案】D
【解答】解：A．长方体的主视图和左视图都是矩形，俯视图是正方形，故不符合题意；
B．圆锥的三视图主视图和左视图都是等腰三角形，俯视图是带圆心的圆，故不符合题意；
C．圆柱的三视图既有圆又有长方形，故不符合题意；
D．球的三视图都是圆，故符合题意；
故选：D．
27．（2021•十堰）由5个相同的小立方体搭成的几何体如图所示，则它的俯视图为（　　）

A． B． C． D．
【答案】A
【解答】解：从上面看，底层有3个正方形，上层右边有一个正方形．
故选：A．
二十二．众数（共1小题）
28．（2021•十堰）某校男子足球队的年龄分布如下表：
年龄
13
14
15
16
17
18
人数
2
6
8
3
2
1
则这些队员年龄的众数和中位数分别是（　　）
A．8，15 B．8，14 C．15，14 D．15，15
【答案】D
【解答】解：根据图表数据，同一年龄人数最多的是15岁，共8人，所以众数是15；
根据图表数据可知共有22名队员，按照年龄从小到大排列，第11名队员与第12名队员的年龄都是15岁，所以，中位数是（15+15）÷2＝15．
故选：D．
二十三．方差（共1小题）
29．（2022•十堰）甲、乙两人在相同的条件下，各射击10次，经计算：甲射击成绩的平均数是8环，方差是1.1；乙射击成绩的平均数是8环，方差是1.5．下列说法中不一定正确的是（　　）
A．甲、乙的总环数相同
B．甲的成绩比乙的成绩稳定
C．乙的成绩比甲的成绩波动大
D．甲、乙成绩的众数相同
【答案】D
【解答】解：∵各射击10次，甲射击成绩的平均数是8环，乙射击成绩的平均数是8环，
∴甲、乙的总环数相同，故A正确，不符合题意；
∵甲射击成绩的方差是1.1；乙射击成绩的方差是1.5，
∴甲的成绩比乙的成绩稳定，乙的成绩比甲的成绩波动大，故B，C都正确，不符合题意；
由已知不能得到甲、乙成绩的众数相同，故D不一定正确，符合题意；
故选：D．
二十四．概率公式（共1小题）
30．（2023•十堰）掷一枚质地均匀的正方体骰子，向上一面的点数为偶数的概率是（　　）
A． B． C． D．
【答案】C
【解答】解：根据题意可得：掷一次骰子，向上一面的点数有6种情况，其中有3种为向上一面的点数偶数，
故其概率是＝．
故选：C．