2024届新高考数学一轮复习资料第4讲：基本不等式导学案+练习

第4讲基本不等式练习

1．下列不等式恒成立的是(　　)

A．a2＋b2≤2ab         B．a2＋b2≥－2ab

C．a＋b≥2      D．a＋b≤－2

2．已知直线ax＋2by－1＝0和x2＋y2＝1相切，则ab的最大值是(　　)

A．     B．     C． D．1

3．（多选）（2020·海南·高考真题）已知a>0，b>0，且a+b=1，则（       ）

A． B．

C． D．

4.(2022·汕头一模)(多选)已知正实数a，b满足a＋2b＝ab，则以下不等式正确的是(　　)

A. ＋≥2  B. a＋2b≥8

C. log2a＋log2b<3  D. 2a＋b≥9

5．（2019·天津·高考真题（文）） 设，，，则的最小值为__________.

6.设k＞0，若关于x的不等式kx＋≥12在(1，＋∞)上恒成立，则k的最小值为____.

7.若则的最小值为_________．

8．当取得最小值时，x＝________.

9．函数f (x)＝ (x＞1)的最小值是________．

10．（2022·全国·模拟预测）已知正数，满足，则的最小值为______．

11．（2022·福建龙岩·模拟预测）若正实数a，b满足，则的最小值为___________.

12.已知某工厂每天固定成本是4万元，每生产一件产品成本增加100元，工厂每件产品的出厂价定为a元时，生产x件产品的销售收入是R(x)＝－x2＋500x(元)，P(x)为每天生产x件产品的平均利润(平均利润＝总利润/总产量)．

销售商从工厂每件a元进货后又以每件b元销售， b＝a＋λ(c－a)，其中c为最高限价(a＜b＜c)，λ为销售乐观系数．据市场调查，λ是由当b－a是c－b，c－a的比例中项时来确定．

(1)每天生产量x为多少时，平均利润P(x)取得最大值？求P(x)的最大值．

(2)求乐观系数λ的值．

(3)若c＝600，当厂家平均利润最大时，求a与b的值．

参考答案

1.【答案】B　

【解析】对于选项A，因为a2＋b2－2ab＝(a－b)2≥0，当且仅当a＝b时取等号，

所以a2＋b2≥2ab，故A错误．

对于选项B，因为a2＋b2＋2ab＝(a＋b)2≥0，当且仅当a＝－b时取等号，

所以a2＋b2≥－2ab，故B正确．

对于选项C，令a＝－1，b＝2，则a＋b＝－1＋2＝1，2＝2＝2.

因为1＜2，所以a＋b＜2，故C错误．

对于选项D，令a＝1，b＝0，则a＋b＝1，－2＝－2＝0.

因为1>0，所以a＋b>－2，故D错误．

2.【答案】A　

【解析】根据题意，圆x2＋y2＝1的圆心为(0,0)，半径r＝1，若直线ax＋2by－1＝0和x2＋y2＝1相切，则有＝1，变形可得a2＋4b2＝1，又由1＝a2＋4b2≥4ab，变形可得ab≤，当且仅当a＝2b时等号成立，故ab的最大值是，故选A．

3.【答案】ABD

【解析】对于A，，

当且仅当时，等号成立，故A正确；

对于B，，所以，故B正确；

对于C，，

当且仅当时，等号成立，故C不正确；

对于D，因为，

所以，当且仅当时，等号成立，故D正确；

故选：ABD

4.【解析】 对于A，因为正实数a，b满足a＋2b＝ab，所以＝1，即＋＝1，所以A错误．对于B，因为a>0，b>0，a＋2b＝ab，所以a＋2b≥2＝2，当且仅当a＝2b时取等号，所以(a＋2b)2≥8(a＋2b)．因为a＋2b>0，所以a＋2b≥8，当且仅当a＝2b时取等号，所以B正确．对于C，若log2a＋log2b<3，则log2a＋log2b＝log2(ab)<3＝log28，所以ab<8，所以a＋2b<8，而由B可知a＋2b≥8，所以log2a＋log2b<3不成立，所以C错误．对于D，因为正实数a，b满足a＋2b＝ab，所以＝1，即＋＝1，所以2a＋b＝(2a＋b)＝5＋＋≥5＋2＝9，当且仅当＝，即a＝b＝3时取等号，所以D正确．

5.【答案】.

【解析】由，得，得

，

等号当且仅当，即时成立．

故所求的最小值为．

6.【解析】 原不等式变形为k(x－1)＋＋k≥12，则原问题转化成不等式k(x－1)＋≥12－k在(1，＋∞)上恒成立，所以只需12－k≤min即可．由基本不等式可知，k(x－1)＋≥2＝4，当且仅当k(x－1)＝时等号成立，所以只需12－k≤4成立，即(＋6)(－2)≥0，所以k≥4，即kmin＝4.

7.【答案】【解析】因为，则，

，

当且仅当，即当时，等号成立，

因此，的最小值为.故答案为：.

8.【答案】4　

【解析】＋＝＋1＋－1≥2－1＝5，当且仅当＋1＝，即x＝4时，等号成立．

9.【答案】2　

【解析】由于x＞1，故x－1＞0，故f (x)＝2(x－1)＋≥2＝2，当且仅当2(x－1)＝，即x＝1＋时，函数取得最小值2.

10.【答案】##

【解析】

，当且仅当，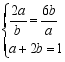

即，时取得等号．故答案为：.

11.【答案】1

【解析】∵，当且仅当时等号成立

即，则

∴或（舍去），即

故答案为：1．

12.【解析】(1)依题意，总利润为－x2＋500x－100x－40 000＝－x2＋400x－40 000，

所以P(x)＝＝－x－＋400

≤－200＋400＝200.当且仅当x＝，即x＝400时取等号，

故每天生产量为400件时，平均利润最大，最大值为200元．

(2)由b＝a＋λ(c－a)得λ＝.

因为b－a是c－b，c－a的比例中项，

所以(b－a)2＝(c－b)(c－a)，

两边除以(b－a)2得，1＝·＝·，

所以1＝·，解得λ＝.

(3)由(1)知，当x＝400时，厂家平均利润最大，

所以a＝＋100＋P(x)＝＋100＋200＝400(元)．

每件产品的利润为b－a＝λ(c－a)＝100(－1)，

所以b＝100(＋3)，

所以a＝400，b＝100(＋3)．