数学九年级上册3.1 比例线段优秀ppt课件

这是一份数学九年级上册3.1 比例线段优秀ppt课件，共29页。PPT课件主要包含了学习目标，做一做，黄金分割的概念，计算黄金比，课堂小结等内容，欢迎下载使用。

1.理解线段的比与成比例线段的关系；（重点、难点）2.了解并掌握黄金分割问题．(重点、难点)
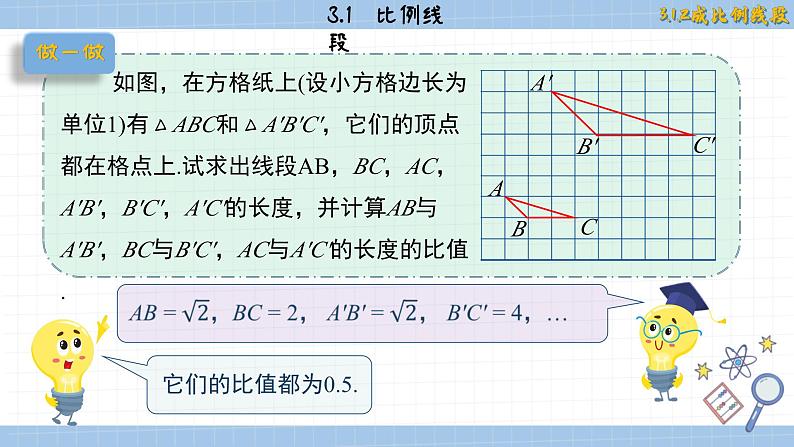
如图，在方格纸上(设小方格边长为单位1)有△ABC和△A′B′C′，它们的顶点都在格点上.试求出线段AB，BC，AC，A′B′，B′C′，A′C′的长度，并计算AB与A′B′，BC与B′C′，AC与A′C′的长度的比值.
一、线段的比和成比例线段
在图中，对于△ABC和△A′B′C′，有
在四条线段中，如果其中两条线段的比等于另外两条线段比，那么这四条线段叫作成比例线段，简称比例线段.
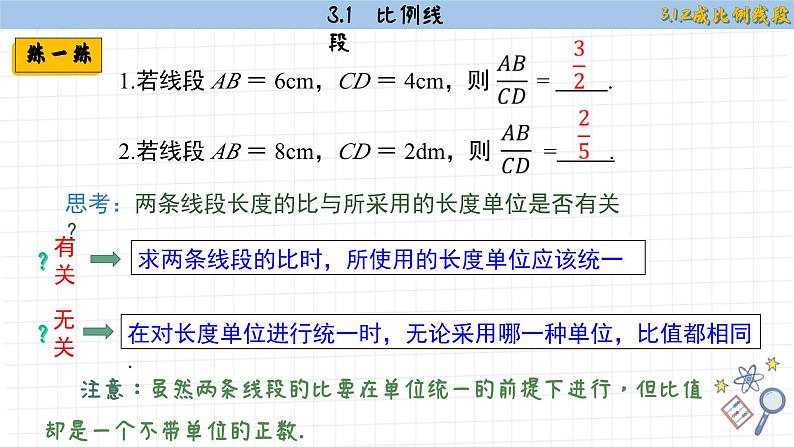
思考：两条线段长度的比与所采用的长度单位是否有关？
求两条线段的比时，所使用的长度单位应该统一
在对长度单位进行统一时，无论采用哪一种单位，比值都相同.
注意：虽然两条线段的比要在单位统一的前提下进行，但比值却是一个不带单位的正数.
那么 a、b、c、d 叫做组成比例的项，
a、d 叫做比例外项，
b、c 叫做比例内项，
d 叫做 a、b、c的第四比例项.
特殊情况：若作为比例内项的两条线段相等，即 a:b=b:c，则b叫做a，c的比例中项.
注意: 1.若 a∶b = k ， 说明a是b的 k 倍； 2.两条线段的比与所采用的长度单位无关，但求比时两条线段的长度单位必须一致； 3.两条线段的比值是一个没有单位的正数； 4.除了a = b外，a∶b ≠ b∶a， 与 互为倒数.
古希腊数学家、天文学家欧多克索斯（Eudxus，约前400—约前347）曾经提出一个问题：
能否将一条线段AB分成不相等的两部分，使较短线段CB与较长线段AC的比等于线段AC与原线段的比？
成立？如果这能做到的话，那么称线段AB被点C黄金分割，点C叫作线段AB的黄金分割点，较长线段AC与原线段AB的比叫作黄金分割.
运用一元二次方程的知识，可以求出黄金分割比的数值.
如图，设线段AB的长度为1个单位，点C为线段AB上一点，且AC的长度为 x 个单位，则CB的长度为 (1-x) 个单位.根据①式，列出方程：
由于 x ≠ 0，因此方程②两边同乘 x，得 1-x = x2，
即 x2 + x - 1 = 0.
思考：点C是线段AB的黄金分割点吗?
视觉生理学的研究成果表明，符合黄金分割的比例形式很容易使人产生视觉上的美感，许多世界著名古建筑物中都包含有“黄金分割比”，例如古希腊的巴台农神庙、印度泰姬陵、巴黎圣母院这些著名建筑的正面高度与底部宽度之比均约为黄金分割比.
巴台农神庙（Parthenm Temple）
想一想：如果把图中用虚线表示的矩形画成如图所示的矩形ABCD，以矩形ABCD 的宽为边在其内部作正方形AEFD，那么我们可以惊奇地发现 ， 点E是AB 的黄金分割点吗？矩形ABCD的宽与长的比是黄金比吗？为什么?
点E是AB的黄金分割点
（即 ）是黄金比
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形.
东方明珠塔，塔高468米.设计师在263米处设计了一个球体，使平直单调的塔身变得丰富多彩，非常协调、美观.
在现代，许多建筑的设计中也采用了黄金分割，例如上海的东方明珠广播电视塔的上球体就处于整个塔身高度的黄金分割处.
在人的面部，五官的分布越符合黄金分割，看起来就越美．
神奇的“黄金分割比”也出现在许多著名艺术作品中，如在意大利著名画家达·芬奇的名作《蒙娜丽莎》中，人物的脸的宽度与高度的比就是一个黄金分割比.
在人体躯干与身高的比例上，肚脐是理想的黄金分割点，即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该穿多高的高跟鞋看起来会更美？
1.已知 a，b，c，d 是比例线段.
（1）若 a = 0.8 cm，b = 1 cm，c = 1 cm，求 d ；
（2）若 a = 12 cm，c = 3 cm，d = 15 cm，求 b ；
（3）若 a = 5 cm，b = 4 cm，d = 8 cm，求 c ；
2.在比例尺 1∶1 000 000 的地图上，量得A，B两地的距离是25cm.求A，B两地之间的实际距离.
解：根据题意可得： A，B两地的实际距离 = 25×1 000 000 = 2.5×107 (cm) = 2.5×105 (m)
3.已知线段AB，点P是它的黄金分割点，AP > BP，设以AP为边的正方形的面积为S1，以PB、AB为边的矩形面积为S2，则S1与S2的关系是（ ） A．S1 > S2 B．S1 < S2 C．S1 = S2 D．S1 ≥ S2
5.小明家搬进了新房，他买了一幅山水画，想挂到书房（书房高3米），请你帮他设计一下，挂在多高能给人赏心悦目的感觉？
4.点C是线段AB的黄金分割点，如果 AB = 4，求线段 AC的长度．
AC = 4×0.618 = 2.472 或者 AC = 4×(1-0.618) = 1.518.
离地面的高度 h = 3×0.618 = 1.854 m
解：根据题意可知， ， AB = 15 ， AC = 10，BD = 6. 则 AD = AB – BD = 15 – 6 = 9. 则
1.一条线段的长度是另一条线段的5倍，则这两条线段的比等于 .
2.已知 a、b、c、d 是成比例线段，其中 a = 3cm，b = 2cm，c = 6cm，则线段 d = .
3.已知三个数2，4，6，添上一个数，使它们能构成一个比例式，则这个数为 .
4.如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.
解: 设AB=1，那么在 Rt△BAE 中，