初中数学湘教版九年级上册3.2 平行线分线段成比例集体备课课件ppt

这是一份初中数学湘教版九年级上册3.2 平行线分线段成比例集体备课课件ppt，共30页。PPT课件主要包含了学习目标，动脑筋，证明猜想特殊，证明猜想一般，想一想，由此得到以下结论，解得AF4，变式训练，∴CD∥AB，∵DN∥CP等内容，欢迎下载使用。
1.了解平行线分线段成比例的基本事实及其推论;（重点）2.会用平行线分线段成比例及其推论解决相关问题.（难点）
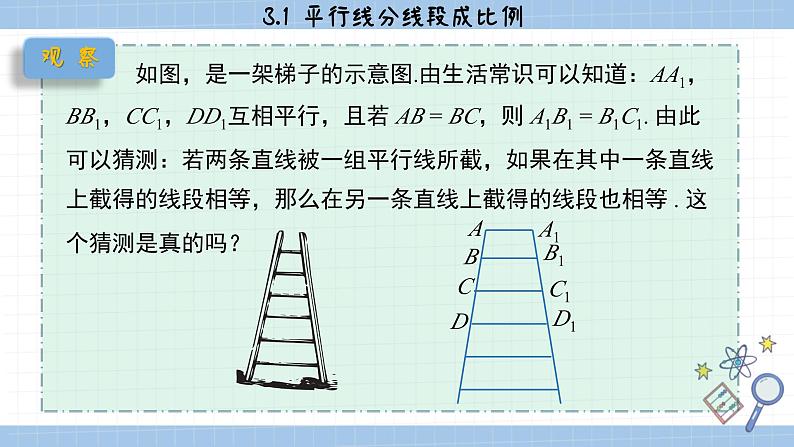
如图，是一架梯子的示意图.由生活常识可以知道：AA1，BB1，CC1，DD1互相平行，且若 AB = BC，则 A1B1 = B1C1. 由此可以猜测：若两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等 . 这个猜测是真的吗？
一、平行线分线段成比例
已知：直线 a∥b∥c，且 AB = BC.求证：A1B1=B1C1
过点 B 作直线 l3//b，分别与直线 a，c相交于点 A2，C2 ，由于 a//b//c，l3//l2，因此由“夹在两平行线间的平行线段相等”可知，
A2B =A1B1，BC2 = B1C1.
如图，已知直线 a//b//c，直线 l1，l2 被直线 a，b，c 截得的线段分别为 AB，BC 和AB1，B1C1，且 AB = BC.
在 △BAA2 和 △BCC2 中，∠ABA2 = ∠CBC2，BA = BC，∠BAA2 = ∠BCC2，因此 △BAA2 ∽ △BCC2.从而 BA2 = BC2,所以 A1B1 = B1C1.
两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等.
二、平行线分线段成比例（基本事实）
把线段 BC 三等分，三等分点为 E，F，分别过点 E，F 作直线 e//a，f//a，分别交 l2 于点 E1，F1.
由于 a // d // b // e // f // c ，
因此 AD = DB = BE = EF = FC .
因此 A1D1 = D1B1 = B1E1 = E1F1 = F1C1.
直线 a // b // c ，直线 l1，l2 被直线 a，b，c 截得的线段分别为 AB，BC 和 A1B1，B1C1，
由此，得到以下基本事实：
我们把以上基本事实简称为平行线分线段成比例 .
1. 如何理解“对应线段”？2.“对应线段”成比例都有哪些表达形式？
如图，已知l1∥l2∥l3，下列比例式中错误的是 ( ) A. B. C. D.
如图，直线 a∥ b∥ c，由平行线分线段成比例的基本事实，我们可以得出图中对应成比例的线段，
把直线 n 向左或向右任意平移，这些线段依然成比例.
三、平行线分线段成比例定理的推论
直线 n 向左平移到 B1 与A1 重合的位置，说说图中有哪些成比例线段？
把图中的部分线擦去，得到新的图形，刚刚所说的线段是否仍然成比例？
直线 n 向左平移到 B2 与A2 重合的位置，说说图中有哪些成比例线段？
把图中的部分线擦去，得到新的图形，刚刚所说的线段是否仍然成比例？
平行于三角形一边的直线截其他两边，所得的对应线段成比例.
如图，在△ABC中， EF∥BC. (1) 如果E、F分别是 AB 和 AC 上的点， AE = BE=7， FC = 4 ，那么 AF 的长是多少？
(2) 如果 AB = 10，AE=6，AF = 5，那么 FC 的长是多 少？
解：由平行线分线段成比例可知，
1、 如图，DE∥BC，AD = 4，DB = 6，AE = 3，则AC = ；FG∥BC，AF = 4.5，则 AG = .
2、如图：在△ABC中，点D、E、F分别在边AB、AC、BC上，且DE//BC、EF//AB.若 AD = 2BD.
解：(1) ∵DE//BC，EF//AB
(2) ∵ AD = 2BD
1.如果，AC，BD相交于点O，直线MN过点O，且BA∥MN∥CD.已知 OA = 3，OB = 1，OD = 2，求OC的长.
解：∵ BA∥MN∥CD，
∵ OA = 3，OB = 1，OD = 2，
∴ OC = 6 .
2.如图，点D，E分别在△ABC的边AB，AC上，且DE∥BC . 若 AB = 3，AD = 2，EC = 1.8，求AC的长 .
解：∵ 在△ABC中 ，DE∥BC，
又∵ CE = 1.8 .
∴ AE = 3.6 ，
∴ AC = AE + CE = 5.4 .
3. 如图，已知菱形 ABCD 内接于△AEF，AE=5cm，AF = 4 cm，求菱形的边长.
解：∵ 四边形 ABCD 为菱形，
设菱形的边长为 x cm，则CD = AD = x cm，DF = (4－x) cm，
4.如图，AB=AC，AD⊥BC于点D，M是AD的中点， CM交AB于点P，DN ∥CP.（1）若AB=6cm，求AP的长；（2）若PM=1cm，求PC的长.
解：(1)∵ AB = AC，AD⊥BC于点D，M是AD的中点, ∴ DB = DC，AM = MD. ∵ DN ∥CP，
又∵AB = 6cm，
∴ AP = 2cm.
（2）若PM = 1cm，求PC的长.
又∵ PM = 1cm，
∴ PC = 2ND = 4PM = 4cm.
解：由（1）知 AP = PN = NB ，