湘教版数学九上第三章复习题（课件PPT）

这是一份湘教版数学九上第三章复习题（课件PPT），共24页。

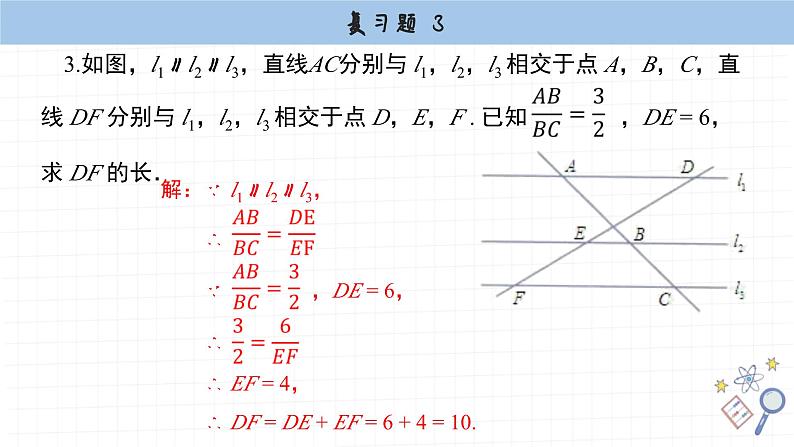
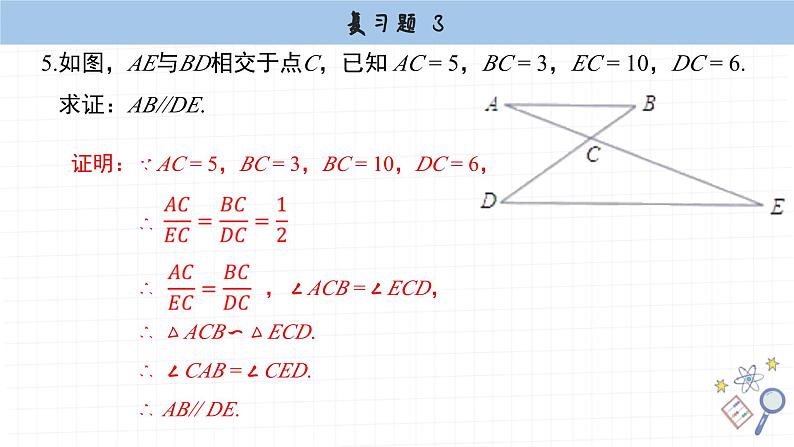
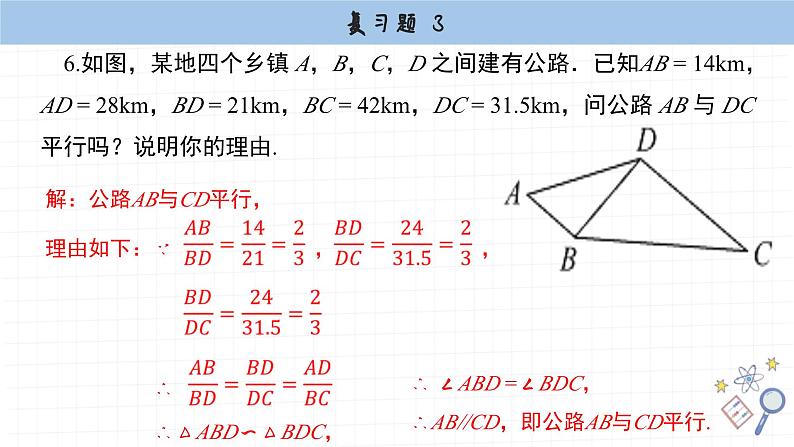
   复习题3第3章 图形的相似1.已知 求下列算式的值： （1） ； （2） .     2.已知 a，b，c，d 是比例线段．（1）若 a = 2，b = 5，c = 6，求 d ；（2）若 a = 1.5，c = 3，d = 4.5，求 b ；（3）若 a = 5，b = 8，d = 44，求 c .解：∵ a，b，c，d 是比例线段，∴ a∶b = c∶d4.根据图中已知条件，试求 D，E 两点之间的距离．CAABDE14.2m28.4m9.8m解：根据图形可得∠ACB =∠ADE = 90°， ∠CAB =∠DAE， ∴ △ACB∽△ADE. ∴ ∴ 解得 ED = 19.6 m. 故 D，E 两点之间的距离为19.6 m.  5.如图，AE与BD相交于点C，已知 AC = 5，BC = 3，EC = 10，DC = 6. 求证：AB//DE. 6.如图，某地四个乡镇 A，B，C，D 之间建有公路．已知AB = 14km，AD = 28km，BD = 21km，BC = 42km，DC = 31.5km，问公路 AB 与 DC平行吗？说明你的理由.∴ ∠ABD =∠BDC，∴AB//CD，即公路AB与CD平行. 7.已知△ABC与△DEF相似且对应中线的比为 2∶3，△ABC的周长和面积分别为 16 和 25 ，求△DEF的周长及面积．解：∵△ABC与△DEF 相似且对应中线的比为2:3， ∴△ABC与△DEF的相似比为2:3. ∴△ABC与△DEF的周长之比为2：3，面积之比为4:9. 又∵△ABC的周长和面积分别为16和25， ∴△DEF的周长及面积分别为24 和 56.25. 8.为了测量一棵树的高度，数学兴趣小组根据光的反射定律(图中∠1=∠2)，把一面镜子放在离树(AB)8m的点 E 处，然后观测者沿着直线 BE后退到点 D，这时恰好在镜子里看到树梢顶点 A，此时量得 DE = 3m.已知观测者目高 CD = 1.5m，求树 AB 的高度．解：∵∠1 =∠2， ∴∠CED =∠AEB. ∵∠CED =∠AEB，∠CDE =∠ABE = 90°， ∴△CED ∽△AEB. ∴解得AB = 4m.故树AB的高度为4m.  9.如图，一教学楼 AB 的高为20m，教学楼后面水塔 CD 的高为30m.已知 BC = 30m，小张的目高 EF 为1.6m.当小张站在教学楼前 E 处时，刚好看到教学楼顶端 A 与水塔顶端 D 在一条直线上，求此时他与教学楼的距离 BE .解：过点F作FN⊥CD，交CD于点N，交AB于点M，如图所示：∵ AM∥DN， ∴△AMF∽△DNF.NM结合已知可得BE=FM，BC=MN=30 m，EF = BM = CN = 1.6 m，FN=FM+MN=BE+BC= (BE+30) m， 10.如图，在平面直角坐标系中，已知五边形OABCD的顶点坐标依次为(0，0)，(4，0)，(5，5)，(2，5)，(0，3).（1）以坐标原点O为位似中心，把各顶点坐标分别放大为原来的1.5倍，所得五边形与原五边形OABCD是位似图形吗？解：把各顶点坐标分别放大为原来的1.5倍， 可得 (0，0)，(6，0)，(7.5，7.5)， (3，7.5)，(0，4.5)， 画出五边形OA′B′C′D′；A′B′C′D′根据位似图形的概念可得五边形OA′B′C′D′和原五边形OABCD是位似图形.（2）以坐标原点O为位似中心，把各顶点坐标分别缩小为原来的，所得五边形与原五边形OABCD是位似图形吗？ 根据位似图形的概念可得五边形OA′′B′′C′′D′′都和原五边形OABCD是位似图形.解：把各顶点坐标分别缩小为原来的， 可得可得 (0，0)，(3.2，0)，(4，4)， (1.6，4)，(0，2.4)， 画出五边形OA′′B′′C′′D′′；A′′B′′C′′D′′ 11.我们可以按以下方法找到线段的黄金分割点： 如图，设 AB 是已知线段，以 AB 为边作正方形 ABCD；取 AD 的中点E，连接 EB；延长 DA 至 F，使 EF = EB；以线段 AF 为边作正方形AFGH，交 AB 于点 H ，则点 H 就是线段 AB 的黄金分割点 . 请试着用上述方法找一条已知线段的黄金分割点 .  已知：线段ab.求作：线段ab的黄金分割点.仿照已知中的方法作出线段ab的黄金分割点，即点h.如图所示：ab12.如图，在RtΔABC中，CD是斜边AB上的高． 求证：（1）AC2 = AD·AB; （2）CD2 = BD·AD. 13.如图，阳光通过窗口AB照射到室内，在地面上留下2.7m宽的亮区 ED.已知光线AE//BD，亮区E点与窗口所在墙脚 C 点之间的距离 EC = 8.7m，窗口高 AB =1.8m，求窗口底边离地面的高 BC .解：∵AE∥BD， ∴△CBD∽△CAE. ∴ 又∵ DC = EC – ED = 8.7 – 2.7 = 6m， AC = BC+AB = BC + 1.8， ∴ 解得 BC = 4m.故窗口底边离地面的高BC为4m.   14.如图，正方形 ABCD 的边长是2，BE = CE，MN = 1，线段 MN 的两端点在 CD，AD 上滑动. 当 DM 为多长时，△ABE 与以 D，M，N 为顶点的三角形相似？请说明理由.      解：四边形A′B′C′D′与四边形ABCD相似. 理由如下：∵ ，∠A′OB′ =∠AOB， ∴△A′OB′∽△AOB. ∴∠OA′B′ = ∠OAB， ∠OB′A′ = ∠OBA. 同理可得 ∠OB′C′ =∠OBC， ∴∠A′B′C′ =∠ABC 同理可得∠B′A′D′ =∠BAD， ∠A′D′C′ = ∠ADC， ∠D′C′B′ = ∠DCB.又∵∴四边形A′B′C′D′∽四边形ABCD.  16.如图，将图中的六边形放大为原图形的2倍，画出所得图形，并写出所得图形的各顶点的坐标 .(1，2)(2，-1)(1，-3)(-1，-2)(-2，0)(-1，2)(-2，4)、(2，4)、(4，-2)、(2，-6)、(-2，-4)、(-4，0) 17.某兴趣学习小组到校外进行数学探究活动，发现一个如图所示的支架PAB，于是他们利用手中已有的工具进行了如下一系列操作： 第一步，测量支架底部A，B两点之间的距离； 第二步，在AP上取一点C，挂上铅垂线CD，使点D恰好落在直线AB上，测量CD和AD的长； 第三步，在BP上取一点E,挂上铅垂线EF，使点F恰好落在直线AB上，测量EF和BF的长 . 已知上述步骤中测得数据如下表： 根据以上数据，你能帮他们计算出支架顶端P到地面的距离吗？如能，请计算出结果(精确到0.1m)；如不能，请说明理由． ∵ CD⊥AB，EF⊥AB，PG⊥AB， ∴ CD // EF // PG. ∴ △ADC ∽△AGP，△BEF∽△BGP. ∴ ， ∴ ， 解得 PG = ≈ 8.3m. 故支架顶端P到地面的距离约为 8.3 m.G     解：过点P作PG垂直地面于点G，如图所示：本课结束