四年级上数学教学反思认识平行_苏教版

认识平行　[教学反思]
　　备课的过程就是解决问题的过程。之所以研究这节课，是想探索几个有关这节课的问题。
　　第一，如何引出直线？
　　苏教版小学数学教材在教学这一内容时，是提供了一些现实生活的场景，然后从中抽象出直线的。我们知道，生活场景中抽象出的其实只是线段。由线段再让学生想象将其无限延长，无疑给学生的思考设置了一层障碍。直接从直线切入本课的教学，更加自然一些，并且学生经历画与观察的过程，尤其是画“与刚才位置关系不同的两条直线”，对“位置关系”会有比较切身的感受。
　　由“画”引出的另一个问题是，学生一开始在白纸上画两条直线，会画出平行线吗？严格意义上的平行线应该是画不出来的。（当然也有学生沿直尺的两条平行边画。）其实，一开始能不能画出严格意义上的平行线并不重要，重要的是学生有没有画平行线的意识，即要让两条直线方向相同，距离相等。只要有这样的意识，就说明他对两条直线的位置关系已经有所思考，这一环节的教学目标也就达到了。
　　第二，如何解读“同一平面”？
　　小学和中学的数学教材中，都是开门见山地提出“同一平面”。就“同一平面”这一知识点来说，教材没有提供任何教学线索。有的教师认为，在没有出现“异面”的情况下，提“同一平面”没有什么必要。这有两种理解：一是不提“同一平面”，二是一开始教学的时候，直接教学“不相交的两条直线互相平行”，然后在出现“异面”的时候补充“同一平面”。第一种情况显然不合适，虽说学生对于平行主要是直观认识，然而用严谨的数学语言描述概念还是必要的。“同一平面”是一个无法回避也不应该回避的问题。第二种情况，感觉上是层层递进，然而总有点儿捉弄人的感觉。一开始，让学生自以为在教师的循循善诱下已经掌握了什么是平行，而且一系列的学习活动都得到了教师的肯定，然后，再被教师告之：你们刚才所学的是不严密的，错误的。
　　我的理解是，首先，从分类的角度说，两条直线按是否在同一个平面内，可分为共面直线和异面直线。在共面直线中，按是否有一个公共点，可分为相交和平行。可见，是否在“同一平面内”是区分相交和平行的前提。既然是前提，那我们就应该在揭示定义时交代清楚。其次，“同一平面”应该是学生默认的一个前提。试想，学生在哪儿见过直线？无非是书上或作业纸上，都是在同一平面内的。太过于平常的东西是最容易被人忽视的，“同一平面”这层纸需要教师来点破。在让学生认识到此前提的充分性的基础上，在后面的长方体中再通过浅显的例子让他们感受到其必要性。
　　第三，如何引导平行线的画法？
　　毋庸置疑，画平行线是本课的一个难点，需要学生联系平行的概念（特点）去思考操作的方法。用直尺和三角板画平行线实际上根据的是“同位角相等，两直线平行”的判定定理。而在小学阶段，“平移”应该是画平行线的“理论基础”（北师大版教材这一内容的课题就叫“平移与平行”），而这一点是可以让学生通过观察加以体会并接受的。之前安排的从平移前后的图形中找互相平行的线段的练习，目的也在于此。
　　然而，真正要使学生理解画平行线的一般方法，还在于尝试中的点拨──怎样才能保证三角尺作平移运动？尝试、改进、总结，再辅以动画演示，学生实实在在地经历了平行线画法的形成过程，对平行线的认识又深入了一层。
　　第四，如何加深对平行线的认识？
　　教材安排了两道画平行线的习题：

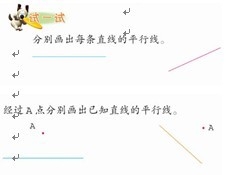
　　从表面上看，这两道题是对学生作图技能要求的提高。然而，如果再深入思考一下，我们可以对这两题进行三个层次的挖掘：第一个层次，技能层面的教学，需要让学生正确地掌握画平行线的方法。第二个层次，画已知直线的平行线和过直线外一点画已知直线的平行线分别能画多少条？在这个层面上，可以让学生对平行公理“过直线外一点，有且只有一条平行线”有一个初步直观的认识。第三个层次，上一题，画出两条平行线，可以引导学生发现另一条平行公理：如果两条直线都和第三条直线平行，这两条直线也互相平行。下一题，引导学生思考：如果过这一点任意画直线，可以画无数条，在这无数条直线当中，却只有一条平行于已知直线，其他无数条直线和已知直线都是相交关系。学生对于“平行”这一特殊的位置关系能有更深刻的体会。
　　这里有两个“无数”和两个“一”，第一个是平行于一条直线的平行线有无数条，然而只有一条经过A点；第二个是经过A点的直线有无数条，然而平行于已知直线的只有一条。相信这两个“无数”和两个“一”可以引导学生对平行线的认识更深入一步。