





精品解析:四川省成都市树德中学高三上学期1月模拟检测理科数学试题
展开树德中学高高三1月模拟检测试题
理科数学
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2. 已知复数![]() 满足
满足![]() (其中
(其中![]() 为虚数单位),则
为虚数单位),则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 荀子曰:“故不积跬步,无以至千里;不积小流,无以成江海.“这句来自先秦时期的名言.此名言中的“积跬步”是“至千里”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 如图,某公园需要修建一段围绕绿地的弯曲绿道(图中虚线)与两条直道(图中实线)平滑连续(相切),已知环绕绿地的弯曲绿道为某三次函数图象的一部分,则该函数的解析式为( )
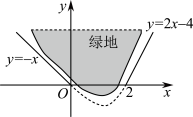
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 足球是由![]() 个正五边形和
个正五边形和![]() 个正六边形组成的.如图,将足球上的一个正六边形和它相邻的正五边形展开放平,若正多边形边长为
个正六边形组成的.如图,将足球上的一个正六边形和它相邻的正五边形展开放平,若正多边形边长为![]() ,
,![]() 、
、![]() 、
、![]() 分别为正多边形的顶点,则
分别为正多边形的顶点,则![]() ( )
( )
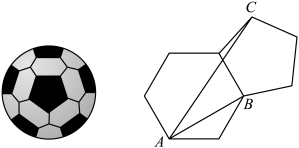
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
6. 已知![]() ,
,![]() ,则
,则![]() 的值等于( )
的值等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 若数列![]() 满足
满足![]() ,
,![]() (
(![]() ,且
,且![]() ),记
),记![]() ,则
,则![]() ( )
( )
A. -1 B. ![]() C.
C. ![]() D.
D. ![]()
8. 某教学软件在刚发布时有100名教师用户,发布5天后有1000名教师用户.如果教师用户人数![]() 与天数
与天数![]() 之间满足关系式:
之间满足关系式:![]() ,其中
,其中![]() 为常数,
为常数,![]() 是刚发布时的教师用户人数,则教师用户超过20000名至少经过的天数为( )(参考数据:
是刚发布时的教师用户人数,则教师用户超过20000名至少经过的天数为( )(参考数据:![]() )
)
A. 9 B. 10 C. 11 D. 12
9. 如图,具有公共![]() 轴的两个直角坐标平面
轴的两个直角坐标平面![]() 和
和![]() 所成的二面角
所成的二面角![]() 轴
轴![]() 等于60°.已知
等于60°.已知![]() 内的曲线
内的曲线![]() 的方程是
的方程是![]() ,则曲线
,则曲线![]() 在
在![]() 内的射影所在曲线方程是( )
内的射影所在曲线方程是( )
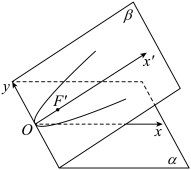
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 已知双曲线![]() :
:![]() 的左右焦点分别是
的左右焦点分别是![]() ,
,![]() ,左右顶点分别是
,左右顶点分别是![]() ,
,![]() ,离心率为2,点P在
,离心率为2,点P在![]() 上,若直线
上,若直线![]() ,
,![]() 的斜率之和为
的斜率之和为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() ( )
( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
11. 在直角![]() 中,角
中,角![]() 为直角,
为直角,![]() ,
,![]() ,点E,F分别在边AB,BC上移动,且
,点E,F分别在边AB,BC上移动,且![]() ,沿
,沿![]() 将
将![]() 折起来得到四棱锥
折起来得到四棱锥![]() ,则该棱锥的体积的最大值是( )
,则该棱锥的体积的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12. 柏拉图多面体并不是由柏拉图所发明,但却是由柏拉图及其追随者对它们所作的研究而得名,由于它们具有高度的对称性及次序感,因而通常被称为正多面体.柏拉图视“四古典元素”中的火元素为正四而体,空气为正八面体,水为正二十面体,土为正六面体.如图,在一个棱长为![]() 的正八面体(正八面体是每个面都是正三角形的八面体)内有一个内切圆柱(圆柱的底面与构成正八面体的两个正四棱锥的底面平行),则这个圆柱的体积的最大值为( )
的正八面体(正八面体是每个面都是正三角形的八面体)内有一个内切圆柱(圆柱的底面与构成正八面体的两个正四棱锥的底面平行),则这个圆柱的体积的最大值为( )
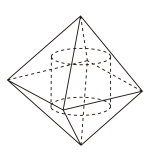
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知实数x,y满足![]() ,
,![]() ,则
,则![]()
取值范围是___________.
14. 如图,某建筑工地搭建的脚手架局部类似于一个![]() 的长方体框架,一个建筑工人欲从 A处沿脚手架攀登至B处,则其最近的行走路线中不连续向上攀登的概率为______________.
的长方体框架,一个建筑工人欲从 A处沿脚手架攀登至B处,则其最近的行走路线中不连续向上攀登的概率为______________.

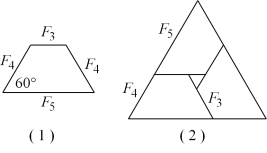
15. 意大利数学家斐波那契于1202年写成《计算之书》,其中第12章提出兔子问题,衍生出数列:1,1,2,3,5,8,13,….记该数列为![]() ,则
,则![]() ,
,![]() ,
,![]() .如图,由三个图(1)中底角为60°等腰梯形可组成一个轮廓为正三角形(图(2))的图形,根据改图所揭示的几何性质,计算
.如图,由三个图(1)中底角为60°等腰梯形可组成一个轮廓为正三角形(图(2))的图形,根据改图所揭示的几何性质,计算![]() ______.
______.
16. 设![]() 表示函数
表示函数![]() 在闭区间
在闭区间![]() 上
上最大值.若正实数
![]() 满足
满足![]() ,则正实数
,则正实数![]() 的取值范围是______.
的取值范围是______.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17. 第22届世界杯于2022年11月21日到12月18日在卡塔尔举办.在决赛中,阿根廷队通过点球战胜法国队获得冠军.

(1)扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有![]() 的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数X的分布列和期望;
的可能性扑不到球.不考虑其它因素,在一次点球大战中,求门将在前三次扑到点球的个数X的分布列和期望;
(2)好成绩的取得离不开平时的努力训练,甲、乙、丙三名前锋队员在某次传接球的训练中,球从甲脚下开始,等可能地随机传向另外2人中的1人,接球者接到球后再等可能地随机传向另外2人中的1人,如此不停地传下去,假设传出的球都能接住.记第n次传球之前球在甲脚下的概率为pn,易知![]() .
.
①试证明:![]()
等比数列;
②设第n次传球之前球在乙脚下的概率为qn,比较p10与q10的大小.
18. 已知各项均不为零的数列![]() 满足
满足![]() ,且
,且![]() ,
,![]() ,设
,设![]() .
.
(1)证明:![]() 为等比数列;
为等比数列;
(2)求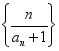
前
![]() 项和
项和![]() .
.
19. 如图,在四棱台![]() 中,底面四边形
中,底面四边形![]() 为菱形,
为菱形,![]() ,
,![]() .
.![]() 平面
平面![]() .
.
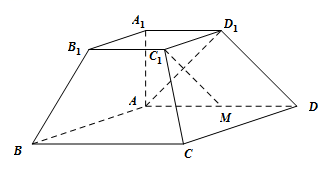
(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求线段
?若存在,求线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
20. 已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上且不在
上且不在![]() 轴上,直线
轴上,直线![]() 与双曲线的交点分别为A,B,直线
与双曲线的交点分别为A,B,直线![]() 与双曲线的交点分别为C,D.
与双曲线的交点分别为C,D.
(1)设直线![]() 和
和![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)问直线l上是否存在点P,使得直线OA,OB,OC,OD的斜率![]() ,
,![]() ,
,![]() ,
,![]() 满足
满足![]() ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
21 已知函数
![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)设![]() 是两个不相等的正数,且
是两个不相等的正数,且![]() ,证明:
,证明:![]() .
.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22. 极坐标系与直角坐标系![]() 有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1`的极坐标方程为
有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1`的极坐标方程为![]() ,曲线C2的参数方程为
,曲线C2的参数方程为![]() (t为参数,)
(t为参数,)![]() ;射线
;射线![]() ,
,![]() ,
,![]() ,
,![]() 与曲线C1分别交异于极点O的四点A,B,C,D
与曲线C1分别交异于极点O的四点A,B,C,D
(1)若曲线![]() 关于曲线
关于曲线![]() 对称,求
对称,求![]() 的值,并把曲线
的值,并把曲线![]() 和
和![]() 化成直角坐标方程;
化成直角坐标方程;
(2)求![]() 的值.
的值.
选修4-5:不等式选讲
23. 选修4—5:不等式选讲
已知函数![]()
(1)若不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() .
.
四川省成都市树德中学2023-2024学年高三上学期开学考试理科数学试题: 这是一份四川省成都市树德中学2023-2024学年高三上学期开学考试理科数学试题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
四川省成都市树德中学2022-2023学年高三上学期1月模拟检测理科数学试题: 这是一份四川省成都市树德中学2022-2023学年高三上学期1月模拟检测理科数学试题,共24页。
精品解析:四川省成都市树德中学高三上学期入学考试数学(理)试题: 这是一份精品解析:四川省成都市树德中学高三上学期入学考试数学(理)试题,文件包含精品解析四川省成都市树德中学高三上学期入学考试数学理试题解析版docx、精品解析四川省成都市树德中学高三上学期入学考试数学理试题原卷版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。












