





精品解析:湖南省长沙市长郡中学、河南省郑州外国语学校 、浙江省杭州第二中学高三二模联考数学试题
展开全国高考数学模拟卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知全集![]() ,集合
,集合![]() ,集合
,集合![]() ,则图中的阴影部分表示的集合为( )
,则图中的阴影部分表示的集合为( )
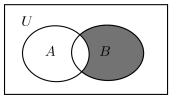
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 已知直线![]() ,若直线
,若直线![]() 与
与![]() 垂直,则
垂直,则![]() 的倾斜角是( )
的倾斜角是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 已知向量![]() ,
,![]() 满足
满足![]() ,则
,则![]() 在
在![]() 方向上的投影向量为( )
方向上的投影向量为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
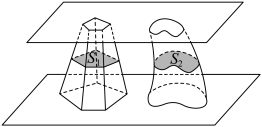
4. 早在公元5世纪,我国数学家祖暅在求球的体积时,就创造性地提出了一个原理:“幂势既同,则积不容异”,即夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积![]() 、
、![]() 总相等,则这两个几何体的体积
总相等,则这两个几何体的体积![]() 、
、![]() 相等.根据“祖暅原理”,“
相等.根据“祖暅原理”,“![]() ”是“
”是“![]() ”的( )
”的( )
A 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 函数![]() 和函数
和函数![]() 的图象相交于
的图象相交于![]() 两点,
两点,![]() 为坐标原点,则
为坐标原点,则![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 已知P为双曲线![]() 上一点,
上一点,![]() 为双曲线C的左、右焦点,若
为双曲线C的左、右焦点,若![]() ,且直线
,且直线![]() 与以C的实轴为直径的圆相切,则C的渐近线方程为( )
与以C的实轴为直径的圆相切,则C的渐近线方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 已知正六棱锥的各顶点都在同一球面上,若该球的体积为![]() ,则该六棱锥体积的最大值为( )
,则该六棱锥体积的最大值为( )
A. ![]() B. 16
B. 16![]() C.
C. ![]() D.
D. ![]()
8. 设实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,则
,则![]() ,
,![]() 的大小关系为( )
的大小关系为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 无法比较
D. 无法比较
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 下列说法正确的是( )
A. 若随机变量![]() ,则
,则![]()
B. 若随机变量![]() ,且
,且![]() ,则
,则![]()
C. 一组数据11,12,12,13,14,15,16,18,20,22的第80百分位数为19
D. 若![]() ,
,![]() ,
,![]() ,则事件
,则事件![]() 与事件
与事件![]() 相互独立
相互独立
10. 在![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 所对的边分别
所对的边分别![]() ,
,![]() ,
,![]() ,
,![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 若![]() ,则
,则![]() B.
B. ![]() 外接圆的半径为
外接圆的半径为![]()
C. ![]() 取得最小值时,
取得最小值时,![]() D.
D. ![]() 时,
时,![]() 取得最大值为
取得最大值为![]()
11. 正四棱柱![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 上的动点(含端点),下列说法正确的是( )
上的动点(含端点),下列说法正确的是( )
A. ![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]()
B. 设![]() 平面
平面![]() ,则
,则![]()
C. 平面![]() 截正四棱柱所得截面周长的最小值为
截正四棱柱所得截面周长的最小值为![]()
D. ![]() 与
与![]() 所成角余弦值的取值范围为
所成角余弦值的取值范围为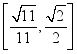
12. 关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 当![]() 时,函数
时,函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
B. 当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减
上单调递减
C. 若函数![]()
![]() 上恰有一个极值,则
上恰有一个极值,则![]()
D 当
![]() 时,
时,![]() ,满足
,满足![]()
三、填空题:本题共4小题,每小题5分,共20分.
13. 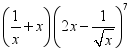 的展开式中常数项为______.
的展开式中常数项为______.
14. 若![]() 是关于
是关于![]() 的实系数一元二次方程的一个根,则该方程可以是______.
的实系数一元二次方程的一个根,则该方程可以是______.
15. 2023年2月22日,中国厦门市一名8岁男孩用时4.305秒单手完成4层汉诺塔游戏,成为新的世界纪录保持者.汉诺塔游戏源于1883年法国数学家卢卡斯提出的汉诺塔问题,有![]() ,
,![]() ,
,![]() 三根柱子,在
三根柱子,在![]() 柱上放着由下向上逐渐变小的
柱上放着由下向上逐渐变小的![]() 个盘子,现要求把
个盘子,现要求把![]() 柱上的盘子全部移到
柱上的盘子全部移到![]() 柱上,且需遵循以下的移动规则:
柱上,且需遵循以下的移动规则:
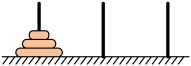
①每次只能移动一个盘子;
②任何时候都不允许大盘子放在小盘子上面;
③移动过程中盘子可以放在![]() ,
,![]() ,
,![]() 中任意一个柱子上.
中任意一个柱子上.
若用![]() 表示
表示![]() 个盘子时最小的移动次数,则
个盘子时最小的移动次数,则![]() ______,
______,![]() ______.
______.
16. 已知抛物线![]() :
:![]() 的准线为
的准线为![]() ,过点
,过点![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的中点为
的中点为![]() ,分别过点
,分别过点![]() ,
,![]() ,
,![]() 作
作![]() 的垂线,垂足依次为
的垂线,垂足依次为![]() ,
,![]() ,
,![]() ,则当
,则当![]() 取最小值时,
取最小值时,![]() ______.
______.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17. 已知函数![]() 的部分图像如图所示,其中
的部分图像如图所示,其中![]() 的图像与
的图像与![]() 轴的一个交点的横坐标为
轴的一个交点的横坐标为![]() .
.
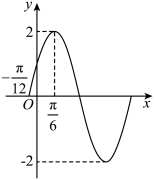
(1)求这个函数的解析式;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围.
的取值范围.
18. 已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() 且
且![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列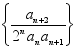 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
19. 如图,正四棱锥![]() 和正三棱锥
和正三棱锥![]() 顶点均为
顶点均为![]() .
.
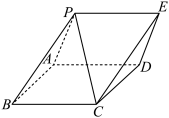
(1)设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,
,![]() 的中点为
的中点为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
20. 某公司有员工140人,为调查员工对薪酬待遇的满意度,现随机抽取了15人,通过问卷调查,有3人对薪酬不满意.
(1)试估计公司中对薪酬不满意的人数;
(2)从15名调查对象中抽取2人,用![]() 表示其中对薪酬不满意的人数,试求
表示其中对薪酬不满意的人数,试求![]() 的数学期望
的数学期望![]() ;
;
(3)实际上,由于问题比较敏感,被调查者为了保护自己的隐私往往会做出相反的回答,导致调查数据失真.为此对调查方法进行优化,现向15名调查对象提供两个问题:
问题A:你对公司薪酬是否不满意?
问题B:现场抛一枚硬币,否正面朝上?
在一个密闭房间里有一个箱子,箱子中放入大小相同的10个小球,其中黑色小球7个,白色小球3个,每位调查对象进入房间后,从箱子中摸出一个小球后放回,若是黑球,则回答问题A,若是白球,则抛硬币完成问题B.若有6人回答“是”,试用全概率公式估计公司中对薪酬不满意的人数.
21. 已知椭圆![]() :
:![]() (
(![]() ),长轴为
),长轴为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 是椭圆
是椭圆![]() 上另两个动点,求
上另两个动点,求![]() 面积的最大值.
面积的最大值.
22. 曲线的曲率是针对曲线上某个点的切线方向角对弧长的转动率,曲线的曲率越大,表示曲线的弯曲程度越大,若记![]() ,则函数
,则函数![]() 在点
在点![]() 处的曲率为
处的曲率为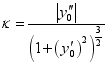 .
.
(1)求证:抛物线![]() (
(![]() )在
)在![]() 处弯曲程度最大;
处弯曲程度最大;
(2)已知函数![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() 曲率为0时
曲率为0时![]() 的最小值分别为
的最小值分别为![]() ,
,![]() ,求证:
,求证:![]() .
.
精品解析:湖南省长沙市长郡中学高三一模数学试题: 这是一份精品解析:湖南省长沙市长郡中学高三一模数学试题,文件包含精品解析湖南省长沙市长郡中学高三一模数学试题解析版docx、精品解析湖南省长沙市长郡中学高三一模数学试题原卷版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
2023届湖南省长沙市长郡中学高三二模数学试题含解析: 这是一份2023届湖南省长沙市长郡中学高三二模数学试题含解析,共21页。试卷主要包含了单选题,多选题,填空题,双空题,解答题等内容,欢迎下载使用。
湖南省长沙市长郡中学2023届高三二模数学试题: 这是一份湖南省长沙市长郡中学2023届高三二模数学试题,文件包含湖南省长沙市长郡中学2023届高三二模数学试题解析版docx、湖南省长沙市长郡中学2023届高三二模数学试题原卷版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。












