初中湘教版3.5 相似三角形的应用习题课件ppt

这是一份初中湘教版3.5 相似三角形的应用习题课件ppt，共8页。

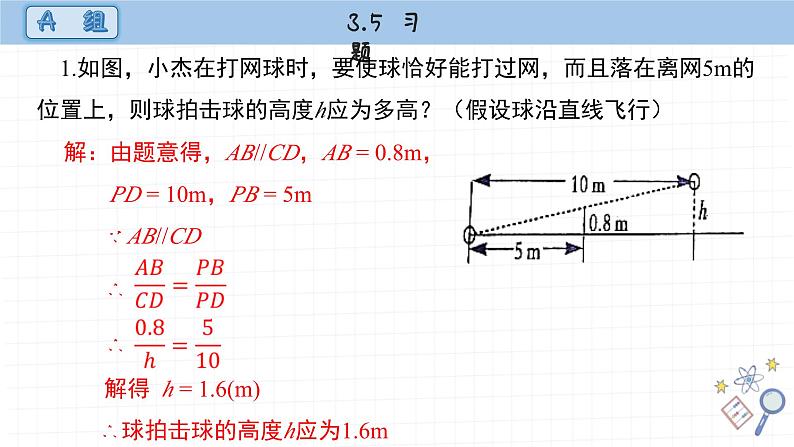
1.如图，小杰在打网球时，要使球恰好能打过网，而且落在离网5m的位置上，则球拍击球的高度h应为多高？（假设球沿直线飞行）
3.如图，某宣传栏BC后面2m处植有与宣传栏平行的6棵树，即DE//BC，且相邻两棵树干之间的间隔均为2m . 一人站在宣传栏前面的点A处正好看到两端的树干，其余的4棵树均被宣传栏挡住．已知AF⊥BC，AF=3m，求宣传栏BC的长（不计宣传栏的厚度）.
解：∵ 6棵树中，相邻两棵树干之间的间隔均为2m， ∴ ED = 2×(6 - 1) = 10 m. 结合已知可得点A到ED的距离为 3 + 2 = 5 m. ∵ DE // BC， ∴△ABC∽△ADE.
4.如图，一张梯子共有5级互相平行的踏板，每相邻两级踏板之间的距离都相等．已知梯子最上面一级踏板的长度A1B1= 0.5m，最下面一级踏板的长度A5B5= 0.8m，求剩余几级踏板的长度（提示：过点A1作B1B5的平行线）．
解：过点A1作B1B5的平行线，使A1D∥ B1B5，
由等分关系：A5D = A5B5- A1B1 = 0.8 - 0.5 = 0.3(m)则每级差为：0.3÷4 = 0.075(m)；A2B2 = 0.5 + 0.075 = 0.575 (m)；A3B3= A2B2 + 0.075 = 0.575 + 0.075 = 0.65(m)A4B4 = A3B3 + 0.075 = 0.65 + 0.075 = 0.725(m)故答案为：A2B2 = 0.575 (m)；A3B3 = 0.65(m)；A4B4 = 0.725(m)
5.在一次活动课上，王老师让同学们到操场上想办法测量旗杆的高度．小芳同学的测量方法是：拿一根高3.5m的竹竿(EC)直立在离旗杆(AB)27m的C处，然后走到D处，这时目测到旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C，D两点间的距离为3m，小芳的目高（眼睛到地面的距离）DF为1.5m，这样便可知道旗杆AB的高度 . 你认为这种测量方法是否可行？如果可行，请求出旗杆的高度；如果不行，请说明理由.
解：这种测量方法可行. 根据梯形DCEF和梯形DBAF相似，即可求出旗杆AB的高度 根据公式 又∵ DC = 3m、 DB = DC + CB = 3 + 27 = 30 m、 竹竿EC = 3.5m 将数据代入上式得： 解得AB = 35m 综上所述，旗杆高35m