2022-2023学年黑龙江省哈尔滨市香坊区风华中学八年级（下）期中数学试卷（五四学制）（含解析）

这是一份2022-2023学年黑龙江省哈尔滨市香坊区风华中学八年级（下）期中数学试卷（五四学制）（含解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年黑龙江省哈尔滨市香坊区风华中学八年级（下）期中数学试卷（五四学制）
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列方程，是一元二次方程的是(    )
A. 2(x−1)=3x B. 1x+x2=0 C. 2x2−x=0 D. x(x−1)=y
2. 由下列线段a，b，c可以组成直角三角形的是(    )
A. a=1，b=2，c=3 B. a=b=1，c= 3
C. a=4，b=5，c=6 D. a=2，b=2 3，c=4
3. 关于x的一元二次方程x2−2x=0根的情况是(    )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 没有实数根 D. 不能确定
4. 平行四边形没有而矩形具有的性质是(    )
A. 对角线相等 B. 对角线互相垂直 C. 对角线互相平分 D. 对角相等
5. 如图，有一个棱长为1m的正方体纸盒，一只昆虫在盒子表面从顶点A爬到顶点B，这只昆虫爬行的最短路线的长是(    )
A. 2m
B. 3m
C. 2m
D. 5m
6. 已知：如图，菱形ABCD中，对角线AC与BD相交于点O，E是BC中点E，AD=6cm，则OE的长为(    )
A. 6cm
B. 4cm
C. 3cm
D. 2cm
7. 下列命题的逆命题成立的是(    )
A. 两直线平行，同旁内角互补
B. 如果a=b，那么a2=b2
C. 若两个数相等，则这两个数的绝对值也相等
D. 对顶角相等
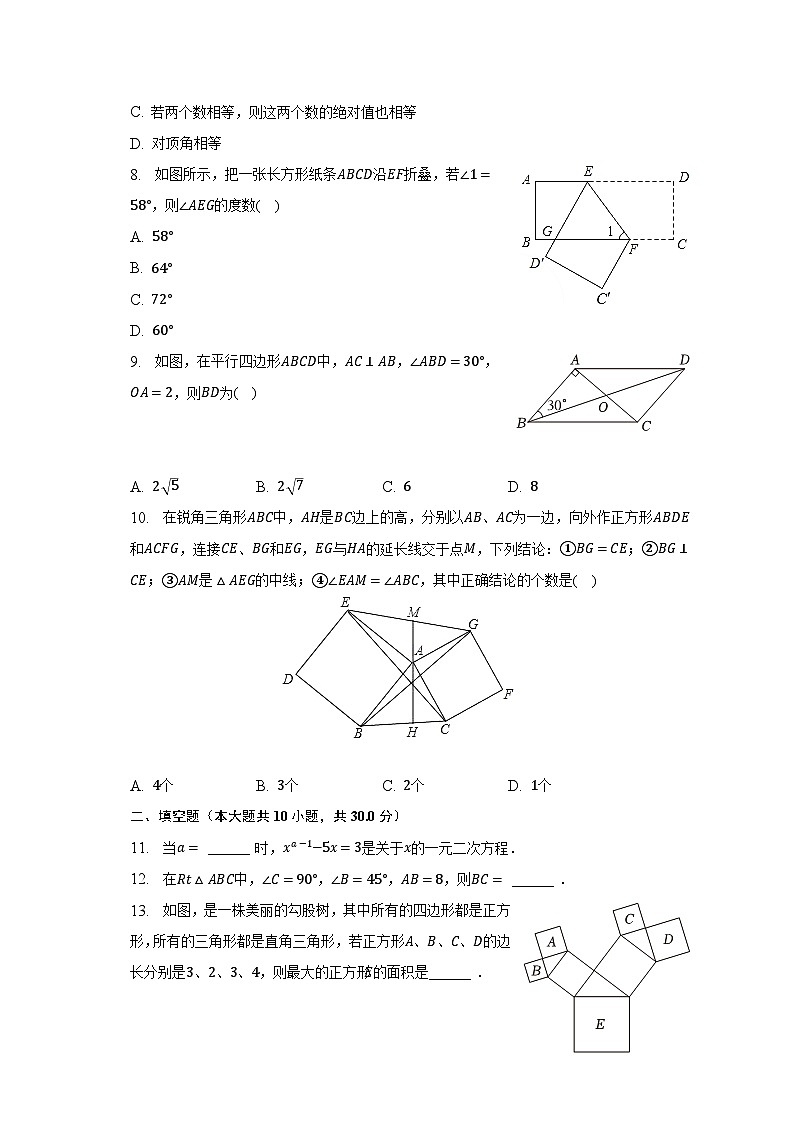
8. 如图所示，把一张长方形纸条ABCD沿EF折叠，若∠1=58°，则∠AEG的度数(    )
A. 58°
B. 64°
C. 72°
D. 60°
9. 如图，在平行四边形ABCD中，AC⊥AB，∠ABD=30°，OA=2，则BD为(    )


A. 2 5 B. 2 7 C. 6 D. 8
10. 在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACFG，连接CE、BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM=∠ABC，其中正确结论的个数是(    )

A. 4个 B. 3个 C. 2个 D. 1个
二、填空题（本大题共10小题，共30.0分）
11. 当a= ______ 时，xa−1−5x=3是关于x的一元二次方程．
12. 在Rt△ABC中，∠C=90°，∠B=45°，AB=8，则BC= ______ ．
13. 如图，是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的边长分别是3、2、3、4，则最大的正方形E的面积是______ ．


14. 已知x=−1是方程x2−ax+1=0的一个根，则a的值为______．
15. 若四边形的两条对角线垂直，则顺次连接该四边形各边中点所得的四边形是______ ．
16. 如图，在菱形ABCD中，AB=5cm，∠BCD=120°，则BD=______cm．


17. 如图，小明从A地沿北偏东30°方向走100m，到B地后再从B地向西走200m到达C地，这时小明离A地______ ．


18. 如图，一根长25m的梯子，斜立在一竖直的墙上，这时梯足距墙底端7m，如果梯子的顶端沿墙下滑4m，那么梯足将滑动______ m.


19. 在平行四边形ABCD中，BC边上的高为4，AB=5，AC=2 5，则平行四边形ABCD周长等于          ．
20. 如图，矩形ABCD中，点F为AD中点，点E在AB边上，∠DCF=2∠BCE，AD=12，AE=4，则线段CE的长度为______ ．


三、解答题（本大题共7小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）
21. (本小题7.0分)
解方程
(1)4(x−3)=2x(x−3)；
(2)x2−4x−7=0．
22. (本小题7.0分)
如图为7×8的正方形网格，每个小正方形的边长为1，请在图中按下列要求画出格点图形(即图形的每个顶点在小正方形的顶点处)．
(1)画出一个以AB为一边的△ABE，点E在小正方形的顶点上，且∠BAE=45°，S△ABE=52．
(2)画出以CD为一边的菱形CDFG，且菱形CDFG的面积为6，连接EG，请直接写出线段EG的长．

23. (本小题8.0分)
如图，在四边形ABCD中∠A=90°，AB=2 3，AD=3，BC=2 7，CD=7.求四边形ABCD的面积．

24. (本小题8.0分)
已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．
(1)求证：AP=BQ；
(2)在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．

25. (本小题10.0分)
“低碳生活，绿色出行”，自行车正逐渐成为人们喜欢的交通工具．某运动商城的自行车销售量自2018年起逐月增加，据统计，该商城2月份销售自行车64辆，4月份销售了100辆．
(1)若该商城2月至4月的自行车销量的月平均增长率相同，问该商城3月份售出多少辆自行车？
(2)考虑到自行车需求不断增加，该商城准备再购进一批两种规格的自行车共100辆，已知A型车的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆．假设所购进车辆全部售完，为使利润不低于26000元，该商城购进A型车不超过多少辆？
26. (本小题10.0分)
如图，矩形ABEF，点D在AF上，将矩形ABEF沿BD折叠，点A的对应点C落在BE上．
(1)如图1，求证：四边形ABCD为正方形．
(2)如图2，四边形ABCD中，点G在AD上，点H在CD上，∠GBH=45°，连接GH，求证：GH=AG+CH．
(3)如图3，在(2)的条件下，连接AC分别交BG、BH于点T、K，连接GK，若AK：KC=2：1，△GKH的面积为20时，求TK的长．


27. (本小题10.0分)
如图，在平面直角坐标系中，直线AB交x轴于点B，交y轴于点A，连接AB，AB= 2OA．
(1)如图1，求∠OBA的度数；
(2)如图2，点D在OB上，BF⊥AB于B，DF⊥AD于D交射线BF于点F，求证：AD=DF．
(3)如图3，在(2)的条件下，点M在x轴正半轴，在AD上取点过点K，作KN//DM交AM于点N，AB=AN，∠BAD=∠AMD，S是AB的中点，R在KD上，∠BAM=2∠ARS，若DF+BD=7 5，求AR的长．


答案和解析

1.【答案】C 
【解析】解：A、方程二次项系数为0，故本选项错误；
B、不是整式方程，故本选项错误；
C、符合一元二次方程的定义，故本选项正确；
D、有两个未知数，故本选项错误．
故选C．
本题根据一元二次方程的定义解答．一元二次方程必须满足四个条件：(1)未知数的最高次数是2；(2)二次项系数不为0；(3)是整式方程；(4)含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．
本题考查了一元二次方程的概念，判断一个方程是否是一元二次方程，首先要看是否是整式方程，然后看化简后是否是只含有一个未知数且未知数的最高次数是2．

2.【答案】D 
【解析】解：A、12+22≠32，故不是直角三角形，故选项错误；
B、12+12=2≠( 3)2，故不是直角三角形，故选项错误；
C、42+52≠62，故不是直角三角形，故选项错误；
D、22+(2 3)2=42，故是直角三角形，故选项正确．
故选：D．
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．

3.【答案】B 
【解析】解：∵△=(−2)2−4×1×0=4>0，
∴方程有两个不相等的实数根．
故选：B．
先计算出△=(−2)2−4×1×0=4>0，然后根据判别式△=b2−4ac的意义即可判断方程根的情况．
本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2−4ac：当△>0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△0，
∴BC= 32=4 2，
故答案为：4 2．
由三角形内角和定理可得∠A=45°，于是Rt△ABC是等腰直角三角形；再利用勾股定理计算求值即可．
本题考查了三角形内角和定理，等腰直角三角形的性质，勾股定理等知识；熟练掌握勾股定理是解题关键．

13.【答案】38 
【解析】解：设中间两个正方形的边长分别为x、y，最大正方形E的边长为z，则由勾股定理得：
x2=32+42=25；
y2=22+32=13；
z2=x2+y2=38；
即最大正方形E的面积为：z2=38．
故答案为：38．
分别设中间两个正方形和最大正方形的边长为x，y，z，由勾股定理得出x2=32+52，y2=22+32，z2=x2+y2，即最大正方形的面积为z2．
本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．

14.【答案】−2 
【解析】解：由题意得：
把x=−1代入方程x2−ax+1=0中，
则(−1)2−a⋅(−1)+1=0，
∴1+a+1=0，
∴a=−2，
故答案为：−2．
直接把x=−1代入方程，即可求出a的值．
本题考查了一元二次方程的解，解题的关键是掌握一元二次方程的解的定义，正确求出a的值．

15.【答案】矩形 
【解析】已知：四边形ABCD中，AC⊥BD，E、F、G、H分别为各边的中点，连接点E、F、G、H．
求证：四边形EFGH是矩形；
证明：∵E、F、G、H分别为各边的中点，
∴EF//AC，GH//AC，EH//BD，FG//BD，(三角形的中位线平行于第三边)
∴四边形EFGH是平行四边形，(两组对边分别平行的四边形是平行四边形)
∵AC⊥BD，EF//AC，EH//BD，
∴∠EMO=∠ENO=90°，
∴四边形EMON是矩形(有三个角是直角的四边形是矩形)，
∴∠MEN=90°，
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形)．
首先根据题意画出图形，写出已知和求证，再根据三角形中位线的性质，可得到这个四边形是平行四边形，再由对角线垂直，能证出有一个角等于90°，则这个四边形为矩形．
本题考查的是矩形的判定方法，常用的方法有三种：①一个角是直角的平行四边形是矩形．②三个角是直角的四边形是矩形．③对角线相等的平行四边形是矩形．

16.【答案】5 3 
【解析】解：如图，

连接AC交BD于点O，
∵四边形ABCD是菱形，
∴AC⊥BD，OB=OD=12BD，BC=AB=5，
∵∠BCD=120°，
∴∠ACB=60°，
∴在Rt△BOC中，
OB=BC×sin60°=5× 32=5 32，
∴BD=2OB=5 3(cm)．
故答案为5 3．
连接AC交BD于点O，根据四边形ABCD是菱形，可得AC⊥BD，OB=OD=12BD，BC=AB=5，再用锐角三角函数求解即可得出结论．
本题考查了菱形的性质、等边三角形的判定与性质，解决本题的关键是掌握菱形的性质．

17.【答案】100 3m 
【解析】解：过点A作AD⊥BC交BC于点D，如图所示：
在Rt△DAB中，
∵∠DAB=30°，AB=100，
∴DB=50，
勾股定理得，DA=50 3，
在Rt△DCA中，
∵BC=200，DB=50，
∴DC=150，
∵DA=50 3，
∴勾股定理得，AC=100 3．
即这时小明离A地100 3m.
故答案为：100 3m.
过点A作AD⊥BC交BC于点D，再根据勾股定理解答即可．
此题主要考查学生对方向角及勾股定理在实际生活中的运用．

18.【答案】8 
【解析】解：梯子顶端距离墙角地距离为 252−72=24m，
顶端下滑后梯子底端距离墙角的距离为 252−(24−4)2=15m，
15−7=8(m)．
故答案为：8．
利用勾股定理进行解答．先求出下滑后梯子底端距离墙角的距离，再计算梯子底端滑动的距离．
此题主要考查了勾股定理的应用，关键是掌握直角三角形两直角边的平方和等于斜边的平方．

19.【答案】20或12 
【解析】解：①如图1所示：
∵在▱ABCD中，BC边上的高为4，AB=5，AC=2 5，
∴EC= AC2−AE2=2，AB=CD=5，
BE= AB2−AE2=3，
∴AD=BC=5，
∴▱ABCD的周长等于20．
②如图2所示：
∵在▱ABCD中，BC边上的高为4，AB=5，AC=2 5，
∴EC= AC2−AE2=2，AB=CD=5，
BE= AB2−AE2=3，
∴BC=3−2=1，
∴▱ABCD的周长等于：1+1+5+5=12，
则▱ABCD的周长等于20或12，
故答案为：20或12．
根据题意分别画出图形，BC边上的高在平行四边形的内部和外部，进而利用勾股定理求出即可．
此题主要考查了平行四边形的性质以及勾股定理等知识，利用分类讨论得出是解题关键．

20.【答案】4 10 
【解析】解：延长CF交BA延长线于M，延长EB到点N，使BE=EN，连接CN，
设∠BCE=α，

∵点F为AD中点，AD=12，
∴DF=FA=6，
在矩形ABCD中，
CD//AB，CD=AB，
∴∠DCF=∠M，
∵∠DFC=∠MFA，
∴△DFC≌△AFM(AAS)，
∴AM=CD，
∵∠DCF=2∠BCE，
∴∠DCF=∠M=2∠α，
∵∠ABC=90°，BE=EN，
∴CE=CN，
∴∠ECB=∠BCN=∠α，
∴∠N=90°−∠α，
∴∠MCN=180°−(2∠α+90°−∠α)
=90°−∠α，
∴∠MCN=∠N，
∴MC=MN，
设BE=x，则MC=MN=4+2x+4+x=3x+8，BM=8+2x，
在Rt△MCB中，根据勾股定理，得CM2=CB2+MB2，
(3x+8)2=144+(8+2x)2，
解得x1=4，x2=−7.2(舍去)，
∴EB=4，
在Rt△ECB中，根据勾股定理，得CE=4 10，
故答案为：4 10．
延长CF交BA延长线于M，延长EB到点N，使BE=EN，连接CN，设∠BCE=α，证明△DFC≌△AFM(AAS)，得出AM=CD，∠DCF=∠M=2∠α，再证明MC=MN，设BE=x，则MC=MN=4+2x+4+x=3x+8，BM=8+2x，在Rt△MCB中，根据勾股定理，得EB=4，在Rt△ECB中，根据勾股定理，得CE长度．
本题主要考查了矩形的性质，熟练应用矩形的性质，辅助线的作法是解题关键．

21.【答案】解：(1)∵4(x−3)=2x(x−3)，
∴4(x−3)−2x(x−3)=0，
则(x−3)(4−2x)=0，
∴x−3=0或4−2x=0，
解得x1=3，x2=2；
(2)∵x2−4x−7=0，
∴x2−4x=7，
则x2−4x+4=7+4，即(x−2)2=11，
∴x−2=± 11，
∴x1=2+ 11，x2=2− 11． 
【解析】(1)先移项，再利用提公因式法将方程的左边因式分解后求解可得；
(2)将常数项移到方程的右边，两边都加上一次项系数一半的平方配成完全平方式后，再开方即可得．
本题主要考查解一元二次方程，解一元二次方程的常用方法有直接开平方法、公式法、因式分解法，解题的关键是根据方程的特点选择合适、简便的方法求解．

22.【答案】解：(1)如图，△ABE即为所求；
(2)如图，四边形CDFG即为所求．EG= 22+32= 13．
 
【解析】(1)作一个等腰直角三角形，使得AE=EB= 5即可；
(2)根据菱形的定义，利用数形结合的思想画出图形．
本题考查作图−应用与设计作图，勾股定理，菱形的性质等知识，解题的关键是学会利用数形结合的思想解决问题．

23.【答案】解：如图，连接BD，
∵∠A=90°，AB=2 3，AD=3，
根据勾股定理，得BD= AB2+AD2= (2 3)2+32=21．
又∵BC=2 7，CD=7，
∵CD2=72=49，BC2+BD2=(2 7)2+( 21)2=28+21=49，
∴CD2=BC2+BD2，
∴∠CBD=90°，
∴S四边形ABCD=S△ABD+S△BCD
=12AB⋅AD+12BD⋅BC
=12×2 3×3+12× 21×2 7
=10 3．
答：四边形ABCD的面积是10 3． 
【解析】连接BD，根据勾股定理求出BD的长，再由勾股定理的逆定理可得△BCD为直角三角形，由S四边形ABCD=S△ABD+S△BCD即可得出结论．
本题考查了勾股定理及勾股定理的逆定理，根据已知条件证得△BCD为直角三角形是解题的难点．

24.【答案】解：(1)∵AQ⊥BE于点Q，
∴∠BQA=90°，
∵DP⊥AQ于点P，
∴∠APD=90°；∠PAD+∠ADP=90°，
在正方形ABCD中，
AD=BA，∠BAD=∠BAQ+∠PAD=90°，
∴∠ADP=∠BAQ，
在△ADP和△BAQ中，
∠APD=∠BQA∠ADP=∠BAQAD=BA
∴△ADP≌△BAQ(AAS)，
∴AP=BQ．
(2)由(1)得△ADP≌△BAQ，
∴AP=BQ，PD=QA，
∴有①AQ−AP=PQ；
②AQ−BQ=PQ；
③DP−AP=PQ；
④DP−BQ=PQ． 
【解析】本题主要考查了正方形以及全等三角形，解决问题的关键是掌握：正方形的四条边相等，四个角都是直角．解题时需要运用：有两角和其中一角的对边对应相等的两个三角形全等，以及全等三角形的对应边相等．
(1)根据正方形的性质得出AD=BA，再根据已知条件得到∠APD=∠BQA，∠ADP=∠BAQ，判定△ADP≌△BAQ(AAS)并得出结论；
(2)根据全等三角形的对应边相等和AQ−AP=PQ进行判断分析．

25.【答案】解：(1)设该商城2月至4月的自行车销量的月平均增长率为x，
根据题意得：64(1+x)2=100，
解得：x1=14=25%，x2=−94(舍去)，
∴64(1+x)=64×(1+25%)=80．
答：该商城3月份售出80辆自行车．
(2)设商城购进A型车m辆，则该商城购进B型车(100−m)辆，
根据题意得：(700−500)m+(1300−1000)(100−m)≥26000，
解得：m≤40．
答：该商城购进A型车不超过40辆． 
【解析】(1)设该商城2月至4月的自行车销量的月平均增长率为x，根据该商城2月及4月自行车的销量，即可得出关于x的一元二次方程，解之即可得出x的值，取其正值，再将其代入3月份的自行车销量=2月份的自行车销量×(1+增长率)中，即可得出结论；
(2)设商城购进A型车m辆，则该商城购进B型车(100−m)辆，根据总利润=每辆自行车的利润×销售数量结合利润不低于26000元，即可得出关于m的一元一次不等式，解之取其最大值即可得出结论．
本题考查了一元二次方程的应用以及一元一次不等式的应用，解题的关键是：(1)找准等量关系，正确列出一元二次方程；(2)根据各数量之间的关系，正确列出一元一次不等式．

26.【答案】(1)证明：如图1，∵四边形ABEF是矩形，
∴∠A=∠ABE=90°，
∵将矩形ABEF沿BD折叠，点A的对应点C落在BE上，
∴∠BCD=∠A=90°，
∴四边形ABCD是矩形，
∵∠ABD=∠CBD，AD⊥BA，CD⊥BC，
∴AD=CD，
∴四边形ABCD是正方形．
(2)证明：如图2，将△ABG绕点B顺时针旋转90°，得到△CBL，则CL=AG，
∵∠BCL=∠A=90°，∠BCH=90°，
∴∠BCL+∠BCH=180°，
∴L、C、H三点在同一条直线上，
∵∠CBL=∠ABG，∠ABC=90°，∠GBH=45°，
∴∠LBH=∠CBL+∠CBH=∠ABG+∠CBH=45°，
∴∠GBH=∠LBH，
∵BG=BL，BH=BH，
∴△GBH≌△LBH(SAS)，
∴GH=LH，
∵LH=CL+CH=AG+CH，
∴GH=AG+CH．
(3)解：如图3，∵AB=CB=AD=CD，∠ABC=∠D=90°，
∴∠BAC=∠BCA=∠DAC=∠DCA=45°，
∴∠GAT=∠KBT=45°，
∵∠ATG=∠BTK，
∴△ATG∽△BTK，
∴ATBT=GTKT，
∴ATGT=BTKT，
∵∠ATB=∠GTK，
∴△ATB∽△GTK，
∴∠KGT=∠BAT=45°，
∴∠BKG=90°，BK=GK，
∵AB//CH，AK：KC=2：1，
∴△ABK∽△CHK，
∴ABCH=BKHK=AKCK=2，
∴BK=2HK，CB=AB=2CH，
∴S△GKB=2S△GKH=2×20=40，
∴12BK⋅GK=12BK2=40，
∴BK=4 5，BG2=BK2+GK2=2BK2=160，
∴HK=12BK=2 5，
∴(2CH)2+CH2=BH2=(4 5+2 5)2，
∴CH=6，
∴CB=AB=2×6=12，
∴AC= CB2+AB2= 122+122=12 2，122+AG2=BG2=160，
∴AG=4，
∵AG//CB，
∴△AGT∽△CBT，
∴ATCT=AGCB=412=13，
∴TK=AC−CK−AT=AC−13AC−14AC=512AC=512×12 2=5 2，
∴TK的长是5 2． 
【解析】(1)由矩形的性质得∠A=∠ABE=90°，由折叠得∠BCD=∠A=90°，则四边形ABCD是矩形，由∠ABD=∠CBD，AD⊥BA，CD⊥BC，根据角平分线的性质得AD=CD，则四边形ABCD是正方形；
(2)将△ABG绕点B顺时针旋转90°，得到△CBL，先证明L、C、H三点在同一条直线上，再证明△GBH≌△LBH，则GH=LH=CL+CH=AG+CH；
(3)先证明△ATG∽△BTK，得ATBT=GTKT，则ATGT=BTKT，再证明△ATB∽△GTK，得∠KGT=∠BAT=45°，则∠BKG=90°，BK=GK，由△ABK∽△CHK，得ABCH=BKHK=AKCK=2，则BK=2HK，CB=AB=2CH，所以S△GKB=2S△GKH=40，则12BK⋅GK=12BK2=40，可求得BK=4 5，BG2=BK2+GK2=2BK2=160，所以HK=12BK=2 5，由勾股定理得(2CH)2+CH2=(4 5+2 5)2，求得CH=6，CB=AB=12，则AC=12 2，122+AG2=BG2=160，所以AG=4，由△AGT∽△CBT，得ATCT=AGCB=13，所以TK=AC−CK−AT=512AC=5 2．
此题重点考查矩形的性质、轴对称的性质、正方形的判定与性质、旋转的性质、等腰直角三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理等知识，此题综合性强，难度较大，属于考试压轴题．

27.【答案】(1)解：∵∠AOB=90°，AB= 2OA，
∴BO= AB2−OA2= ( 2AO)2+(AO)2=AO，
∴∠OBA=∠OAB=12×90°=45°；
(2)证明：过点D作DE⊥OB，交AB于点E，

∵BF⊥AB，DF⊥AD，
∴∠ABF=∠ADF=90°，
∵∠BTF=∠ATD，
∴∠BFD=∠TAD，
由(1)可知∠ABO=45°，
∴∠DBE=∠BED，
∴BD=DE，
又∵∠ADF=∠BDE=90°，
∴∠ADE=∠BDF，
∴△ADE≌△FDB(AAS)，
∴AD=DF；
(3)解：过点A作AC//SR交x轴于点C，交KN于点G，延长AD，过点B作BE//SR，交AD的延长线于点E，延长SR，过点E作EH//AB，交SR的延长线于点H，如图所示：

∵KN//DM，
∴∠ANK=∠AMD，∠AGK=∠ACD，
∵∠BAD=∠AMD，
∴∠BAD=∠ANK，
∴∠AGK=∠CAN+∠ANK=∠CAN+∠BAD，
∵AC//SR，
∴∠ARS=∠DAC，
∵∠BAM=2∠ARS，
∴∠BAM=2∠DAC，
∵∠BAM=∠BAD+∠DAC+∠CAN，
∴∠DAC=∠BAD+∠CAN=∠AGK，
∴∠DAC=∠ACD，
∵AC//SR，BE//SR，
∴BE//SR//AC，
∴∠DEB=∠DAC，∠DBE=∠ACD，
∴∠DEB=∠DBE，
∴DB=DE，
∵AD=DF，
∴AE=AD+DE=DF+DB=7 5，
∵BE//SR，EH//AB，
∴四边形BEHS为平行四边形，
∴EH=SB，
∵S为AB的中点，
∴AS=BS，
∴AS=EH，
∵EH//AB，
∴∠ASR=∠EHR，∠SAR=∠HER，
∴△ASR≌△EHR(ASA)，
∴AR=RE=12AE=7 52． 
【解析】(1)根据勾股定理得BO= AB2−OA2= ( 2AO)2+(AO)2=AO，根据等腰三角形性质得出∠OBA=∠OAB=12×90°=45°；
(2)过点D作DE⊥OB，交AB于点E，证明△ADE≌△FDB(AAS)，由全等三角形的性质得出结论；
(3)过点A作AC//SR交x轴于点C，交KN于点G，延长AD，过点B作BE//SR，交AD的延长线于点E，延长SR，过点E作EH//AB，交SR的延长线于点H，证明∠DEB=∠DBE，得出DB=DE，根据AD=DF，得出AE=DA+DE=DF+DB=7 5，证明四边形BEHS为平行四边形，得出EH=SB，证明△ASR≌△EHR，得出AR=RE=12AE=7 52即可．
本题是三角形综合题，考查了等腰直角三角形的判定与性质，全等三角形的判定与性质，坐标与图形的性质，勾股定理，平行四边形的判定与性质，熟练掌握以上知识是解题的关键．