初中北师大版2.3 绝对值教案配套课件ppt

这是一份初中北师大版2.3 绝对值教案配套课件ppt，共16页。PPT课件主要包含了我怎么就变胖了呢，哈哈我还是我，情境引入，学习目标，什么是相反数，相反数的性质，预习展示，小游戏相反数接龙，观察下图回答问题，探究新知等内容，欢迎下载使用。
有理数王国的公民+1一天不小心掉进了一个魔瓶里。谁知出来后竟变成胖乎乎的0，你说怪不怪？冷眼旁观的2说：“谁叫这瓶里睡着他的相反数兄弟呢？幸好我兄弟不在里面！”
你想知道+1的相反数兄弟是谁吗？为什么他俩见面后就变成0呢？
借助数轴理解相反数和绝对值的概念，会求一个数的相反数和绝对值。
会利用绝对值比较两个负数的大小。
有意识培养我们学习数学的信心和克服困难的勇气，从中体会成功的快乐。
2、互为相反数在数轴上的位置有什么关系呢？
如果两个数只有符号不同，那么我们称其中一个数为另一个数的相反数。特别地，0的相反数是0。
相反数的几何特征：在数轴上，表示互为相反数的两个点，位于原点的两侧，且与原点的距离相等。
（1）正数的相反数是负数。（2 ）0的相反数是0 。（3）负数的相反数是正数。
每组派一名同学作为代表，进行相反数接龙游戏。随便说一个有理数，另一组同学说出它的相反数，循环进行。
任何一个有理数a的相反数是 。
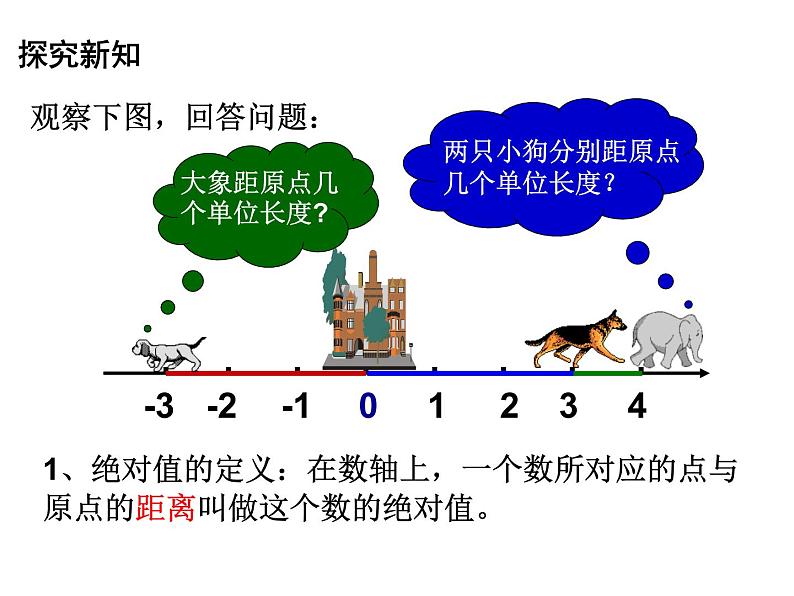
1、绝对值的定义：在数轴上，一个数所对应的点与原点的距离叫做这个数的绝对值。
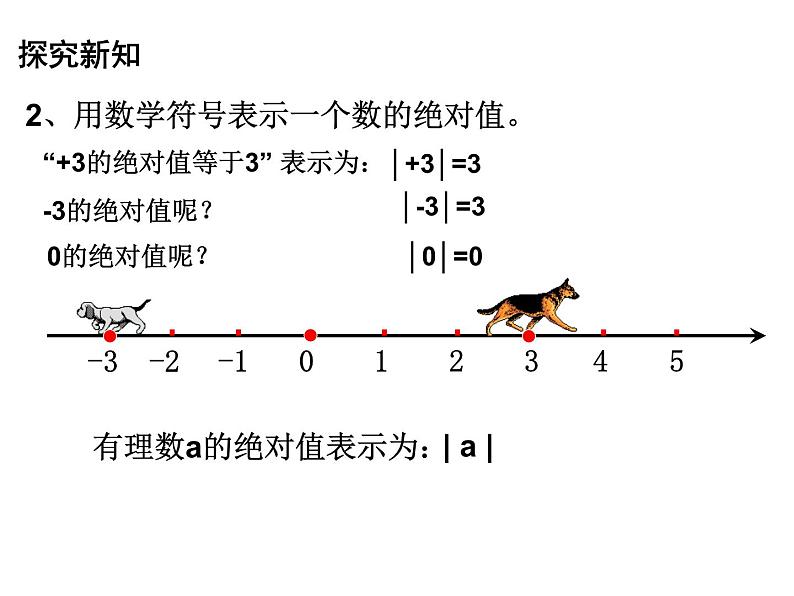
2、用数学符号表示一个数的绝对值。
有理数a的绝对值表示为：
例1、求下列各数的绝对值 ：7.8，-7.8，21，-21， ，- ， 0
解：|7.8| = 7.8；
|-7.8| = 7.8；
| 21| = 21 ；
|-21|= 21 ；
议一议：（1）互为相反数的两个数的绝对值有什么关系?（2）一个数的绝对值与这个数有什么关系?
绝对值的性质：(1)互为相反数的两个数的绝对值相等． (2)正数的绝对值是它本身； 负数的绝对值是它的相反数； 0的绝对值是0.(3)任何一个数的绝对值一定是非负数。
(1)|a|=|-a|；(2)如果a＞0，那么 |a|＝a； 如果a＜0，那么 |a|＝-a； 如果a＝0，那么 |a|＝0。
(1)在数轴上表示下列各数，并比较它们的大小： 　　-1.5，-3，-1，-5； (2)求出(1)中各数的绝对值，并比较它们的大小； (3)你发现了什么?
结论：（1）利用数轴比较两个负数的大小。 （2）两个负数比较大小，绝对值大的反而小。
-5 < -3 < -1.5 < -1
数形结合是学习数学的重要思想
|-5| >|-3 |>|-1.5| > |-1|
2、已知：│x-2│=3，求x的值。
分析：分两种情况讨论 x-2=3 或 x-2=-3 所以， x=5或x=-1
1、已知：│x│=3，求x的值。
3、已知：│x-2│+│y-3│=0，求x+y的值。
解： ∵ │x-2│≥0， │y-3│≥0 且│x-2│+│y-3│=0 ∴|x-2|=0 且| y-3|=0 ∴x=2，y=3 ∴ x+y=2+3=5
1、0的相反数为_____，-2的相反数为_____。
2、 | -8 |=______， | 8 |=_____。3、若| a |=5，则a= _______。
5、- 1 ___ - 5 ，- 0.9 ___ - 0.6；
6、一个数的绝对值是它本身,那么这个数一定是__________。
4、 若|a+1|=0，则a=_______。
我 的 收 获 是 … …
绝 对 值
1、预习作业：《有理数的加法》的预习案完成。2、巩固作业：《课堂精练》的训练案完成。3、提升作业：（各组1号成员完成）（1）（2）