第11讲 圆与圆的位置关系（七大题型）-暑假高一升高二数学衔接知识自学讲义（苏教版）

这是一份第11讲 圆与圆的位置关系（七大题型）-暑假高一升高二数学衔接知识自学讲义（苏教版），文件包含第11讲圆与圆的位置关系七大题型解析版docx、第11讲圆与圆的位置关系七大题型原卷版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
第11讲 圆与圆的位置关系
【题型归纳目录】
题型一：判断圆与圆的位置关系
题型二：求两圆的交点
题型三：由圆的位置关系确定参数
题型四：求两圆的公共弦方程、公共弦长
题型五：圆的公切线条数
题型六：圆的公切线方程
题型七：圆系问题
【知识点梳理】
知识点一：圆与圆的位置关系
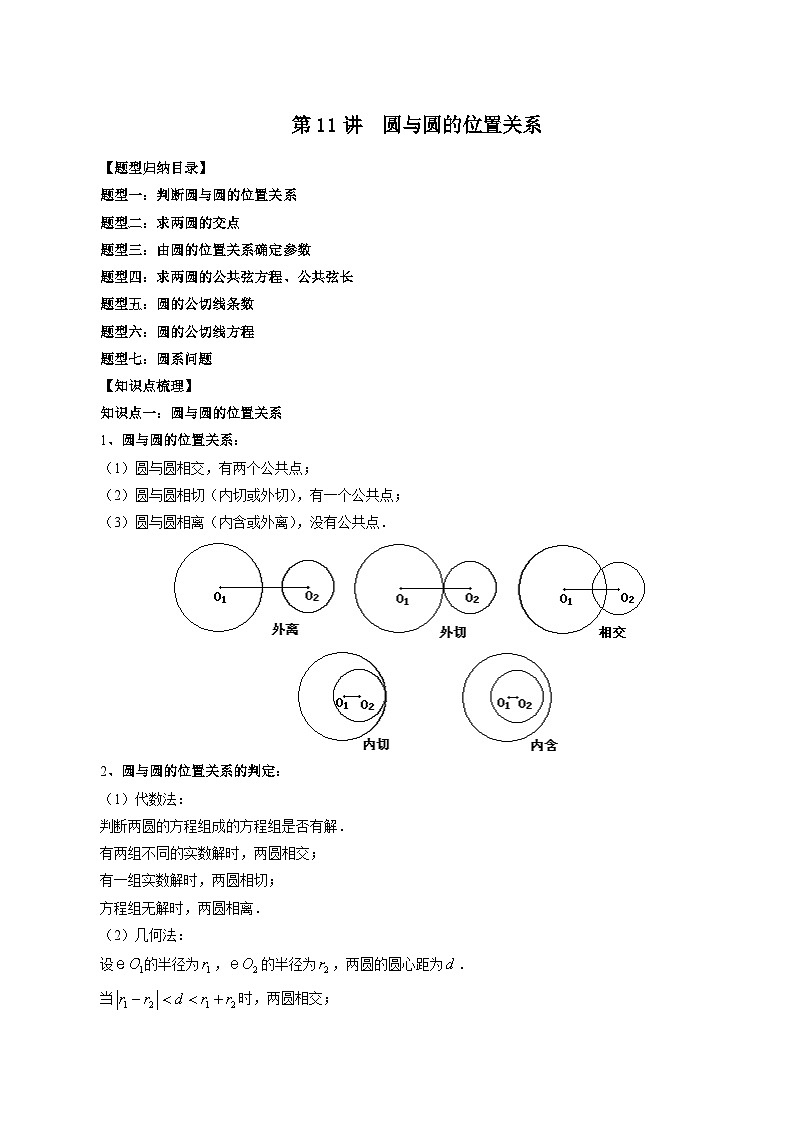
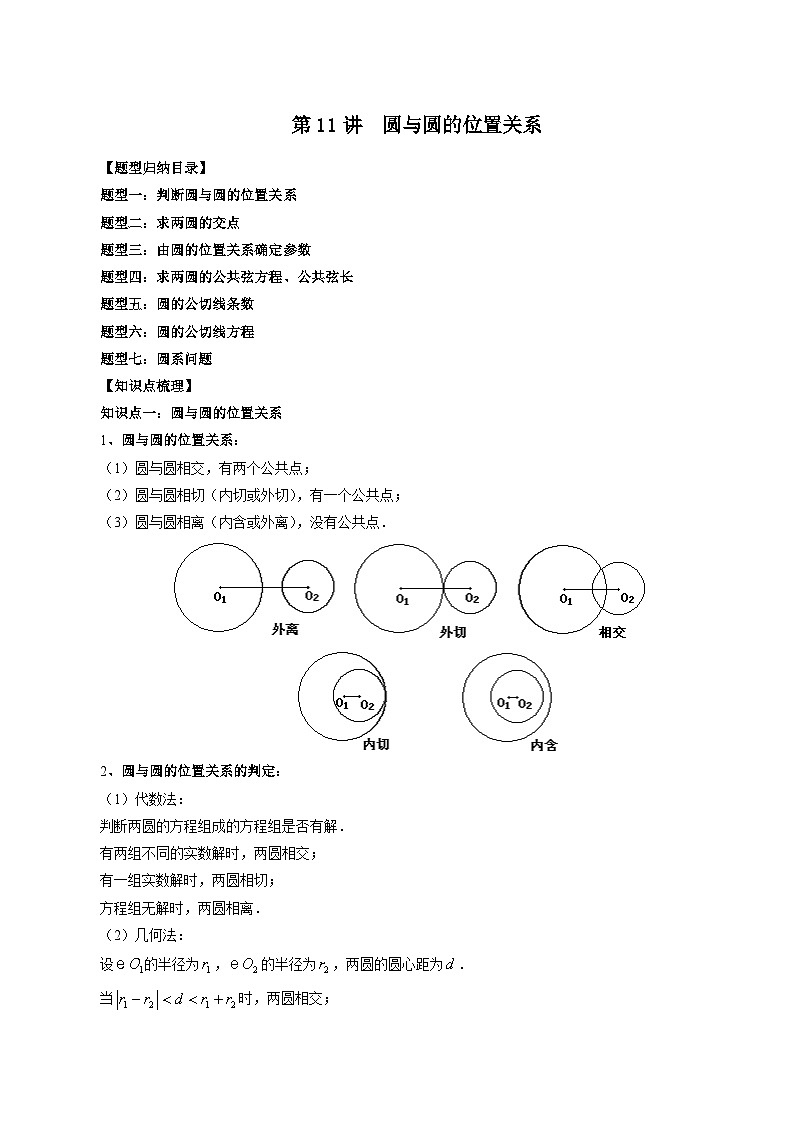
1、圆与圆的位置关系：
（1）圆与圆相交，有两个公共点；
（2）圆与圆相切（内切或外切），有一个公共点；
（3）圆与圆相离（内含或外离），没有公共点．

2、圆与圆的位置关系的判定：
（1）代数法：
判断两圆的方程组成的方程组是否有解．
有两组不同的实数解时，两圆相交；
有一组实数解时，两圆相切；
方程组无解时，两圆相离．
（2）几何法：
设的半径为，的半径为，两圆的圆心距为．
当时，两圆相交；
当时，两圆外切；
当时，两圆外离；
当时，两圆内切；
当时，两圆内含．
知识点诠释：
判定圆与圆的位置关系主要是利用几何法，通过比较两圆的圆心距和两圆的半径的关系来确定，这种方法运算量小．也可利用代数法，但是利用代数法解决时，一是运算量大，二是方程组仅有一解或无解时，两圆的位置关系不明确，还要比较两圆的圆心距和两圆半径的关系来确定．因此，在处理圆与圆的位置关系时，一般不用代数法．
3、两圆公共弦长的求法有两种：
方法一：将两圆的方程联立，解出两交点的坐标，利用两点间的距离公式求其长．
方法二：求出公共弦所在直线的方程，利用勾股定理解直角三角形，求出弦长．
4、两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线，圆的公切线包括外公切线和内公切线两种．
（1）两圆外离时，有2条外公切线和2条内公切线，共4条；
（2）两圆外切时，有2条外公切线和1条内公切线，共3条；
（3）两圆相交时，只有2条外公切线；
（4）两圆内切时，只有1条外公切线；
（5）两圆内含时，无公切线．
【典例例题】
题型一：判断圆与圆的位置关系
【例1】（2023·安徽·高二池州市第一中学校联考阶段练习）圆与圆的位置关系是（    ）
A．外离 B．外切 C．相交 D．内切
【答案】C
【解析】两圆化为标准形式，可得与圆，
可知半径，，于是，
而，故两圆相交，
故选：.
【对点训练1】（2023·山东日照·高二校考阶段练习）两圆和的位置关系是（　　）
A．外离 B．外切 C．相交 D．内切
【答案】B
【解析】由化简得，圆心为，，
由化简得，圆心为，，
两圆心的距离为，
明显地，，所以，两圆的位置关系是外切.
故选：B.
【对点训练2】（2023·天津北辰·高二天津市第四十七中学校考阶段练习）设圆，圆，则圆，的位置（    ）
A．内切 B．相交 C．外切 D．外离
【答案】D
【解析】圆，化为，圆心为，半径为；
圆，化为，圆心为，半径为；
两圆心距离为：，
，
圆与外离，
故选：D.
题型二：求两圆的交点
【例2】（2023·全国·高二专题练习）圆心在直线x﹣y﹣4＝0上，且经过两圆x2+y2﹣4x﹣3＝0，x2+y2﹣4y﹣3＝0的交点的圆的方程为（    ）
A．x2+y2﹣6x+2y﹣3＝0 B．x2+y2+6x+2y﹣3＝0
C．x2+y2﹣6x﹣2y﹣3＝0 D．x2+y2+6x﹣2y﹣3＝0
【答案】A
【解析】由解得两圆交点为与
因为，所以线段的垂直平分线斜率；MN中点P坐标为（1，1）
所以垂直平分线为y＝﹣x+2
由
解得x＝3，y＝﹣1，所以圆心O点坐标为（3，﹣1）
所以r
所以所求圆的方程为（x﹣3）2+（y+1）2＝13即：x2+y2﹣6x+2y﹣3＝0
故选：A
【对点训练3】（2023·重庆永川·高二重庆市永川北山中学校校考期末）平面直角坐标系xOy中，P为圆C1：上的动点，过点P引圆：的切线，切点为T，则满足的点P有（    ）
A．4个 B．3个 C．2个 D．1个
【答案】C
【解析】设点的坐标为，则①，
由已知圆的圆心的坐标为，半径为1，
所以，，
因为，
所以，
化简可得②，
联立①②可得，或，
所以点的坐标为或，
故满足的点P有2个，
故选：C.
题型三：由圆的位置关系确定参数
【例3】（2023·高二课时练习）若圆与圆外切，则＝（    ）
A．21 B．19 C．9 D．
【答案】C
【解析】依题意可得圆与圆的圆心分别为，，则，
又，且两圆外切，则，得到，解得．
故选：C.
【对点训练4】（2023·宁夏吴忠·高二青铜峡市高级中学校考期中）若，，且，则r的取值范围是（    ）
A．(0，] B．(0，1] C．(0，] D．[0，2]
【答案】C
【解析】由知，，
所以圆与圆内切或内含，且圆为大圆，
所以，
所以.
故选：C.
【对点训练5】（2023·贵州黔东南·高二凯里一中校考期末）已知圆与圆有两个交点，则的取值范围是（    ）
A． B．
C． D．
【答案】B
【解析】由题意知，圆心与圆心，
则圆心距，
因为圆与圆有两个交点，
则圆与圆相交，
则，
解得．
故选：B.
题型四：求两圆的公共弦方程、公共弦长
【例4】（2023·福建福州·高二福建省福州高级中学校考期中）圆：与圆：的公共弦长为________.
【答案】
【解析】由题意可知，两圆方程相减可得公共弦方程为，
圆的标准方程为，其圆心，半径；
圆心到公共弦的距离
所以公共弦长为.
故答案为：
【对点训练6】（2023·黑龙江大庆·高二大庆实验中学校考期末）圆与圆的公共弦所在直线方程为___________.
【答案】
【解析】圆的圆心为，半径为，
圆的圆心为，半径为，
则，则两圆相交，
故将两圆方程相减可得：，即，
即圆与圆的公共弦所在直线方程为，
故答案为：
【对点训练7】（2023·湖南长沙·高二长郡中学校考期末）圆与圆的公共弦所在直线的方程为________．
【答案】
【解析】联立两圆的方程得，
两式相减并化简，得，
所以两圆公共弦所在直线的方程为．
故答案为：.
【对点训练8】（2023·全国·高二合肥市第六中学校联考开学考试）圆与圆的公共弦长为______．
【答案】/
【解析】由题意可知，两圆方程相减可得公共弦方程为，
圆的标准方程为，其圆心，半径；
圆心到公共弦的距离
所以公共弦长为.
故答案为：
题型五：圆的公切线条数
【例5】（2023·高二课时练习）已知两圆，，当圆与圆有且仅有两条公切线时，则的取值范围________.
【答案】
【解析】若圆C1与圆C2有且仅有两条公切线时，则两圆相交，
圆心C1，半径R＝2，圆C2，半径r，
则，
若两圆相交，则满足，即,
得，
故答案为：
【对点训练9】（2023·广东·高二统考期末）已知点，，为平面上的动直线，点A，B到直线的距离分别为1，3，则这样的直线有______条．
【答案】4
【解析】到点A的距离为1的直线即该直线与以A为圆心，1为半径的圆相切；
到点B的距离为3的直线即该直线与以B为圆心，3为半径的圆相切；
由于，即两圆相离，如图所示，故公切线的条数为4条，
即点A，B到直线的距离分别为1，3的直线有4条，
故答案为：4.

【对点训练10】（2023·上海普陀·高二上海市晋元高级中学校考期末）平面直角坐标系内，点到直线的距离分别为4和9，则满足条件的直线有__________条.
【答案】3
【解析】由已知可把直线l看成是以为圆心，4为半径的圆的切线，
同时是以为圆心，9为半径的圆的切线，
由于两圆圆心距，所以两圆相外切，
根据外切的两圆的公切线有3条可知，满足条件的直线有3条．
故答案为：3．
【对点训练11】（2023·湖北襄阳·高二襄阳四中校考开学考试）圆与圆的公切线共有__________条
【答案】4
【解析】由，
所以该圆的圆心坐标为，半径为2，
，
所以该圆的圆心坐标为，半径为1，
所以该两圆圆心距为4，两圆半径和为3，
因为，所以两圆的位置关系是外离，
故两圆的公切线共有4条.
故答案为：4.
题型六：圆的公切线方程
【例6】（2023·江西南昌·高二校考阶段练习）如图，圆和圆的圆心分别为、，半径都为，写出一条与圆和圆都相切的直线的方程：_________

【答案】（或或）(答案不唯一)
【解析】如下图所示：

因为圆和圆的圆心分别为、，半径都为，且，
所以，圆和圆外切，易知这两个圆的切点为，且轴，
所以，这两个圆的公切线共条，设这三条切线分别为、、，
其中，切线过点，且轴，则直线的方程为，
设切线分别切圆、圆于点、，连接、，
因为，且，，所以，，
故四边形为矩形，故，
易知直线的方程为，且直线与直线间的距离为，
结合图形可知，直线的方程为，同理可知，直线的方程为.
故答案为： （或或）.(答案不唯一)
【对点训练12】（2023·河南·高二临颍县第一高级中学校联考开学考试）写出与圆和圆都相切的一条直线的方程：__________．
【答案】（答案不唯一）
【解析】由圆，圆，
，可知它们外切，
所以两圆的方程作差即可得内公切线的方程为．
又直线的方程为，两圆半径相等，
故可设外公切线的方程为，
因为圆心到外公切线距离为，
所以或，即两条外公切线的方程分别为和．
故答案为：（答案不唯一）
【对点训练13】（2023·重庆沙坪坝·高二重庆八中校考期末）写出与圆和都相切的一条直线的方程__________．
【答案】///
【解析】因为圆的圆心为，半径
圆的圆心为，半径
又因为
所以圆与圆相离，所以有4条公切线.
画图为：

易得或是圆和的公切线
设另两条公切线方程为：
圆到直线的距离为
圆到直线的距离为
所以
所以或
或
当时
所以，切线方程为
当时
所以
所以
所以或
当时，切线方程为
当时，切线方程为
故答案为：或或或
题型七：圆系问题
【例7】过圆与的交点，且圆心在直线上的圆的方程是_______．
【答案】
【解析】
设圆的方程为，
则，
即，所以圆心坐标为，
把圆心坐标代入，可得，
所以所求圆的方程为．
故答案为：．
【对点训练14】已知圆与圆相交于A、B两点．
（1）求公共弦AB所在直线方程；
（2）求过两圆交点A、B，且过原点的圆的方程．
【解析】（1），①
，②
①-②得
即公共弦AB所在直线方程为．
（2）设圆的方程为
即
因为圆过原点，所以，
所以圆的方程为
【对点训练15】已知圆．求证：对任意不等于的实数，方程是通过两个已知圆交点的圆的方程．
【解析】若是圆、圆的交点坐标，则且，
所以必在上，
又，
所以，则在时，方程表示圆，
综上，对任意不等于的实数，方程是通过两个已知圆交点的圆的方程．
【对点训练16】已知圆和圆．
（1）求证：两圆相交；
（2）求过点，且过两圆交点的圆的方程．
【解析】（1）证明：∵圆，即，表示以为圆心，半径等于2的圆，圆，即，表示以为圆心，半径等于1的圆，所以两圆的圆心距，大于两圆的半径之差且小于两圆的半径之和，故两圆相交．
（2）设过两圆交点的圆的方程为．
把点代入，求得．
故所求圆的方程为，
即．
【过关测试】
一、单选题
1．（2023·高二课时练习）若圆与圆有公共点，则满足的条件是（    ）
A． B．
C． D．
【答案】C
【解析】由得，
两圆圆心之间的距离为＝.
∵两圆有公共点，∴，
∴，
即，∴，
故选：C.
2．（2023·江苏盐城·高二统考期末）在坐标平面内，与点距离为，且与点距离为的直线共有（    ）
A．1条 B．2条 C．3条 D．4条
【答案】A
【解析】当直线的斜率不存在时，直线满足与点距离为，且与点距离为，
以点为圆心，为半径的圆的方程为，
以点为圆心，为半径的圆的方程为，
因为，则两圆相内切，
故两圆的公切线有且仅有条，即，
故在坐标平面内，与点距离为，且与点距离为的直线共有条.
故选：A
3．（2023·福建宁德·高二统考期中）圆与圆的位置关系是（    ）
A．相切 B．相交 C．内含 D．外离
【答案】B
【解析】圆的圆心，半径，
圆的圆心，半径，
于是，
所以两圆相交.
故选：B
4．（2023·浙江嘉兴·高二统考期末）已知圆：与圆：有公共点，则的取值范围为（    ）
A． B． C． D．
【答案】C
【解析】由题知：，，，，
.
因为和有公共点，所以，
解得.
故选：C
5．（2023·浙江丽水·高二统考期末）若圆与圆外切，则实数（    ）
A．－1 B．1 C．1或4 D．4
【答案】D
【解析】由条件化简得，即两圆圆心为，
设其半径分别为，，所以有.
故选：D
6．（2023·河南洛阳·高二统考期末）已知点P为直线上的一点，M，N分别为圆：与圆：上的点，则的最小值为（    ）
A．5 B．3 C．2 D．1
【答案】B
【解析】如图所示，由圆，可得圆心，半径为，
圆，可得圆心，半径为，
可得圆心距，
如图，，
所以，
当共线时，取得最小值，
故的最小值为.

  
故选：B
7．（2023·高二课时练习）若两圆和圆相交，则a的取值范围是（    ）
A． B．或
C． D．或
【答案】B
【解析】圆与圆相交，
两圆的圆心距大于两圆的半径之差的绝对值且小于半径之和，
即，所以.
解得或.
故选：B
8．（2023·广西河池·高二统考期末）已知点是圆上的一点，过点作圆的切线，则切线长的最小值为（    ）
A． B． C． D．
【答案】B
【解析】切线长，所以当取得最小值时，切线长取得最小值.当 共线且点在之间时，
最小，由于,所以min，
所以.
故选：.

  
二、多选题
9．（2023·浙江·高二校联考阶段练习）已知圆的方程为，下列结论正确的是（    ）
A．该圆的面积为 B．点在该圆内
C．该圆与圆相离 D．直线与该圆相切
【答案】BD
【解析】，可知圆心为，半径；
对于A：由圆的半径，得该圆的面积为，故A错误；
对于B：因为，所以点在该圆内，故B正确；
对于C：圆的圆心为，半径为1，
因为两圆心距离为，且，所以两圆相交，故C错误；
对于D：圆心到直线的距离，
所以直线与该圆相切，故D正确，
故选：BD．
10．（2023·甘肃兰州·高二兰大附中校考阶段练习）已知圆和圆，则下列结论正确的是（    ）
A．圆与圆外切
B．直线与圆相切
C．直线被圆所截得的弦长为2
D．若分别为圆和圆上一点，则的最大值为10
【答案】ACD
【解析】圆化为，圆心坐标为，半径为2，
圆化为，圆心坐标为，半径为3.
因为两个圆的圆心距为，等于两个圆半径的和，所以两个圆外切，正确.
圆的圆心到直线的距离为，所以直线与圆不相切，错误.
圆的圆心到直线的距离为，直线被圆所截得的弦长为，C正确.
若分别为圆和圆上一点，则的最大值为，正确.
故选：ACD
11．（2023·广东湛江·高二湛江二十一中校考期中）设，圆与圆的位置关系可能是（    ）
A．内切 B．相交 C．外切 D．外离
【答案】AB
【解析】由题意已知两圆圆心距为，半径分别为，
，因此，也可能,∴两圆相交或内切或内含，
故选：AB．
12．（2023·福建福州·高二校联考期末）已知圆，则下列说法正确的是（    ）
A．圆C的半径为18
B．圆C截x轴所得的弦长为
C．圆C与圆相外切
D．若圆C上有且仅有两点到直线的距离为1，则实数m的取值范围是
【答案】BC
【解析】A：将一般式配方可得：，A错；
B：圆心到x轴的距离为2，弦长为，B对；
C：由题意，，所以圆C与圆外切，C对；
D： 圆C上有且仅有两点到直线的距离为1，d表示圆心与直线的距离，
，则，解之: ，D错；
故选：BC.
三、填空题
13．（2023·全国·高二卫辉一中校联考阶段练习）已知圆：过圆：的圆心，则两圆相交弦的方程为______.
【答案】
【解析】圆：的圆心坐标为，
因为圆过圆的圆心，所以，
所以，所以：，
两圆的方程相减可得相交弦方程为.
故答案为：.
14．（2023·高二课时练习）到点、的距离分别为和的直线有________条．
【答案】
【解析】到点的距离为3的直线是以为圆心，为半径的圆的切线；
同理，到点的距离为的直线是以为圆心，半径为的圆的切线，
所以满足题设条件的直线是这两圆的公切线，
而这两圆的圆心距，则，
所以圆和圆外离，因此它们的公切线有条，即满足条件的直线有条.
故答案为：.
15．（2023·四川资阳·高二四川省资阳中学校考期中）已知圆与圆恰有两条公切线，则实数的取值范围________．
【答案】
【解析】由，即，
可知圆的圆心为，半径为；
因为圆与圆恰有两条公切线，所以圆与圆相交，
则，∵，
解得：，即的取值范围是.
故答案为：.
16．（2023·高二单元测试）已知圆和圆的公共弦所在直线恒过定点M，且点M在直线 上，则的最小值为_____.
【答案】
【解析】由圆和圆，
两式相减，可得公共弦的方程为，即，
联立方程组，解得，即公共弦恒过点，
又由点在直线上，可得在 上，
因为可以看出点到原点的距离，
又因为原点到直线的距离为，
即的最小值为.
故答案为：.
四、解答题
17．（2023·广东深圳·高二深圳中学校考期中）已知圆C的圆心为，且与直线相切．
(1)求圆C的方程；
(2)求圆C与圆的公共弦的长．
【解析】（1）由题意得圆C的半径为，
故圆C的方程为；
（2）圆和的圆心距为，
而，即两圆相交，
将和相减得，
圆的圆心到的距离为，
故两圆的公共弦长为.
18．（2023·黑龙江大庆·高二大庆实验中学校考期末）过点可以作两条直线与圆相切，切点分别为
(1)求实数的取值范围.
(2)当时，存在直线吗？若存在求出直线方程，若不存在说明理由.
【解析】（1）由题意可知，点在圆外，即，解得.
又因为圆，即，
所以，即或，
综上，实数的取值范围是.
（2）当时，，
即，所以圆心，
因为与圆相切，所以四点共圆且以为直径.
设过四点的圆上一点，
则，即，即
所以过过四点的圆的方程为，
两圆方程相减得，
于是直线的方程为.
19．（2023·四川成都·高二校考阶段练习）如图，圆，点为直线上一动点，动点P引圆M的两条切线，切点分别为A、B．

(1)若，求两条切线所在的直线方程；
(2)求线段AB的最小值；
(3)求直线AB的方程，并写出直线AB所经过的定点的坐标．
【解析】（1）设圆M的过点P的切线方程为，即.
数到直线的距离 解得 或
则切线方程为和.
（2）（2）连接PM，AB交于点N，
设，则，

在中， ，
由，则，有 ，
所以.
（3），， ，
故以P为圆心，以为半径的圆P的方程为，
两圆相减，可得为圆P和圆M的公共弦AB所在直线方程，
即，所以直线AB过定点
20．（2023·福建莆田·高二莆田一中校考期末）（1）已知圆与圆.证明圆与圆相交；并求两圆公共弦所在直线的方程；
（2）求圆心既在第一象限又在直线上，与x轴相切，且被直线截得的弦长为的圆的方程.
【解析】（1）证明：圆的圆心为，半径为，
圆化为标准方程，
所以圆心为，半径为，
所以，
因为，
所以圆与圆相交.
由圆与圆，
将两圆方程相减，可得，即，
所以两圆公共弦所在直线的方程为.
（2）设所求圆圆心为，，，半径为，
则圆心到直线的距离为，
由题意，可得，解得，，，
故所求圆的方程为.
21．（2023·山东东营·高二统考期末）已知圆C与圆M：相外切，且圆心C与点关于直线l：对称．
(1)求圆C的标准方程；
(2)求经过点圆C的切线的方程．
【解析】（1）因为，故点在直线上，
故点关于直线的对称点是其本身，
故圆心坐标为，
因为圆C与圆M：相外切，设圆C的半径为，
所以，解得：，
故圆C的标准方程为；
（2）当切线斜率不存在时，即，
此时圆心到的距离为3，等于半径，故满足相切关系，
当切线斜率存在时，设为，
则圆心到直线的距离，
解得：，
故切线方程为，即，
所以切线方程为或.
22．（2023·湖南衡阳·高二衡阳市一中校考阶段练习）已知两个定，，动点满足.设动点的轨迹为曲线，直线：.
(1)求曲线的轨迹方程；
(2)若与曲线交于不同的C，D两点，且（O为坐标原点），求直线的斜率；
(3)若，Q是直线上的动点，过Q作曲线E的两条切线QM，ON，切点为M，N，探究：直线MN是否过定点，若有，请求出该定点，否则说明理由.
【解析】（1）设，由，
得，
整理即.
（2）易知为等腰直角三角形，
点到直线的距离为，
即，故.
（3）设，则，
，
故以为圆心，为半径的圆的方程
为，
将的方程与曲线的方程相减，得
，
即对恒成立，
由，得，
故直线过定点.