第02讲 集合的表示-新高一数学暑假精品课（苏教版必修第一册）

这是一份第02讲 集合的表示-新高一数学暑假精品课（苏教版必修第一册），文件包含第02讲集合的表示解析版docx、第02讲集合的表示原卷版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
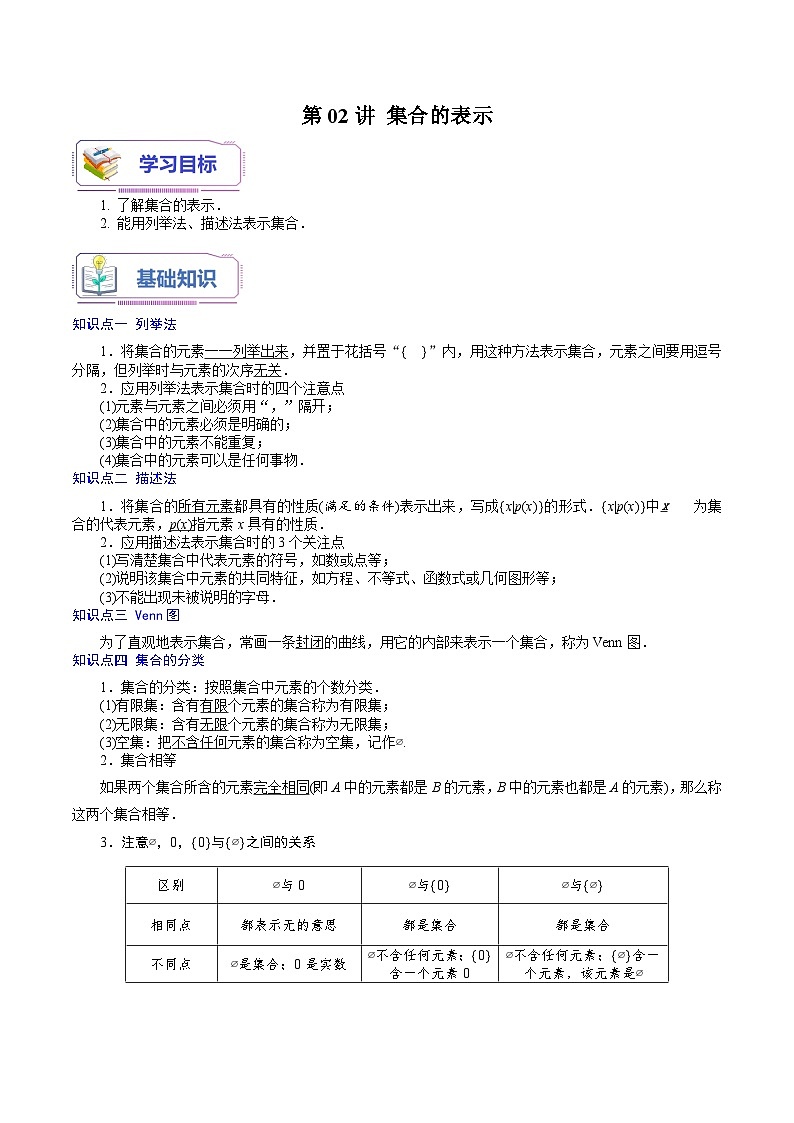
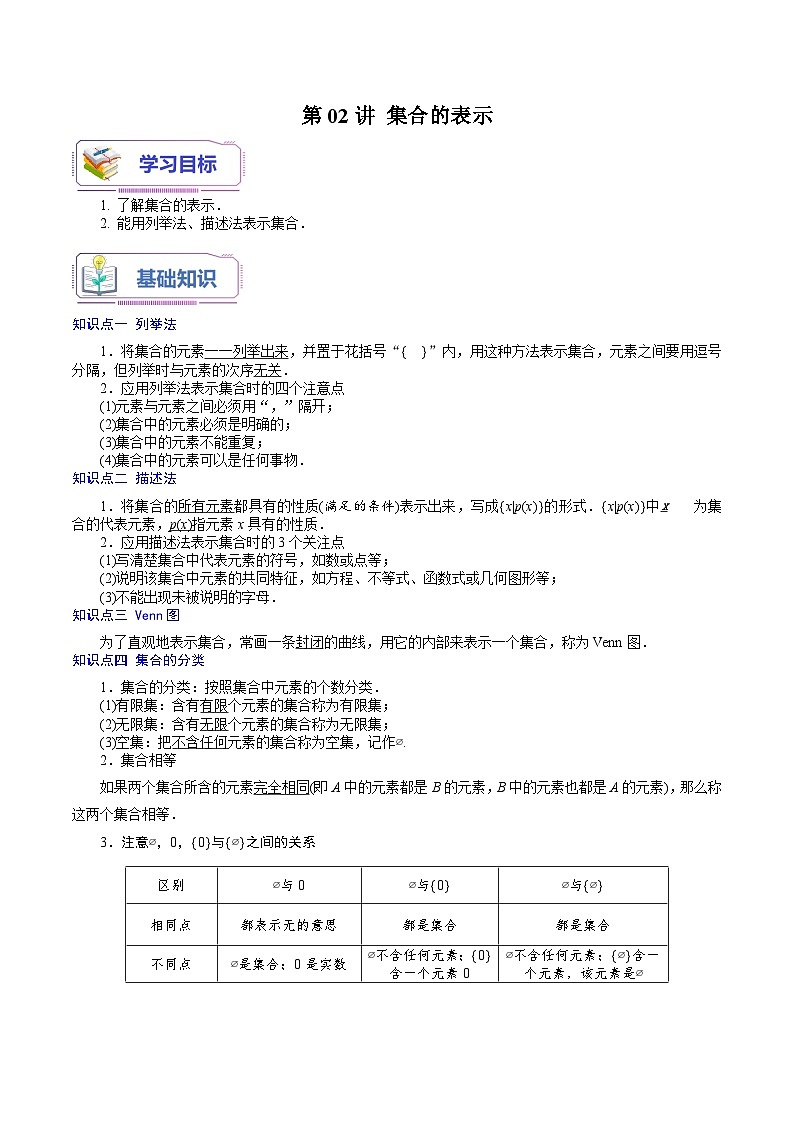
第02讲 集合的表示

1. 了解集合的表示．
2. 能用列举法、描述法表示集合．

知识点一 列举法
1．将集合的元素一一列举出来，并置于花括号“{　}”内，用这种方法表示集合，元素之间要用逗号分隔，但列举时与元素的次序无关．
2．应用列举法表示集合时的四个注意点
(1)元素与元素之间必须用“，”隔开；
(2)集合中的元素必须是明确的；
(3)集合中的元素不能重复；
(4)集合中的元素可以是任何事物．
知识点二 描述法
1．将集合的所有元素都具有的性质(满足的条件)表示出来，写成{x|p(x)}的形式．{x|p(x)}中为集合的代表元素，p(x)指元素x具有的性质．
2．应用描述法表示集合时的3个关注点
(1)写清楚集合中代表元素的符号，如数或点等；
(2)说明该集合中元素的共同特征，如方程、不等式、函数式或几何图形等；
(3)不能出现未被说明的字母．
知识点三 Venn图
为了直观地表示集合，常画一条封闭的曲线，用它的内部来表示一个集合，称为Venn图．
知识点四 集合的分类
1．集合的分类：按照集合中元素的个数分类．
(1)有限集：含有有限个元素的集合称为有限集；
(2)无限集：含有无限个元素的集合称为无限集；
(3)空集：把不含任何元素的集合称为空集，记作∅.
2．集合相等
如果两个集合所含的元素完全相同(即A中的元素都是B的元素，B中的元素也都是A的元素)，那么称这两个集合相等．
3．注意∅，0，{0}与{∅}之间的关系

区别
∅与0
∅与{0}
∅与{∅}
相同点
都表示无的意思
都是集合
都是集合
不同点
∅是集合；0是实数
∅不含任何元素；{0}含一个元素0
∅不含任何元素；{∅}含一个元素，该元素是∅


考点一：用列举法表示集合
例1 用列举法表示下列集合．
(1)不大于10的非负偶数组成的集合；
(2)方程x3＝x的所有实数解组成的集合；
(3)一次函数y＝2x＋1的图象与y轴的交点所组成的集合．
【解析】(1)因为不大于10是指小于或等于10，非负是大于或等于0的意思，所以不大于10的非负偶数集是{0，2，4，6，8，10}．
(2)方程x3＝x的解是x＝0或x＝1或x＝－1，所以方程的解组成的集合为{0，1，－1}．
(3)将x＝0代入y＝2x＋1，得y＝1，即交点是(0，1)，故交点组成的集合是{(0，1)}．
【总结】
用列举法表示集合的3个步骤
(1)求出集合的元素；
(2)把元素一一列举出来，且相同元素只能列举一次；
(3)用花括号括起来．
变式 用列举法表示下列给定的集合．
(1)大于1且小于6的整数组成的集合A；
(2)方程x2－9＝0的实数根组成的集合B；
(3)一次函数y＝x＋3与y＝－2x＋6的图象的交点组成的集合C.
【解析】(1)因为大于1且小于6的整数包括2，3，4，5，
所以A＝{2，3，4，5}．
(2)因为方程x2－9＝0的实数根为－3，3，
所以B＝{－3，3}．
(3)由得
所以一次函数y＝x＋3与y＝－2x＋6的交点为(1，4)，所以C＝{(1，4)}．

考点二：用描述法表示集合
例2 用描述法表示下列集合．
(1)被3除余1的正整数的集合；
(2)坐标平面内第一象限的点的集合；
(3)大于4的所有偶数．
【解析】(1)根据被除数＝商×除数＋余数，可知此集合表示为{x|x＝3n＋1，n∈N}．
(2)第一象限内的点的横、纵坐标均大于零，故此集合可表示为{(x，y)|x>0，y>0}．
(3)偶数可表示为2n，n∈Z，又因为大于4，故n≥3，从而用描述法表示此集合为{x|x＝2n，n∈Z且n≥3}．
【总结】
用描述法表示集合的2个步骤

[注意]　描述法的特点是形式简单、应用方便，通常用于表示元素具有明显共同特征的集合，当元素共同特征不易寻找或元素的限制条件较多时，就不宜采用描述法．
变式 用描述法表示下列集合：
(1)函数y＝－2x2＋x图象上的所有点组成的集合；
(2)不等式2x－3