第10讲 从函数观点看一元二次方程和一元二次不等式-新高一数学暑假精品课（苏教版必修第一册）

这是一份第10讲 从函数观点看一元二次方程和一元二次不等式-新高一数学暑假精品课（苏教版必修第一册），文件包含第10讲从函数观点看一元二次方程和一元二次不等式解析版docx、第10讲从函数观点看一元二次方程和一元二次不等式原卷版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

第10讲 从函数观点看一元二次方程和一元二次不等式

1．会结合一元二次函数的图象，判断一元二次方程实根的存在性及实根的个数．
2．了解函数的零点与方程根的关系．
3．经历从实际情境中抽象出一元二次不等式的过程，了解一元二次不等式的现实意义．能借助一元二次函数求解一元二次不等式，并能用集合表示一元二次不等式的解集．　
4．借助一元二次函数的图象，了解一元二次不等式与相应函数、方程的联系．

知识点一 二次函数的零点
1．一般地，一元二次方程ax2＋bx＋c＝0(a≠0)的根就是二次函数y＝ax2＋bx＋c(a≠0)当函数值取时自变量x的值，即二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴交点的横坐标，也称为二次函数y＝ax2＋bx＋c(a≠0)的零点．
2．函数的零点不是点，而是一个实数，是函数的图象与x轴交点的横坐标，也是函数值为零时自变量x的值，也是函数相应的方程的实数根．
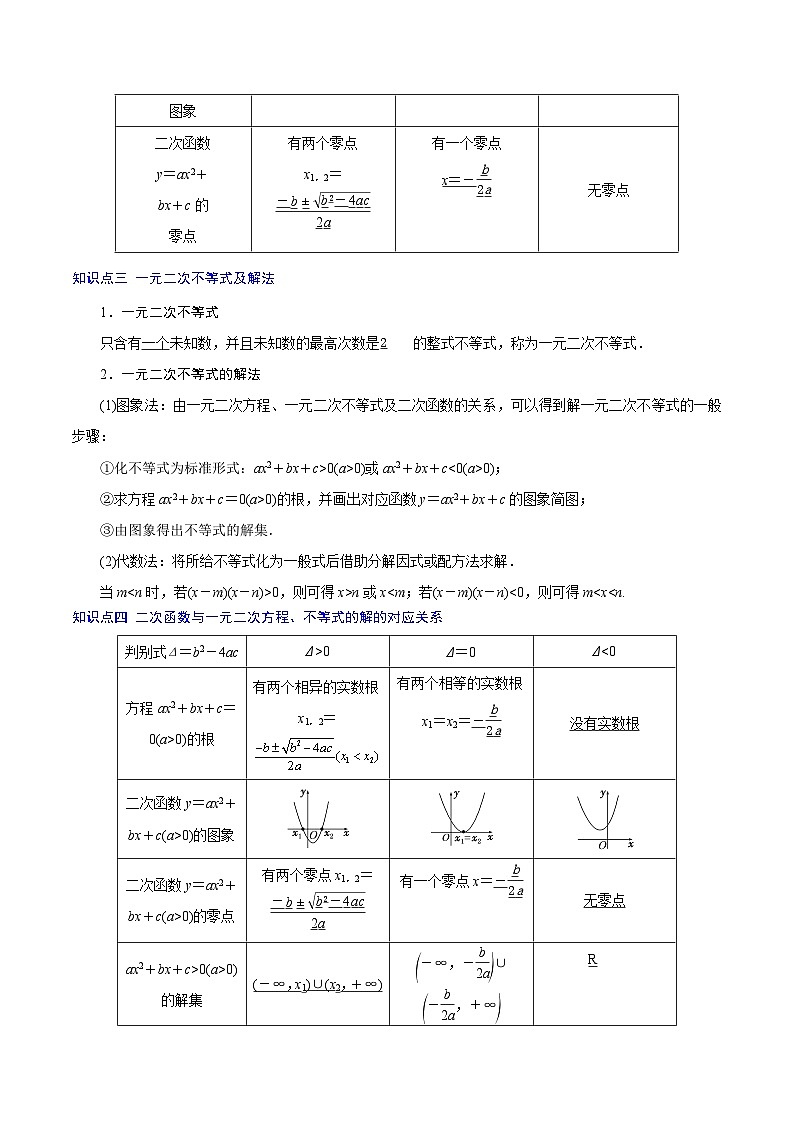
知识点二 一元二次方程的根、二次函数的图象、二次函数的零点之间的关系
当a>0时，一元二次方程ax2＋bx＋c＝0的根、二次函数y＝ax2＋bx＋c的图象、二次函数y＝ax2＋bx＋c的零点之间的关系如表所示：
判别式
Δ＝b2－4ac
Δ>0
Δ＝0
Δ<0
方程ax2＋
bx＋c＝0
的根
有两个相异
的实数根
x1，2＝

有两个相等
的实数根
x1＝x2＝
－
没有实数根
二次函数
y＝ax2＋
bx＋c的
图象



二次函数
y＝ax2＋
bx＋c的
零点
有两个零点
x1，2＝

有一个零点
x＝－
无零点

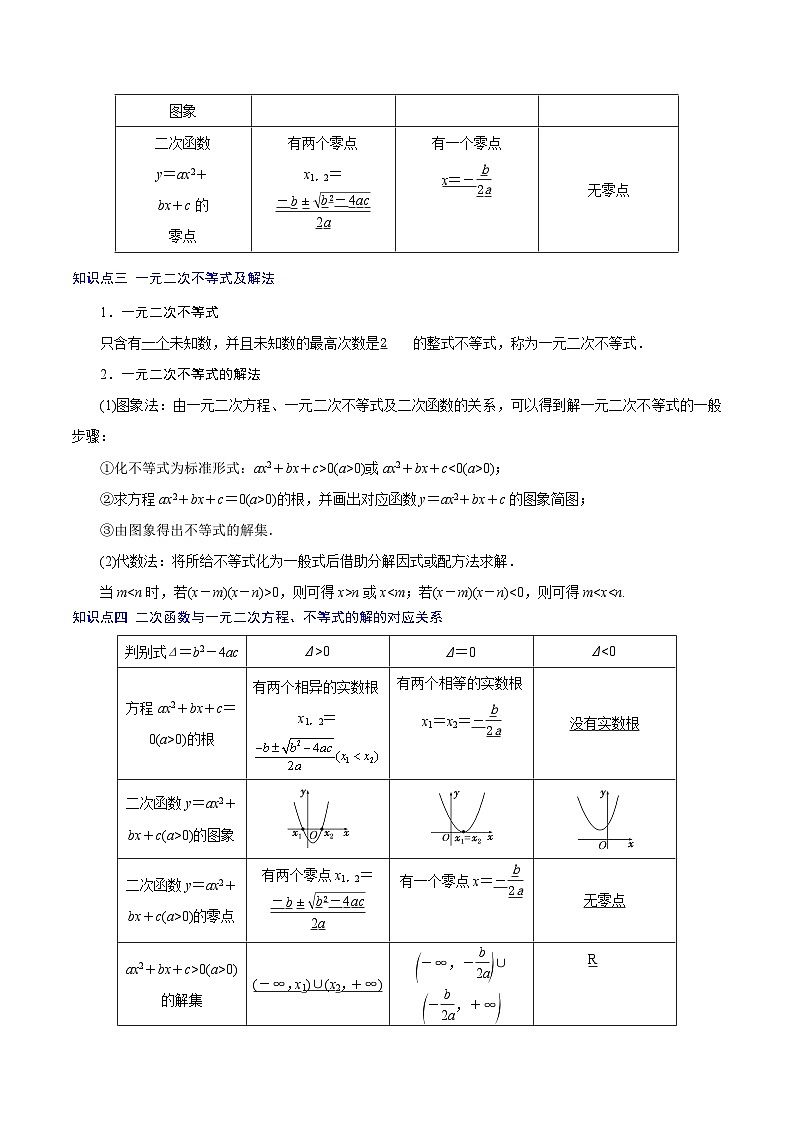
知识点三 一元二次不等式及解法
1．一元二次不等式
只含有一个未知数，并且未知数的最高次数是的整式不等式，称为一元二次不等式．
2．一元二次不等式的解法
(1)图象法：由一元二次方程、一元二次不等式及二次函数的关系，可以得到解一元二次不等式的一般步骤：
①化不等式为标准形式：ax2＋bx＋c>0(a>0)或ax2＋bx＋c<0(a>0)；
②求方程ax2＋bx＋c＝0(a>0)的根，并画出对应函数y＝ax2＋bx＋c的图象简图；
③由图象得出不等式的解集．
(2)代数法：将所给不等式化为一般式后借助分解因式或配方法求解．
当m0，则可得x>n或x 知识点四 二次函数与一元二次方程、不等式的解的对应关系
判别式Δ＝b2－4ac
Δ>0
Δ＝0
Δ<0
方程ax2＋bx＋c＝0(a>0)的根
有两个相异的实数根x1，2＝
有两个相等的实数根x1＝x2＝－
没有实数根
二次函数y＝ax2＋bx＋c(a>0)的图象



二次函数y＝ax2＋bx＋c(a>0)的零点
有两个零点x1，2＝
有一个零点x＝－
无零点
ax2＋bx＋c>0(a>0)的解集
(－∞，x1)∪(x2，＋∞)
∪

ax2＋bx＋c<0(a>0)的解集
(x1，x2)


1．函数的角度：一元二次不等式ax2＋bx＋c>0表示二次函数y＝ax2＋bx＋c的函数值大于0，图象在x轴的上方；一元二次不等式ax2＋bx＋c>0的解集即二次函数图象在x轴上方部分的自变量的取值范围．
2．方程的角度：一元二次不等式ax2＋bx＋c>0的解集的端点值是一元二次方程ax2＋bx＋c＝0的根．


考点一：求二次函数的零点
例1 (1)二次函数y＝x2－7x＋12的零点为________；
(2)若函数y1＝x2－ax－b的图象如图所示，则函数y2＝bx2－ax－1的零点是________．

【答案】　(1)3和4　(2)－和－
【解析】(1)由x2－7x＋12＝0得x1＝3，x2＝4.
所以函数y＝x2－7x＋12的零点为3和4.
(2)由题图可知函数y1＝x2－ax－b的零点是2和3，由函数的零点与对应方程根的关系知方程x2－ax－b＝0的两根为2和3，再由根与系数的关系得a＝2＋3＝5，－b＝2×3＝6，即a＝5，b＝－6.所以y2＝－6x2－5x－1，易得y2＝－6x2－5x－1的零点为－和－.
【总结】
二次函数零点的求法
(1)代数法：求出方程ax2＋bx＋c＝0(a≠0)的实数根，即为函数y＝ax2＋bx＋c(a≠0)的零点；
(2)几何法：对于不能用求根公式或分解因式求解的方程，可以将它与对应函数的图象联系起来，利用函数的性质求零点．
变式 求下列函数的零点．
(1)y＝3x2－2x－1；
(2)y＝ax2－x－a－1(a∈R)；
(3)y＝ax2＋bx＋c，其图象如图所示．

【解析】(1)由3x2－2x－1＝0解得x1＝1，x2＝－，所以函数y＝3x2－2x－1的零点为1和－.
(2)①当a＝0时，y＝－x－1，由－x－1＝0得x＝－1，所以函数的零点为－1.
②当a≠0时，由ax2－x－a－1＝0得(ax－a－1)(x＋1)＝0，解得x1＝，x2＝－1，
又－(－1)＝.
当a＝－时，x1＝x2＝－1，函数有唯一的零点－1.
当a≠－且a≠0时，x1≠x2，函数有两个零点－1和.
综上，当a＝0或－时，函数的零点为－1.
当a≠－且a≠0时，函数有两个零点－1和.
(3)由图象可知，函数有两个零点－1和3.


考点二：函数的零点个数的判断与证明
例2 若a>2，求证： 函数y＝(a－2)x2－2(a－2)x－4有两个零点．
【证明】因为Δ＝4(a－2)2＋16(a－2)＝4(a－2)(a＋2)，
又a>2，所以Δ>0，
所以方程(a－2)x2－2(a－2)x－4＝0有两个根，故函数y＝(a－2)x2－2(a－2)x－4有两个零点．
【总结】
二次函数y＝ax2＋bx＋c(a≠0)的零点个数的判断
对于一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式Δ＝b2－4ac.
(1)Δ>0⇔函数y＝ax2＋bx＋c(a≠0)有两个零点；
(2)Δ＝0⇔函数y＝ax2＋bx＋c(a≠0)有一个零点；
(3)Δ<0⇔函数y＝ax2＋bx＋c(a≠0)无零点．


变式 （1）求函数y＝(a－2)x2－2(a－2)x－4有零点的充要条件．
【解析】因为函数y＝(a－2)x2－2(a－2)x－4有零点．
当a＝2时，方程(a－2)x2－2(a－2)x－4＝0无解，函数无零点．
当a≠2时，因为函数y＝(a－2)x2－2(a－2)x－4有零点，所以方程(a－2)x2－2(a－2)x－4＝0有实数根．
所以Δ＝4(a－2)2＋16(a－2)＝4(a－2)(a＋2)≥0.
即或
解得a≥2或a≤－2，又a≠2所以a>2或a≤－2，
所以函数y＝(a－2)x2－2(a－2)x－4有零点的充要条件为a>2或a≤－2.
（2）求证：函数y＝ax2－x－a(a∈R)有零点．
【证明】当a＝0时，y＝－x，该函数有零点0；
当a≠0时，对于一元二次方程ax2－x－a＝0，Δ＝1＋4a2>0，函数y＝ax2－x－a有两个零点．
综上，函数y＝ax2－x－a(a∈R)有零点．

考点三：二次函数零点的分布探究
例3 (1)判断二次函数y＝－x2－2x＋1在(－3，－2)是否存在零点；
(2)若二次函数y＝(a－2)x2－2(a－2)x－4(a≠2)的两个零点均为正数，求实数a的取值范围．
【解析】(1)由－x2－2x＋1＝0得x1＝－1＋，x2＝－1－，因为－3<－1－<－2，所以二次函数y＝－x2－2x＋1在(－3，－2)存在零点．
(2)因为函数y＝(a－2)x2－2(a－2)x－4的两个零点均为正数，
所以(a－2)x2－2(a－2)x－4＝0有两个正实数根．显然a≠2.
由一元二次方程的根与系数的关系得即所以a＜－2，
即实数a的取值范围是(－∞，－2).




【总结】
二次函数y＝ax2＋bx＋c(a≠0)零点的分布探究
结合一元二次方程ax2＋bx＋c＝0(a≠0)根的判别式Δ＝b2－4ac和根与系数的关系处理：
(1)⇔函数y＝ax2＋bx＋c(a≠0)有两个正零点；
(2)⇔函数y＝ax2＋bx＋c(a≠0)有两个负零点；
(3)x1x2<0⇔函数y＝ax2＋bx＋c(a≠0)有两个异号零点．
变式 已知函数y＝x2－x－a2＋a(a∈R).
(1)若该函数有两个不相等的正零点，求a的取值范围；
(2)若该函数有两个零点，一个大于1，另一个小于1，求a的取值范围．
【解析】由x2－x－a2＋a＝0得x1＝a，x2＝1－a，
(1)因为该函数有两个不相等的正零点，所以解得0 所以a的取值范围是∪.
(2)因为函数有两个零点，一个大于1，另一个小于1，
所以或解得a>1或a<0.
所以a的取值范围是(－∞，0)∪(1，＋∞).

考点四：不含参数的一元二次不等式的解法
例4 解下列不等式：
(1)2x2＋5x－3<0；(2)－3x2＋6x≤2；(3)4x2＋4x＋1>0.
【解析】(1)Δ＝49>0，方程2x2＋5x－3＝0的两根为x1＝－3，x2＝，
作出函数y＝2x2＋5x－3的图象，如图①所示．
由图可得原不等式的解集为.

(2)原不等式等价于3x2－6x＋2≥0.Δ＝12>0，解方程3x2－6x＋2＝0，得x1＝，x2＝，
作出函数y＝3x2－6x＋2的图象，如图②所示，由图可得原不等式的解集为.
(3)∵Δ＝0，∴方程4x2＋4x＋1＝0有两个相等的实根x1＝x2＝－.作出函数y＝4x2＋4x＋1的图象如图③所示．

由图可得原不等式的解集为{x}．
【总结】
解不含参数的一元二次不等式的方法
方法一：若不等式对应的一元二次方程能够因式分解，即能够转化为两个一次因式乘积的形式，则可以直接由一元二次方程的根及不等号方向得到不等式的解集；
方法二：若不等式对应的一元二次方程能够化为完全平方式，不论取何值，完全平方式始终大于或等于零，不等式的解集易得；
方法三：若上述两种方法均不能解决，则应采用求一元二次不等式的解集的通法，即判别式法．

变式 （1）不等式－2x2＋x＋3<0的解集是(　　)
A．{x|x<－1} B．
C． D．
【答案】D　
【解析】不等式－2x2＋x＋3<0可化为2x2－x－3>0，因为Δ＝(－1)2－4×2×(－3)＝25>0，方程2x2－x－3＝0的两根为x1＝－1，x2＝，又二次函数y＝2x2－x－3的图象开口向上，所以不等式－2x2＋x＋3<0的解集是.故选D.
（2）解不等式：－2 【解析】原不等式等价于不等式组
不等式①可化为x2－3x＋2>0，解得x>2或x<1.
不等式②可化为x2－3x－10≤0，解得－2≤x≤5.
故原不等式的解集为{x|－2≤x<1或2 考点五：含参数的一元二次不等式的解法
例5 　(1)解关于x的不等式ax2－(a＋1)x＋1<0；
(2)已知关于x的不等式(m2＋4m－5)x2－4(m－1)x＋3>0对一切实数x恒成立，求实数m的取值范围．
【解析】(1)①当a＝0时，原不等式即为－x＋1<0，解得x>1.
②当a<0时，原不等式化为(x－1)>0，解得x<或x>1.
③当a>0时，原不等式化为(x－1)<0.
若a＝1，即＝1时，不等式无解；
若a>1，即<1时，解得 若01时，解得1 综上可知，当a<0时，不等式的解集为{x|x<或x>1}；
当a＝0时，不等式的解集为{x|x>1}；
当0 当a＝1时，不等式的解集为∅；
当a>1时，不等式的解集为.
(2)①当m2＋4m－5＝0，即m＝1或m＝－5时，显然m＝1符合条件，m＝－5不符合条件；
②当m2＋4m－5≠0时，由二次函数对一切实数x恒成立，得解得1 综合①②得，实数m的取值范围为{m|1≤m＜19}．
【总结】
含参一元二次不等式的解法

变式 已知函数y＝x2＋bx＋c(b，c∈R)，且y≤0的解集为[－1，2].
(1)求函数y的解析式；
(2)解关于x的不等式m(x2－x－2)>2(x－m－1)(m≥0).
【解析】(1)因为y≤0的解集为[－1，2]，所以x2＋bx＋c＝0的根为－1，2，所以－b＝1，c＝－2，即b＝－1，c＝－2，所以y＝x2－x－2.
(2)由m(x2－x－2)>2(x－m－1)，整理得(mx－2)(x－1)>0，所以当m＝0时，不等式的解集为(－∞，1)；当02时，不等式的解集为∪(1，＋∞).

考点六：一元二次不等式解集逆向应用
例6 (多选)已知不等式ax2＋bx＋c>0的解集为，则下列结论正确的是(　　)
A．a>0 B．b>0
C．c>0 D．a＋b＋c>0
【答案】BCD
【解析】因为不等式ax2＋bx＋c>0的解集为，故相应的二次函数y＝ax2＋bx＋c的图象开口向下，所以a<0，故A错误；易知2和－是方程ax2＋bx＋c＝0的两个根，则有＝－1<0，－＝>0，又a<0，故b>0，c>0，故B、C正确；由题意可知当x＝1时，y＝a＋b＋c>0，故D正确．故选B、C、D.


【总结】
一元二次不等式解集逆向应用问题的解法及步骤
(1)求解方法：由已知不等式的解可转化为一元二次方程的两根，从而由根与系数的关系，找出系数a，b，c之间的关系，写出不等式的解集；
(2)求解步骤
①明确解题方向：如要解cx2＋bx＋a<0，首先确定c的符号，最好能确定a，b，c的值；
②审条件——挖掘题目信息：利用一元二次方程的根与一元二次不等式的解集的关系列出关于a，b，c的方程组，用a表示b，c；
③建联系——找解题突破口：由给定不等式的解集形式→确定关于a，b，c的方程组→用a表示b，c→代入所求不等式→求解cx2＋bx＋a<0的解集．

变式 若不等式ax2－x－c>0的解集为{x|－2
【答案】B　
【解析】因为不等式的解集为{x|－2


1．函数y＝x2－4x＋3的零点为(　　)
A．(1，0) B．(1，3)
C．1和3 D．(1，0)和(3，0)
【答案】C　
【解析】令x2－4x＋3＝0，解得x＝1或x＝3，所以函数的零点为1和3.故选C.
2．函数y＝x2－2x＋2的零点个数是(　　)
A．0 B．1
C．2 D．3
【答案】A　
【解析】令x2－2x＋2＝0，则Δ＝4－8＝－4＜0，所以方程x2－2x＋2＝0无解，即函数f(x)＝x2－2x＋2的零点个数是0.故选A.
3．已知p：关于x的方程ax2＋bx＋c＝0有两个异号实数根，q：ac<－1，则p是q的________条件．
【答案】必要不充分
【解析】因为关于x的方程ax2＋bx＋c＝0有两个异号实数根⇔x1x2＝<0⇔ac<0，所以p是q的必要不充分条件．
4．讨论函数y＝(ax－1)(x－2)(a∈R)的零点．
【解析】当a＝0时，函数为y＝－x＋2，则函数的零点为2；
当a＝时，则(x－2)＝0，解得x1＝x2＝2，则函数的零点为2；
当a≠0且a≠时，由(ax－1)(x－2)＝0，
解得x1＝，x2＝2，则函数的零点为和2.
5．不等式x(x－9)＜x－21的解集为(　　)
A．(3，7) B．(－∞，3)∪(7，＋∞)
C．(－7，－3) D．(－∞，－7)∪(－3，＋∞)
【答案】A　
【解析】∵x(x－9)＜x－21，∴x2－10x＋21＜0，∴(x－3)(x－7)＜0，解得3＜x＜7.故选A.
6．已知a＜0，则关于x的不等式x2－4ax－5a2＜0的解集是(　　)
A．{x|x＞5a或x＜－a} B．{x|x＜5a或x＞－a}
C．{x|－a＜x＜5a} D．{x|5a＜x＜－a}
【答案】D　
【解析】因为方程x2－4ax－5a2＝0的解为x＝－a或5a，且a＜0，所以不等式x2－4ax－5a2＜0的解集是{x|5a＜x＜－a}．故选D.
7．(多选)关于x的不等式ax2＋bx＋c＜0的解集为(－∞，－2)∪(3，＋∞)，则下列正确的是(　　)
A．a＜0
B．关于x的不等式bx＋c＞0的解集为(－∞，－6)
C．a＋b＋c＞0
D．关于x的不等式cx2－bx＋a＞0的解集为∪
【答案】ACD　
【解析】A，由已知可得a＜0且－2，3是方程ax2＋bx＋c＝0的两根，A正确；
B，由根与系数的关系可得解得b＝－a，c＝－6a，则不等式bx＋c＞0可化为－ax－6a＞0，即x＋6＞0，所以x＞－6，B错误；
C，a＋b＋c＝a－a－6a＝－6a＞0，C正确；
D，不等式cx2－bx＋a＞0可化为－6ax2＋ax＋a＞0，即6x2－x－1＞0，解得x＞或x＜－，D正确．
故选A、C、D.
8．写出一个解集为(－2，3)的一元二次不等式________．
【答案】(x＋2)(x－3)＜0(答案不唯一)
【解析】由一元二次不等式的解法可知，解集为(－2，3)的一元二次不等式可以是(x＋2)(x－3)＜0.
9．已知y＝(x－a)(x－2).
(1)当a＝1时，求不等式y＞0的解集；
(2)解关于x的不等式y＜0.
【解析】(1)a＝1时，不等式y＞0化为(x－1)(x－2)＞0，解得x＜1或x＞2，
∴不等式的解集为(－∞，1)∪(2，＋∞).
(2)关于x的不等式y＜0，即(x－a)(x－2)＜0，
当a＝2时，不等式化为(x－2)2＜0，不等式无解；
当a＞2时，解不等式(x－a)(x－2)＜0，得2＜x＜a；
当a＜2时，解不等式(x－a)(x－2)＜0，得a＜x＜2.
综上所述，a＝2时，不等式无解；a＞2时，不等式的解集为(2，a)；a＜2时，不等式的解集为(a，2).


1．若x1，x2是二次函数y＝x2－5x＋6的两个零点，则＋的值为(　　)
A．－ B．－
C．－ D．
【答案】D　
【解析】解一元二次方程x2－5x＋6＝0，即可求得x1＝2，x2＝3，代入可得＋＝＋＝.
2．函数y＝x2－(a＋1)x＋a的零点个数为(　　)
A．1 B．2
C．1或2 D．0
【答案】C　
【解析】由x2－(a＋1)x＋a＝0得x1＝a，x2＝1，当a＝1时函数的零点为1个，当a≠1时，函数的零点有2个．所以该函数的零点个数是1或2.
3．关于x的函数y＝x2－2ax－8a2(a>0)的两个零点为x1, x2，且x2－x1＝15，则a＝(　　)
A． B．
C． D．
【答案】A　
【解析】由条件知x1，x2为方程x2－2ax－8a2＝0的两根，则x1＋x2＝2a，x1x2＝－8a2.
由(x2－x1)2＝(x1＋x2)2－4x1x2＝(2a)2－4×(－8a2)＝36a2＝152，解得a＝.故选A.
4．不等式9x2＋6x＋1≤0的解集是(　　)
A． B．
C．∅ D．
【答案】D　
【解析】原不等式可化为(3x＋1)2≤0，∴3x＋1＝0，∴x＝－.
5．若一元二次不等式kx2－2x＋k＜0的解集为{x|x≠m}，则m＋k的值为(　　)
A．－1 B．0
C．－2 D．2
【答案】C　
【解析】∵不等式kx2－2x＋k＜0的解集为{x|x≠m}，
∴解得k＝－1，m＝－1，故m＋k＝－2.故选C.
6．已知函数y＝x2－6x＋5－m的两个零点都大于2，则实数m的取值范围是(　　)
A．[－4，－3)
B．(－4，－3]
C．(－4，－3)
D．(－∞，－4)∪(－3，＋∞)
【答案】C　
【解析】x2－6x＋5－m＝0的两根都大于2，则二次函数y＝x2－6x＋5－m的图象与x轴的两个交点都在x＝2的右侧，故方程的判别式Δ>0；当x＝2时函数值y>0；函数对称轴x＝3>2.即解得－4 7．(多选)若关于x的一元二次方程(x－2)·(x－3)＝m有实数根x1，x2，且x1 A．当m＝0时，x1＝2，x2＝3
B．m>－
C．当m>0时，2 D．当m>0时，x1<2<3 【答案】ABD　
【解析】对于A，m＝0时，方程为(x－2)(x－3)＝0，解得x1＝2，x2＝3，所以A正确；对于B，将方程整理可得x2－5x＋6－m＝0，由于方程有两个不同的实数根，所以Δ＝25－4(6－m)>0，解得m>－，所以B正确；对于C和D，当m>0时，根据根与系数的关系可得x1＋x2＝5，x1x2＝6－m<6，结合2＋3＝5，2×3＝6即可得出x1<2，x2>3，故C不正确，D正确．
8．若一元二次不等式kx2－2x＋k＜0的解集为{x|x≠m}，则m＋k的值为(　　)
A．－1 B．0
C．－2 D．2
【答案】C　
【解析】∵不等式kx2－2x＋k＜0的解集为{x|x≠m}，
∴解得k＝－1，m＝－1，故m＋k＝－2.故选C.
9．(多选)函数y＝(x－2)(x－4)－1有两个零点x1，x2，且x1＜x2，下列关于x1，x2的关系中错误的有(　　)
A．x1＜2且2＜x2＜4 B．x1＞2且x2＞4
C．x1＜2且x2＞4 D．2＜x1＜4且x2＞4
【答案】ABD　
【解析】令y1＝(x－2)·(x－4)，则y＝y1－1，∴函数y＝(x－2)(x－4)－1的零点就是函数y1＝(x－2)(x－4)与函数y＝1图象交点的横坐标．在同一平面直角坐标系中作出函数y1＝(x－2)(x－4)的图象与y＝1的图象(图略)，结合图象知C正确．故选A、B、D.
10．函数y＝x2＋x＋m的两个零点都是负数，则m的取值范围为________．
【答案】
【解析】因为函数y＝x2＋x＋m的两个零点都是负数，所以解得0 11．求下列函数的零点．
(1)y＝x－2－3；(2)y＝x2－(3a－1)x＋(2a2－2).
【解析】(1)由x－2－3＝0得(＋1)(－3)＝0，
又 ≥0，所以＝3，
即x＝9，所以函数y＝x－2－3的零点为9.
(2)由x2－(3a－1)x＋(2a2－2)＝0得[x－(a＋1)][x－2(a－1)]＝0，
①当a＋1＝2(a－1)，即a＝3时，函数有唯一零点4；
②当a＋1≠2(a－1)，即a≠3时，函数有两个零点a＋1和2(a－1).
12．已知函数y＝ax2＋bx＋1有两个零点x1，x2，则“|a|≥1”是“|x1|＋|x2|≤2”的(　　)
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分又不必要条件
【解析】B　由题意得a≠0，且x1，x2是方程ax2＋bx＋1＝0的两个根，故x1x2＝，所以＝|x1x2|＝|x1|·|x2|≤，当且仅当|x1|＝|x2|时等号成立．若|x1|＋|x2|≤2，则|a|≥1；反之，若|a|≥1，则|x1|·|x2|≤1，当x1＝2，x2＝时，|x1|·|x2|＝＜1，但|x1|＋|x2|＝＞2.故“|a|≥1”是“|x1|＋|x2|≤2”的必要不充分条件．
13．(多选)对于函数y＝ax2－x－2a，下列说法中正确的是(　　)
A．函数一定有两个零点
B．a>0时，函数一定有两个零点
C．a<0时，函数一定有两个零点
D．函数的零点个数是1或2
【解析】BCD　当a≠0时，相应方程ax2－x－2a＝0中Δ＝1＋8a2>0，所以函数一定有两个零点，故B、C正确．当a＝0时，函数有唯一零点为0，故D正确，A不正确．
14．一元二次不等式x2－(a＋1)x＋a＜0(a＞1)的解集中有3个整数，则实数a的取值范围为________．
【答案】(4，5]
【解析】关于x的不等式x2－(a＋1)x＋a＜0可化为(x－1)(x－a)＜0，因为a＞1时，所以1＜x＜a，解集中有3个整数，则必为2，3，4，所以4＜a≤5.故a的取值范围是(4，5].
15．已知函数y＝2ax－a＋3在(－1，1)上有零点，则实数a的取值范围是________________．
【答案】(－∞，－3)∪(1，＋∞)
【解析】当a＝0时，函数y＝3，无零点．当a≠0时，由2ax－a＋3＝0得x＝，所以－1<<1，当a>0时，－2a1；当a<0时，－2a>a－3>2a，解得a<－3.所以实数a的取值范围是(－∞，－3)∪(1，＋∞).
16．解关于x的不等式x2－(3a－1)x＋(2a2－2)>0.
【解析】原不等式可化为[x－(a＋1)][x－2(a－1)]>0.
讨论a＋1与2(a－1)的大小：
当a＋1>2(a－1)，即a<3时，x>a＋1或x<2(a－1).
当a＋1＝2(a－1)，即a＝3时，x≠4.
当a＋1<2(a－1)，即a>3时，x>2(a－1)或x 综上，当a<3时，解集为{x|x>a＋1或x<2(a－1)}；
当a＝3时，解集为{x|x≠4}；
当a>3时，解集为{x|x>2(a－1)或x 17．若函数y＝x2－2ax＋a2－1的两个零点分别为m，n，且m<－1，n>，求实数a的取值范围．
【解析】函数y＝x2－2ax＋a2－1的两个零点分别为m，n，
又x2－2ax＋a2－1＝0的两个实数根为a－1，a＋1.
所以解得－ 18．已知二次函数y＝x2－4x＋2k.
(1)若二次函数y＝x2－4x＋2k有零点，求实数k的取值范围；
(2)如果k是满足(1)的最大整数，且二次函数y＝x2－4x＋2k的零点是二次函数y＝x2－2mx＋3m－1的一个零点，求m的值及二次函数y＝x2－2mx＋3m－1的另一个零点．
【解析】(1)由题意得Δ≥0，∴16－8k≥0，解得k≤2.
(2)由(1)可知k＝2，∴方程x2－4x＋2k＝0的根x1＝x2＝2，二次函数y＝x2－4x＋2k的零点是2，
∴二次函数y＝x2－2mx＋3m－1的一个零点是2，∴方程x2－2mx＋3m－1＝0的一个根为2，
∴4－4m＋3m－1＝0，解得m＝3.∴方程x2－2mx＋3m－1＝x2－6x＋8＝0，
解得x＝2或x＝4.∴二次函数y＝x2－2mx＋3m－1的另一个零点为4.