北师大版九年级上册3 正方形的性质与判定优质课ppt课件

这是一份北师大版九年级上册3 正方形的性质与判定优质课ppt课件，共26页。PPT课件主要包含了学习目标，知识回顾，对边平行且相等，对边平行四边都相等，对角相等邻角互补，四个角都是直角，对角线互相平分，对角线相等且互相平分，中心对称图形，导入新课等内容，欢迎下载使用。
1.理解正方形的概念.2.探索并证明正方形的性质，并了解平行四边形、 矩形、菱形之间的联系和区别.(重点、难点)3.会应用正方形的性质解决相关证明及计算问题. （难点）
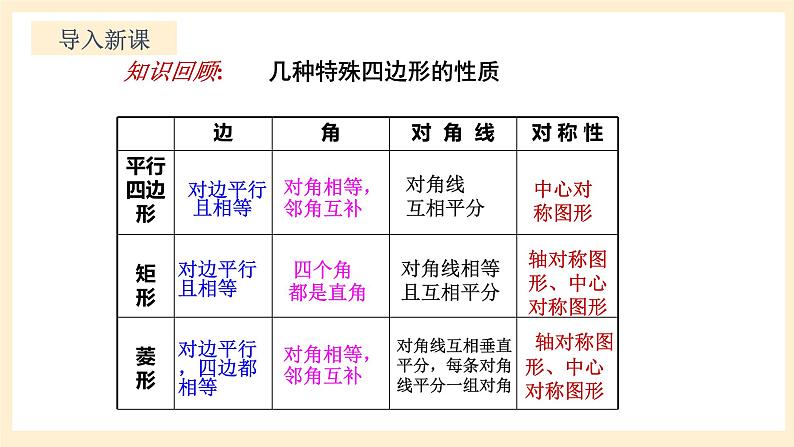
几种特殊四边形的性质
对角线互相垂直平分，每条对角线平分一组对角
轴对称图形、中心对称图形
轴对称图形、中心对称图形
1.有一个角是______的平行四边形叫做矩形。2.有一组邻边______的平行四边形叫做菱形。
有没有一种四边形既是菱形又是矩形呢？
活动:观察这些图片，你什么发现？正方形四条边有什么关系？四个角呢？
问题1：矩形怎样变化后就成了正方形呢?你有什么发现？
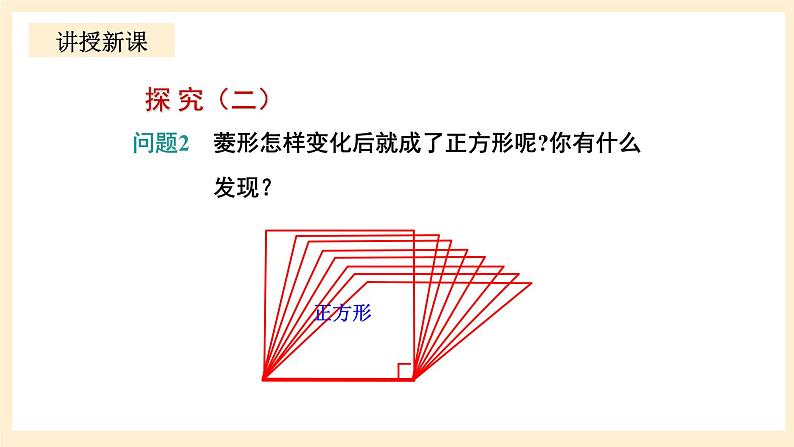
问题2 菱形怎样变化后就成了正方形呢?你有什么 发现？
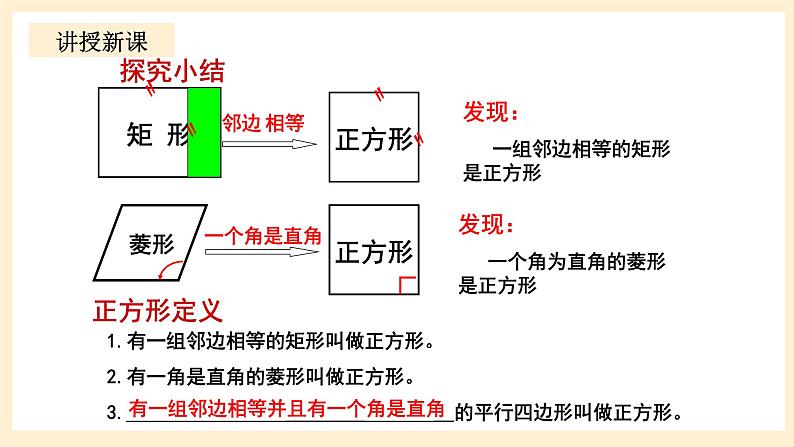
发现： 一组邻边相等的矩形 是正方形
发现： 一个角为直角的菱形是正方形
1.有一组邻边相等的矩形叫做正方形。2.有一角是直角的菱形叫做正方形。3.________________ _________的平行四边形叫做正方形。
有一组邻边相等并且有一个角是直角
平行四边形、矩形、菱形、正方形的关系
二、正方形的性质探究和证明
猜想：正方形是特殊的矩形，也是特殊的菱形。
填一填：角： 边：对角线： 对称性：
对角线相等且互相垂直平分.
轴对称图形（4条对称轴）.
1.正方形的四个角都是直角,四条边相等.2.正方形的对角线相等且互相垂直平分.
已知：如右图,四边形ABCD是正方形.求证：正方形ABCD四边相等,四个角都是直角.
证明：∵四边形ABCD是正方形.∴∠A=90°, AB=AC . （正方形的定义）又∵正方形是平行四边形.∴正方形是矩形, （矩形的定义） 正方形是菱形.(菱形的定义)∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD.
已知：如右图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证：AO=BO=CO=DO,AC⊥BD.
请同学们动手完成以上证明？
提示：可以先通过证明来得到正方形是矩形、菱形，然后利用矩形和菱形的定理来完成该题.
轴对称图形（4条对称轴）
例1：如图在正方形ABCD中,E为CD上一点，F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系？请说明理由.
解：BE=DF,且BE⊥DF.理由如下：（1）∵四边形ABCD是正方形.∴BC=DC,∠BCE =90° .（正方形的四条边都相等,四个角都是直角）∴∠DCF=180°-∠BCE=180°-90°=90°.
∴∠BCE=∠DCF.又∵CE=CF.∴△BCE≌△DCF.∴BE=DF.(2)延长BE交DE于点M,∵△BCE≌△DCF ,∴∠CBE =∠CDF.∵∠DCF =90° ,∴∠CDF +∠F =90°.∴∠CBE+∠F=90° , ∴∠BMF=90°.∴BE⊥DF.
例2：如图，已知四边形ABCD是正方形,对角线AC与BD相交于点O , MN∥AB ,且分别于OA , OB相交于点M , N.求证：（1）BM = CN;（2）BM⊥CN.
证明：（1）∵MN∥AB. ∴∠1 =∠2 =∠3 =∠4 = 45°. ∴OM = ON. ∵OA= OB, ∴OA- OM = OB - ON,AM=BN. 又∵∠2=∠NBC,AB=BC. ∴△ABM ≌△BCN(SAS) ∴BM=CN.
(2)延长CN交线段MB于点Q.∵△ABM≌△BCN.∴∠6=∠8.∵∠OCB =∠ABO =45°.∴∠5=∠7.又∵∠ONC=∠QNB.∴180°-∠5 -∠ONC = 180°-∠7 -∠QNB,∠CON =∠NQB = 90°.∴BM⊥CN.
对边平行， 四条边 都相等
对角线互相垂直平分且相等，每条对角线平分一组对角
2.一个正方形的对角线长为2cm，则它的面积是 （　　）A.2cm2 B.4cm2 C.6cm2 D.8cm2
1.平行四边形、矩形、菱形、正方形都具有的是（　） A．对角线互相平分 B．对角线互相垂直 C．对角线相等 D．对角线互相垂直且相等
3．在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .4.在正方形ABCD中，E是对角线AC上一点，且AE=AB，则∠EBC的度数是 .
5.如图，已知正方形ABCD ,以AB为边向正方形外作等边△ABE,连结DE 、 CE ,求∠DEC的度数.
解：∵△ABE是等边三角形. ∴AB =AE=BE, ∠ABE=∠BEA=∠EAB =60°. 又∵四边形ABCD是正方形. ∴AD=BC=AE=BE, ∠DAB=∠ABC=90°. ∴∠DAE=∠CBE=150°. ∴∠AED=∠EDA=∠CEB=∠BCE=15°. ∴∠DEC=∠AEB-∠AED-∠CEB=30°.
6.如图，四边形ABCD是正方形，对角线AC与BD相交于点O，AO＝2，求正方形的周长与面积．
解：∵四边形ABCD是正方形，∴AC⊥BD，OA＝OD＝2.在Rt△AOD中，由勾股定理，得∴正方形的周长为4AD＝ ， 面积为AD2＝8.
7.如图，正方形ABCD的边长为1cm，AC为对角线，AE平分∠BAC，EF⊥AC，求BE的长．
解：∵四边形ABCD为正方形，∴∠B＝90°，∠ACB＝45°，AB＝BC＝1cm.∵EF⊥AC，∴∠EFA＝∠EFC＝90°.又∵∠ECF＝45°，∴△EFC是等腰直角三角形，∴EF＝FC.∵∠BAE＝∠FAE，∠B＝∠EFA＝90°，AE＝AE，∴△ABE≌△AFE，∴AB＝AF＝1cm，BE＝EF.∴FC＝BE.在Rt△ABC中，∴FC＝AC－AF＝( －1)cm，∴BE＝( －1)cm．
3.对角线相等且互相垂直平分
有一组邻相等，并且有一个角是直角的平行四边形叫做正方形