初中数学北师大版九年级上册1 认识一元二次方程完整版ppt课件

这是一份初中数学北师大版九年级上册1 认识一元二次方程完整版ppt课件，共19页。PPT课件主要包含了学习目标，一元二次方程的定义，导入新课，二次项系数，一次项系数，常数项，一元二次方程的根，和-2，概念学习，练一练等内容，欢迎下载使用。
1.理解方程的解的概念.2.经历对一元二次方程解的探索过程并理解其意义.(重点)3.会估算一元二次方程的解.（难点）
经过变形后，只含有一个未知数，并且未知数的次数是二次，这样的整式方程叫一元二次方程
2一元二次方程的一般形式：
ax2+bx+c=0   (a≠0 ，a，b，c 为常数 )
3方程ax2+bx+c=0的条件：
（1）当a≠0时，是一元二次方程。
（2）当a=0并且b≠0 时 ，是一元一次方程。
4．指出下列方程的二次项系数，一次项系数及常数项．（1）2x2―x+1=0 （2）―x2+1=0（3）x2―x=0 　 （4）―x2=0
（1） 2 -1 1（2） -1 0 1（3） 1 -1 0（4） -1 0 0
5.什么叫方程的解，什么叫解方程？
方程的解就是符合方程的未知数的值．求方程的解的过程叫做解方程．
这节课我们通过估算的方法探索方程的解的大致范围．
一元二次方程的根：使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解（又叫做根）.
下面哪些数是方程 x2 – x – 6 = 0 的解? -4 ,-3 , -2 ,-1 ,0 ,1,2,3 ,4
你注意到了吗？一元二次方程可能不止一个根.
例1：已知a是方程 x2+2x－2=0 的一个实数根, 求 2a2+4a +2017的值.
方法总结：已知解求代数式的值，先把已知解代入，再注意观察，有时需运用到整体思想，求解时，将所求代数式的一部分看作一个整体，再用整体思想代入求值．
例2：在上一课中，我们知道四周未铺地毯部分的宽度x满足方程2x2 - 13x + 11 = 0，你能求出这个宽度吗？
二、一元二次方程解的估算
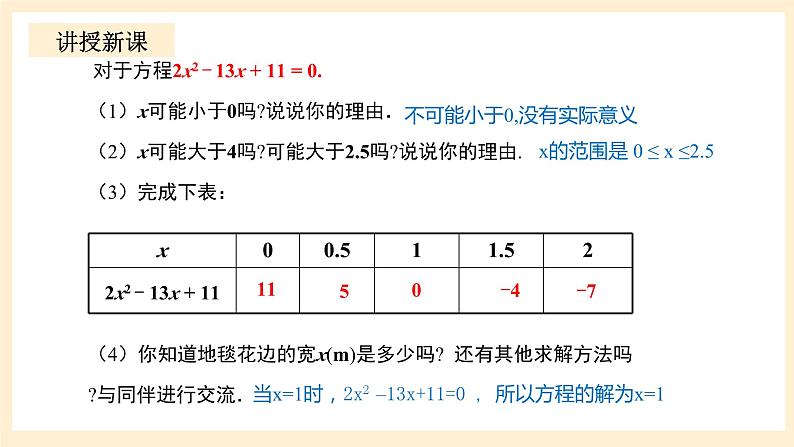
对于方程2x2 - 13x + 11 = 0.（1）x可能小于0吗?说说你的理由． （2）x可能大于4吗?可能大于2.5吗?说说你的理由.（3）完成下表：（4）你知道地毯花边的宽x(m)是多少吗? 还有其他求解方法吗?与同伴进行交流．
不可能小于0,没有实际意义
x的范围是 0 ≤ x ≤2.5
当x=1时，2x2 –13x+11=0 ，所以方程的解为x=1
例3：在上一课中，梯子的底端滑动的距离x满足方程x2 +12 x - 15 = 0.
你能猜出滑动距离x的大致范围吗？
二：下面是小亮的求解过程(取值计算,逐步逼近)：
可知x取值的大致范围是:1