




北师大版4 探索三角形相似的条件优质课件ppt
展开1.知道并理解黄金分割的定义,熟记黄金比;2.能对黄金分割进行简单运用.(重点、难点)
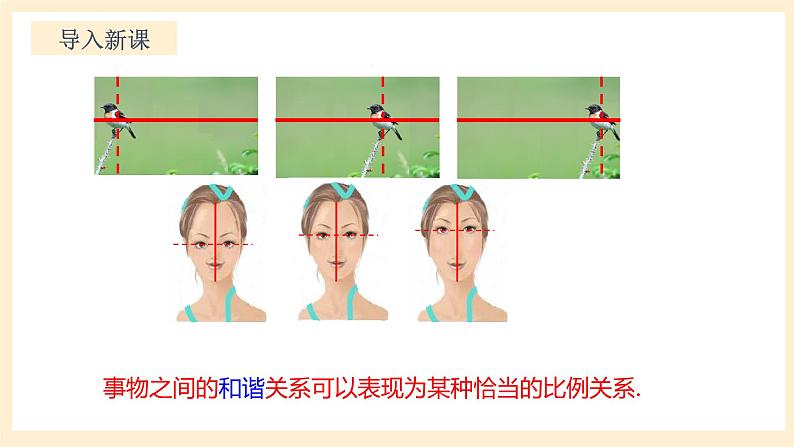
通过观察,你觉得下面那副图最有美感?
事物之间的和谐关系可以表现为某种恰当的比例关系.
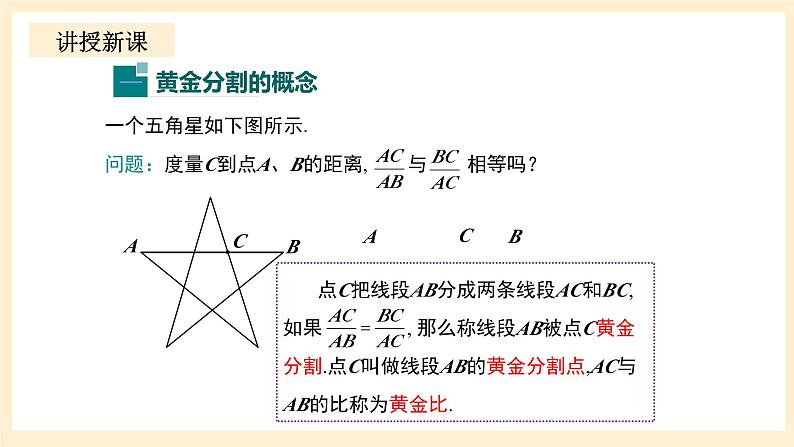
一个五角星如下图所示.问题:度量C到点A、B的距离, 与 相等吗?
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
解:由 ,得AC2 = AB·BC. 设AB = 1,AC = x,则BC = 1 – x. ∴ x2 = 1 ×(1 - x).即 x2 + x – 1 = 0.解方程得:x1= x2=黄金比
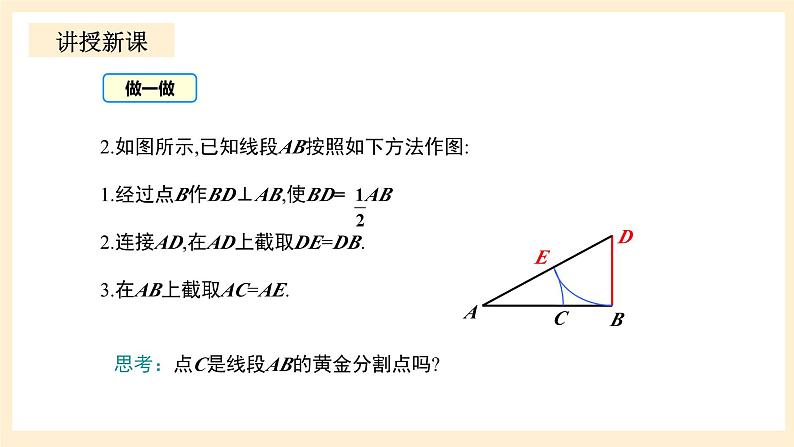
2.如图所示,已知线段AB按照如下方法作图:1.经过点B作BD⊥AB,使BD= AB2.连接AD,在AD上截取DE=DB.3.在AB上截取AC=AE.
思考:点C是线段AB的黄金分割点吗?
巴台农神庙(Parthenm Temple)
点E是AB的黄金分割点
(即 )是黄金比
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形.
例1:在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得 ,解得x = 0.96. 设穿上 y m高的高跟鞋看起来会更美,则 解得 y≈0.075,而0.075m=7.5cm.故她应该穿约为7.5cm高的高跟鞋看起来会更美.
人的俊美,体现在头部及躯干是否符合黄金分割. 美神维纳斯,她身体的各个部位都暗藏比例0.618,虽然雕像残缺,却能仍让人叹服她不可言喻的美.
黄金分割,尤其宽与长的比为黄金比的矩形,在古典及现代建筑中都有广泛的应用.
在人的面部,五官的分布越符合黄金分割,看起来就越美.
Apple lg苹果中小叶子的高度和缺口的高度比是0.6,而缺口的位置也和黄金分割有着千丝万缕的关系。也许这里面还有更多黄金的分割的密码,这里就要同学们自己去发现。
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边长与高这比都接近于0.618.
古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.
著名画家达•芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用。通过下面两幅图片可以看出来,蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割,使得这幅油画看起来是那么的和谐和完美.
打开地图,你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”,产地在安徽的祁门,也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰,名川秀水的黄山,庐山,九寨沟等等。衔远山,吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。
蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618; 节目主持人报幕,绝对不会站在舞台的中央,而总是站在舞台的1/3处,站在舞台上侧近于0.618的位置才是最佳的位置; 生活中用的纸为黄金矩形,这样的长方形让人看起来舒服顺眼,正规裁法得到的纸张,不管其大小,如对于、8开、16开、32开等,都仍然是近似的黄金矩形。
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
1.已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形面积为S2,则S1与S2的关系是 ( )A.S1>S2 B.S1
2.点C是线段AB的黄金分割点,如果AB=4,求线段 AC的长度.
AC=4×0.618=2.472 或者 AC=4×(1-0.618)=1.518
离地面的高度 h=3×0.618=1.854m
4. 如图:在△ABC中,AB=AC, ∠BAC=36°, BD平分∠ABC交AC于点D, 求证:D是AC的黄金分割点.
证明:在等腰△ABC中,顶角∠A=36°,所以∠ABC=∠C=72°,∵BD为∠ABC的平分线,∴∠ABD=∠DBC=36°,在△ACB和△BCD中,∠BDC=72°∵∠C=∠C,∠A=∠CBD=36°,∴△ACB∽△BCD,∴AC:BC=BC:DC;∵∠A=∠ABD,∴AD=BD.
∵∠DBC=36°,∠C=72°,∴∠BDC=72°,∴BD=BC,∴AD=BC,∴AC:AD=AD:DC;即点D是AC的黄金分割点.
4.如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.
解: 设AB=1,那么在 Rt△BAE 中,
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
初中数学4 探索三角形相似的条件示范课课件ppt: 这是一份初中数学4 探索三角形相似的条件示范课课件ppt,共20页。PPT课件主要包含了学习目标,情景引入,一个五角星如图所示,典例精析,例1计算黄金比,即x2+x-1=0,解这个方程得,不合题意舍去,则BC=1-x,想一想等内容,欢迎下载使用。
初中数学北师大版九年级上册4 探索三角形相似的条件获奖ppt课件: 这是一份初中数学北师大版九年级上册4 探索三角形相似的条件获奖ppt课件,文件包含核心素养目标444《探索三角形相似的条件》课件pptx、核心素养目标444《探索三角形相似的条件》教案docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学4 探索三角形相似的条件教案配套课件ppt: 这是一份初中数学4 探索三角形相似的条件教案配套课件ppt,共18页。PPT课件主要包含了学习目标,情境导入,探索交流,一个五角星如图所示,例题解析,例1计算黄金比,即x2+x-1=0,解这个方程得,不合题意舍去,则BC=1-x等内容,欢迎下载使用。













