人教版九年级数学上册24.3正多《边形和圆》PPT课件+教案+学案+练习

24.3正多边形和圆当堂达标题

一、选择题

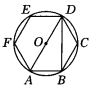
    1．如图1所示，正六边形ABCDEF内接于⊙O，则∠ADB的度数是（   ）．

A．60°    B．45°    C．30°    D．22．5°

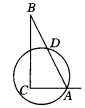
             (1)                    (2)                   (3)

    2．圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（   ）．

      A．36°    B．60°    C．72°     D．108°

    3．若半径为5cm的一段弧长等于半径为2cm的圆的周长，则这段弧所对的圆心角为（   ）．

      A．18°     B．36°    C．72°    D．144°

二、填空题

    1．已知正六边形边长为a，则它的内切圆面积为_______．

    2．在△ABC中，∠ACB=90°，∠B=15°，以C为圆心，CA长为半径的圆交AB于D，如图2所示，若AC=6，则AD的长为________．

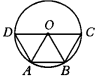
    3．四边形ABCD为⊙O的内接梯形，如图3所示，AB∥CD，且CD为直径，如果⊙O的半径等于r，∠C=60°，那图中△OAB的边长AB是______；△ODA的周长是_______；∠BOC的度数是________．

三、解答题

1．等边△ABC的边长为a，求其内切圆的内接正方形DEFG的面积．

2．如图所示，已知⊙O的周长等于6cm，求以它的半径为边长的正六边形ABCDEF的面积．

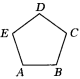
    3．如图所示，正五边形ABCDE的对角线AC、BE相交于M．

    （1）求证：四边形CDEM是菱形；

    （2）设MF2=BE·BM，若AB=4，求BE的长．

24.3正多边形和圆当堂达标题答案

一、1．C  2．C  3．D

二、1．a2  2．  3．r  3r  60°

三、1．设BC与⊙O切于M，连结OM、OB，

则OM⊥BC于M，OM=a，

连OE，作OE⊥EF于N，则OE=OM=a，∠EOM=45°，OE=a，

∵EN=a，EF=2EN=a，∴S正方形=a2．

2．设正六边形边长为a，则圆O半径为a，

由题意得：2a=6，∴a=3．

如右图，设AB为正六边形的一边，O为它的中心，

过O作OD⊥AB，垂足为D，

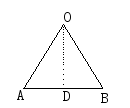
则OD=r6，则∠DOA==30°，AD=AB=，

在Rt△ABC中，OD=r6=cm，

∴S=6·ar6=×3××6=cm2．

3．略.