人教版九年级数学上册24.3 《正多边形和圆》教案

这是一份人教版九年级数学上册24.3 《正多边形和圆》教案，共5页。

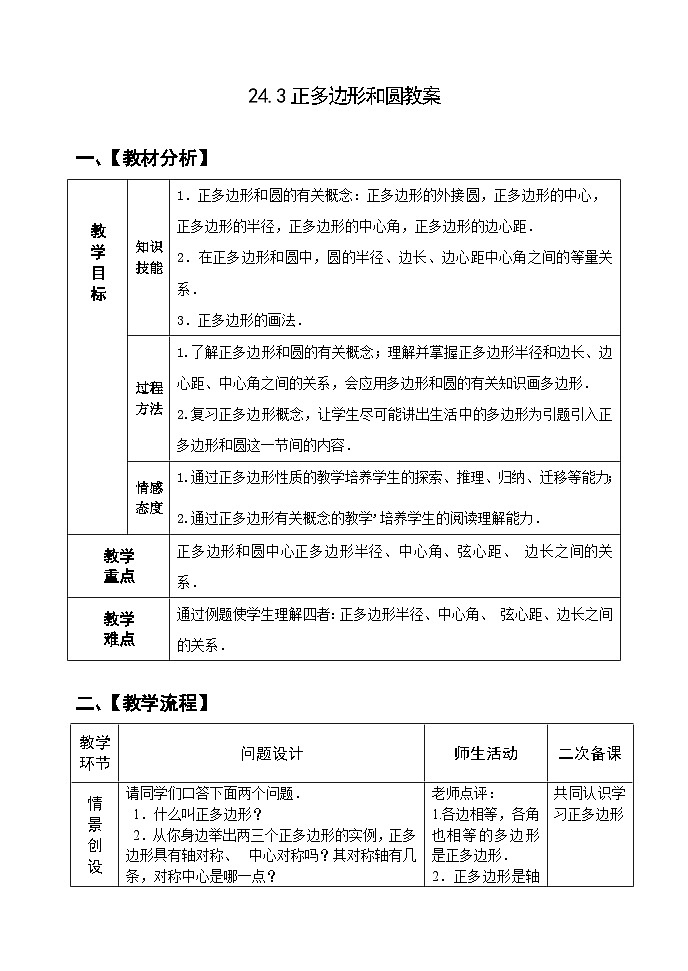
24.3正多边形和圆教案

一、【教材分析】


教
学
目
标
知识
技能
1．正多边形和圆的有关概念：正多边形的外接圆，正多边形的中心，正多边形的半径，正多边形的中心角，正多边形的边心距．
2．在正多边形和圆中，圆的半径、边长、边心距中心角之间的等量关系．
3．正多边形的画法．
过程
方法
1.了解正多边形和圆的有关概念；理解并掌握正多边形半径和边长、边心距、中心角之间的关系，会应用多边形和圆的有关知识画多边形．
2.复习正多边形概念，让学生尽可能讲出生活中的多边形为引题引入正多边形和圆这一节间的内容．
情感
态度
1.通过正多边形性质的教学培养学生的探索、推理、归纳、迁移等能力；
2.通过正多边形有关概念的教学培养学生的阅读理解能力．
教学
重点
正多边形和圆中心正多边形半径、中心角、弦心距、边长之间的关系．
教学
难点
通过例题使学生理解四者：正多边形半径、中心角、弦心距、边长之间的关系．

二、【教学流程】
教学环节
问题设计
师生活动
二次备课
情
景
创
设
请同学们口答下面两个问题．
1．什么叫正多边形？
2．从你身边举出两三个正多边形的实例，正多边形具有轴对称、中心对称吗？其对称轴有几条，对称中心是哪一点？

老师点评：
1.各边相等，各角也相等的多边形是正多边形．
2．正多边形是轴对称图形，对称轴有无数多条；正多边形是中心对称图形，其对称中心是正多边形对应顶点的连线交点．

共同认识学习正多边形
自
主
探
究
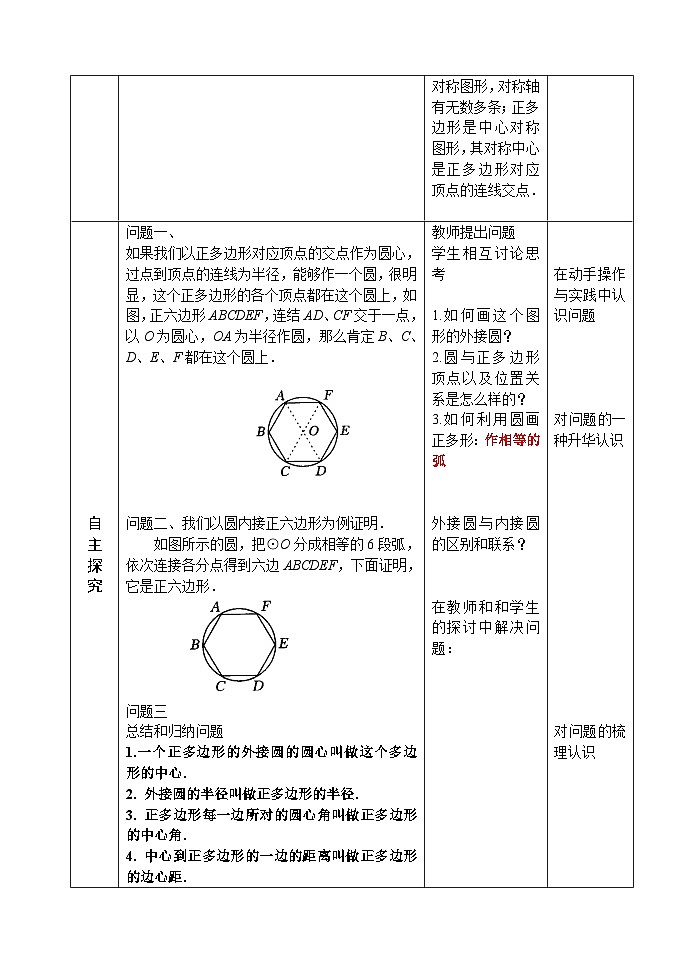
问题一、
如果我们以正多边形对应顶点的交点作为圆心，过点到顶点的连线为半径，能够作一个圆，很明显，这个正多边形的各个顶点都在这个圆上，如图，正六边形ABCDEF，连结AD、CF交于一点，以O为圆心，OA为半径作圆，那么肯定B、C、D、E、F都在这个圆上．







问题二、我们以圆内接正六边形为例证明．
如图所示的圆，把⊙O分成相等的6段弧，依次连接各分点得到六边ABCDEF，下面证明，它是正六边形．





问题三
总结和归纳问题
1.一个正多边形的外接圆的圆心叫做这个多边形的中心．
2. 外接圆的半径叫做正多边形的半径．
3. 正多边形每一边所对的圆心角叫做正多边形的中心角．
4. 中心到正多边形的一边的距离叫做正多边形的边心距．

教师提出问题
学生相互讨论思考

1.如何画这个图形的外接圆？
2.圆与正多边形顶点以及位置关系是怎么样的？
3.如何利用圆画正多形：作相等的弧


外接圆与内接圆的区别和联系？


在教师和和学生的探讨中解决问题：




在动手操作与实践中认识问题




对问题的一种升华认识













对问题的梳理认识
尝
试
应
用
1．已知正六边形ABCDEF，如图所示，其外接圆的半径是a，求正六边形的周长和面积．






2. 利用正多边形的概念和性质来画正多边形，利用手中的工具画一个边长为3cm的正五边形（1）画法（2）步骤




3. 巩固训练
教材P106 练习1、2、3 P108 探究题、练习．
教师提出问题
学生独立思考解答并板书





师生探讨分析：要画正五边形，首先要画一个圆，然后对圆五等分，因此，应该先求边长为3的正五边形的半径

可选做，学生独立完成
一种成果的展示






探讨正多边形的画法


补
偿
提
高
1．在直径为AB的半圆内，划出一块三角形区域，如图所示，使三角形的一边为AB，顶点C在半圆圆周上，其它两边分别为6和8，现要建造一个内接于△ABC的矩形水池DEFN，其中D、E在AB上，如图24-94的设计方案是使AC=8，BC=6．
（1）求△ABC的边AB上的高h．
（2）设DN=x，且，当x取何值时，水池DEFN的面积最大？
（3）实际施工时，发现在AB上距B点1．85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为了保护大树，请设计出另外的方案，使内接于满足条件的三角形中欲建的最大矩形水池能避开大树．
_
h
_
F
_
D
_
E
_
C
_
B
_
A
_
N
_
G

解：（1）由AB·CG=AC·BC得h==4.8
（2）当x=2.4时，SDEFN最大
（3）当SDEFN最大时，x=2.4，此时，F为BC中点，在Rt△FEB中，EF=2.4，BF=3．
∴BE==1.8
∵BM=1.85，∴BM>EB，即大树必位于欲修建的水池边上，应重新设计方案．
∵当x=2.4时，DE=5∴AD=3.2，
由圆的对称性知满足条件的另一设计方案，如图所示:


让学生课堂讨论分析：要求矩形的面积最大，先要列出面积表达式，再考虑最值的求法，初中阶段，尤其现学的知识，应用配方法求最值．（3）的设计要有新意，应用圆的对称性就能圆满解决此题







对不同能力学生的升华认识
小
结
作
业
小结:
通过本节课的学习.你有那些收获?

本节课应掌握：
1．正多边和圆的有关概念：正多边形的中心，正多边形的半径，正多边形的中心角，正多边的边心距．
2．正多边形的半径、正多边形的中心角、边长、正多边的边心距之间的等量关系．
3．画正多边形的方法．
4．运用以上的知识解决实际问题．
作业：
1. P106练习2. 3
P108习题24.3第2题，第6题
2．圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（ ）．
A．36° B．60° C．72° D．108°
3．若半径为5cm的一段弧长等于半径为2cm的圆的周长，则这段弧所对的圆心角为（ ）
A．18° B．36° C．72° D．144°

教师提出问题,
学生独立思考解答.










2．C


3．D

使学生能够回顾，梳理所学知识






增强认识，强化习惯
三、【板书设计】
24.3 正多边形和圆
1.一个正多边形的外接圆的圆心叫做这个多边形的中心．
2. 外接圆的半径叫做正多边形的半径．
3. 正多边形每一边所对的圆心角叫做正多边形的中心角．
4. 中心到正多边形的一边的距离叫做正多边形的边心距．

四、【教后反思】
《正多边形与圆》这一节的教学目标是：让学生能将正多边形的有关计算问题转化为解直角三角形的问题来解决；会用量角器或尺规等分圆、画出正多边形.通过学习使学生能认识到事物之间是普遍联系的，事物之间是可以相互转化的，并培养和训练学生的综合运用知识能力和解决实际问题的能力，渗透数形结合的思想和方法.