人教版九年级上册第二十三章 旋转23.2 中心对称23.2.3 关于原点对称的点的坐标精品导学案

23.2.2 中心对称图形学案

【学习目标】

1.了解中心对称图形的概念及中心对称图形的对称中心的概念，掌握这两个概念的应用．

2.利用这个所学知识探索一个图形是中心对称图形的有关概念及其它的运用．．

【重点难点】

重点：中心对称图形的定义及其性质

难点：中心对称图形与轴对称图形的区别

【新知准备】

1.什么是中心对称？它有怎样的性质？

2.欣赏图片

【课堂探究】

一、自主探究

探究1

（1）将线段AB绕它的中点旋转180°，你有什么发现？

 （2）将平行四边形ABCD绕它的两条对角线的交点旋转180°，你有什么发现？

 （3）你知道什么是中心对称图形吗？请写出它及其有关概念.   

探究2

中心对称与中心对称图形有什么区别与联系？小组讨论交流并以表格的形式总结下来.

二、尝试应用

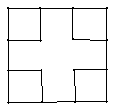在正方形的4个角上剪去4个相同的小正方形（如右图），剩余部分是中心对称图形吗？如果是，画出它们的对称中心.

三、补偿提高

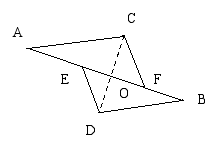
如图, AC=BD，∠A=∠B，点E、F在AB上，且DE∥CF，试说明图形是中心对称图形的理由.xk.C。

[来源:Z*xx*k.Com][来源:Zxxk.Com]

【学后反思】

1.通过本节课的学习你有那些收获?

2. 你还有哪些疑惑？

                               学案答案

一、自主探究

探究1

（1）重合（2）重合（3）如果一个图形绕一个点旋转180°后，能和原来的图形互相重合，那么这个图形叫做中心对称图形；这个点叫做它的对称中心；互相重合的点叫做对称点.

探究2

（略）

二．尝试应用

是中心对称图形

三、补偿提高

连接CD，证明ΔAOC≌ΔBOD.得出AO=BO,CO=DO;再证ΔCOF≌ΔDOE，得出EO=FO.所以该图形是中心对称图形.