人教版九年级上册24.2.2 直线和圆的位置关系优质第3课时导学案及答案

24.2.2 直线和圆的位置关系学案

【学习目标】

1.切线长概念.切线长定理；

2.三角形内切圆以及三角形内心的概念；

3.理解和灵活运用切线长定理以及应用内切圆知识发展解决实际问题能力.

【重点难点】

重点：切线长定理及应用.

难点：应用切线长定理解决问题.

【课堂探究】

一、自主探究

问题一、

切线长概念

如图，P是⊙O外一点，PA，PB是⊙O的两条切线，我们把线段PA，PB叫做点P到⊙O的切线长．

1. 切线长定理

从⊙O外一点P引⊙O的两条切线，切点分别为A、B，那么线段PA和PB之间有何关系？探索步骤：

（1）根据条件画出图形；

（2）度量线段PA和PB的长度；

（3）猜想：线段PA和PB之间的关系；

（4）寻找证明猜想的途径；

（5）在图3中还能得出哪些结论？并把它们归类.

（6）上述各结论中，你想把哪个结论作为切线长的性质？请说明理由.

4、填空：

如图3，PA、PB分别与⊙O相切于点A、B，

（1）若PB=12，PO=13，则AO=＿＿＿.

（2）若PO=10，AO=6，则PB=＿＿＿；

（3）若PA=4，AO=3，则PO=＿＿＿；PD=＿＿；

5、已知如图4，PA、PB分别与⊙O相切于点A、B，

PO与⊙O相交于点D，且PA=4cm,PD=2cm.求半径OA的长.

二、尝试应用

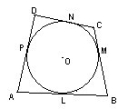
1.证明圆的外切四边形的两组对边的和相等.

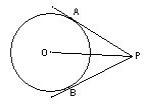
2.填空：如图,已知⊙O的半径为3厘米，PO＝6厘米，PA，PB分别切⊙O于A，B，则PA＝_______，∠APB＝________

3.　已知：在△ABC中，BC＝14厘米，AC＝9厘米，AB＝13厘米，它的内切圆分别和BC，AC，AB切于点D，E，F，求AF，AD和CE的长．

三、补偿提高

1.已知：如图5，⊙O是△ABC的内切圆，切点分别为D、E、F，

（1）图中共有几对相等线段？

（2）若AD=4，BC=5，CF=6，

则△ABC的周长是＿＿；

（3）若AB=4，BC=5，AC=6，

则AD=＿＿，BE=＿＿，CF=＿＿.

2. 在△ABC中，BC=14cm，AC=9cm，AB=13cm，它的内切圆分别和BC、AC、AB切于点D、E、F，求AF、BD、CE的长．

四、小结与作业小结:

通过本节课的学习你学会了哪些知识，会了那些方法？还有哪些疑惑吗？

作业：

  1. 书100页练习1、 2

  2. 补充思考：

如图，有一张四边形ABCD纸片，

且AB=AD=6cm，CB=CD=8cm，

∠B=90°．

（1）要把该四边形裁剪成一个面积最大的圆形纸片，你能否用折叠的方法找出圆心，

若能请你度量出圆的半径（精确到0.1cm）；

（2）计算出最大的圆形纸片的半径（要求精确值）．