人教版九年级数学上册24.3 《正多边形和圆》学案

这是一份人教版九年级数学上册24.3 《正多边形和圆》学案，共2页。
24.3 正多边形和圆学案 【学习目标】1．正多边形和圆的有关概念：正多边形的外接圆，正多边形的中心，正多边形的半径，正多边形的中心角，正多边形的边心距．    2．在正多边形和圆中，圆的半径、边长、边心距中心角之间的等量关系．    3．正多边形的画法． 【重点难点】重点:正多边形和圆中心正多边形半径、中心角、弦心距、边长之间的关系．难点:通过例题使学生理解四者：正多边形半径、中心角、弦心距、边长之间的关系． 【课堂探究】一、自主探究问题一、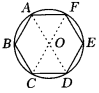如果我们以正多边形对应顶点的交点作为圆心，过点到顶点的连线为半径，能够作一个圆，很明显，这个正多边形的各个顶点都在这个圆上，如图，正六边形ABCDEF，连结AD、CF交于一点，以O为圆心，OA为半径作圆，那么肯定B、C、D、E、F都在这个圆上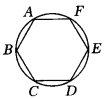． 问题二、我们以圆内接正六边形为例证明．如图所示的圆，把⊙O分成相等的6段弧，依次连接各分点得到六边ABCDEF，下面证明，它是正六边形．  问题三总结和归纳问题  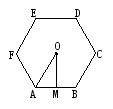  二、尝试应用1．已知正六边形ABCDEF，如图所示，其外接圆的半径是a，求正六边形的周长和面积．  2. 利用正多边形的概念和性质来画正多边形，利用手中的工具画一个边长为3cm的正五边形（1）画法（2）步骤 3. 巩固训练教材P108  练习1、2、  P119  探究题、练习．三、补偿提高1．在直径为AB的半圆内，划出一块三角形区域，如图所示，使三角形的一边为AB，顶点C在半圆圆周上，其它两边分别为6和8，现要建造一个内接于△ABC的矩形水池DEFN，其中D、E在AB上，如图24-94的设计方案是使AC=8，BC=6．    （1）求△ABC的边AB上的高h．    （2）设DN=x，且，当x取何值时，水池DEFN的面积最大？（3）实际施工时，发现在AB上距B点1．85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为了保护大树，请设计出另外的方案，使内接于满足条件的三角形中欲建的最大矩形水池能避开大树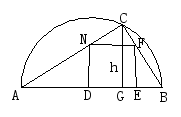．四、小结与作业1.小结:通过本节课的学习.你有那些收获?2.作业：（1）P106练习2.3 P108习题24.3第2题，第6题（2）圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（  ）．A．36°B．60°C．72°     D．108°3．若半径为5cm的一段弧长等于半径为2cm的圆的周长，则这段弧所对的圆心角为（  ）．A．18°B．36°C．72°    D．144°