2022-2023学年广东省惠州市博罗县八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年广东省惠州市博罗县八年级（下）期末数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
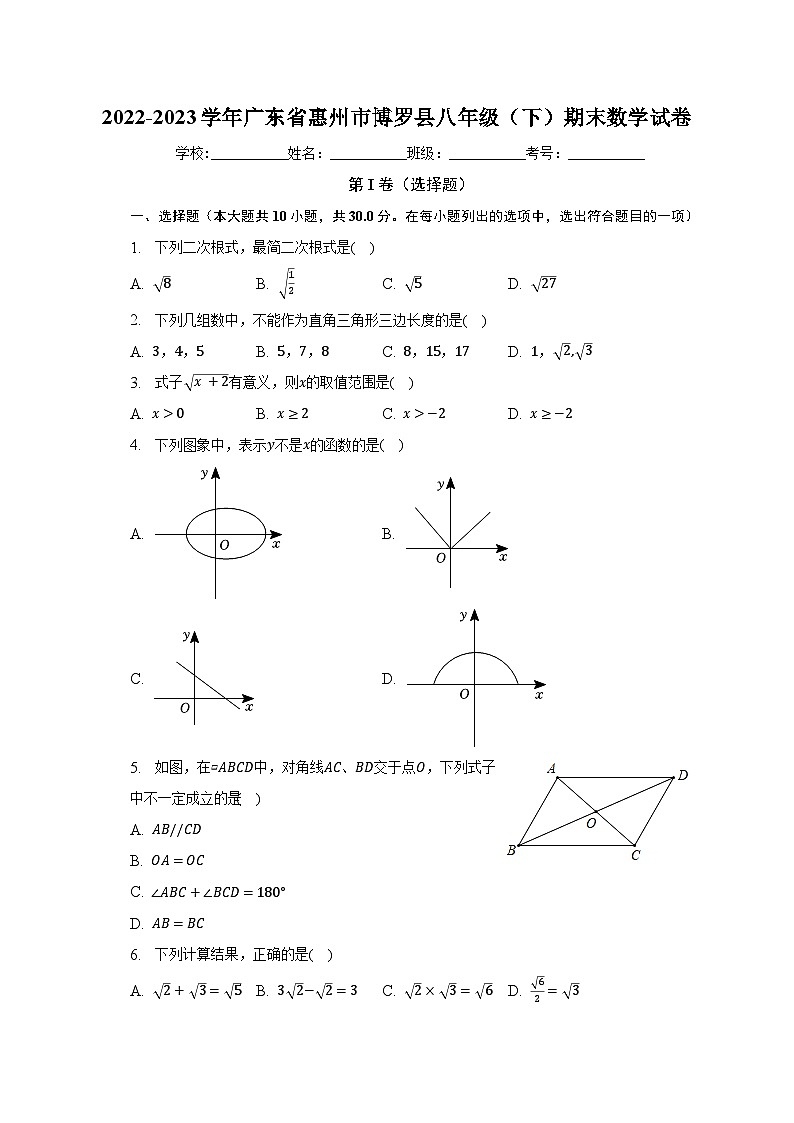
2022-2023学年广东省惠州市博罗县八年级（下）期末数学试卷
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列二次根式，最简二次根式是(    )
A. 8 B. 12 C. 5 D. 27
2. 下列几组数中，不能作为直角三角形三边长度的是(    )
A. 3，4，5 B. 5，7，8 C. 8，15，17 D. 1， 2, 3
3. 式子 x+2有意义，则x的取值范围是(    )
A. x>0 B. x≥2 C. x>−2 D. x≥−2
4. 下列图象中，表示y不是x的函数的是(    )
A. B.
C. D.
5. 如图，在▱ABCD中，对角线AC、BD交于点O，下列式子中不一定成立的是(    )
A. AB//CD
B. OA=OC
C. ∠ABC+∠BCD=180°
D. AB=BC
6. 下列计算结果，正确的是(    )
A. 2+ 3= 5 B. 3 2− 2=3 C. 2× 3= 6 D. 62= 3
7. 如图，在▱ABCD中，对角线AC、BD相交于点O，且OA=OB，若AD=4，∠AOD=60°，则AB的长为(    )


A. 4 3 B. 2 3 C. 8 D. 8 3
8. 一组数据3、2、4、5、2，则这组数据的众数是(    )
A. 2 B. 3 C. 3.2 D. 4
9. 对于函数y=−3x+4，下列结论正确的是(    )
A. 它的图象必经过点(−1,1) B. 它的图象不经过第三象限
C. 当x>0时，y>0 D. y的值随x值的增大而增大
10. 如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到(    )

A. M处 B. N处 C. P处 D. Q处
第II卷（非选择题）
二、填空题（本大题共5小题，共15.0分）
11. 菱形的对角线长分别为6和8，则该菱形的面积是______ ．
12. 甲、乙两个样本，甲的方差为0.102，乙的方差为0.06，哪个样本的数据波动大？答：______．
13. 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为PQ，则线段BQ的长度为______ ．


14. 实数a、b在数轴上位置如图，化简：|a+b|+ (a−b)2=______．
15. 如图，正方形ABCD的边长为2，顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1，再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…，以此类推，则第五个正方形A5B5C5D5周长是______ ．

三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题8.0分)
计算： 2× 6+ (−2)2−6 3．
17. (本小题8.0分)
已知y与x成正比例，且x=2时，y=−6.求：y与x的函数解析式．
18. (本小题8.0分)
如图四边形ABCD是一块草坪，量得四边长AB=3m，BC=4m，DC=12m，AD=13m，∠B=90°，求这块草坪的面积．

19. (本小题9.0分)
珠海市某中学在创建“书香校园”活动中，为了解学生的读书情况，某校抽样调查了部分同学在一周内的阅读时间，绘制如下统计图．根据图中信息，解答下列问题：
(1)被抽查学生阅读时间的中位数为______h，平均数为______h；
(2)若该校共有1500名学生，请你估算该校一周内阅读时间不少于3h的学生人数．

20. (本小题9.0分)
如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边中点，它的顶端恰好到达池边的水面，求这根芦苇的长度是多少尺？

21. (本小题9.0分)
如图，已知DB//AC，E是AC的中点，DB=AE，连结AD、BE．
(1)求证：四边形DBCE是平行四边形；
(2)若要使四边形ADBE是矩形，则△ABC应满足什么条件？说明你的理由．


22. (本小题12.0分)
如图，已知函数y=mx+43的图象为直线l1，函数y=kx+b的图象为直线l2，直线l1、l2分别交x轴于点B和点C(3,0)，分别交y轴于点D和E，l1和l2相交于点A(2,2)．
(1)填空：m=______；求直线l2的解析式为______；
(2)若点M是x轴上一点，连接AM，当△ABM的面积是△ACM面积的2倍时，请求出符合条件的点M的坐标；
(3)若函数y=nx−6的图象是直线l3，且l1、l2、l3不能围成三角形，直接写出n的值．

23. (本小题12.0分)
如图，矩形ABCD的对角线AC，BD相交于点O，将△COD沿CD所在直线折叠，得到△CED．
(1)求证：四边形OCED是菱形；
(2)若AB=2，当四边形OCED是正方形时，求OC的长；
(3)若BD=3，∠ACD=30°，P是CD边上的动点，Q是CE边上的动点，求PE+PQ的最小值．


答案和解析

1.【答案】C 
【解析】解：A、被开方数含开的尽的因数，故A不符合题意；
B、被开方数含分母，故B不符合题意；
C、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故C符合题意；
D、被开方数含能开得尽方的因数或因式，故D不符合题意；
故选：C．
检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．
本题考查最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．

2.【答案】B 
【解析】解：A、32+42=52，符合勾股定理的逆定理，能作为直角三角形三边长度；
B、52+72≠82，不符合勾股定理的逆定理，不能作为直角三角形三边长度；
C、82+152=172，符合勾股定理的逆定理，能作为直角三角形三边长度；
D、12+( 2)2=( 3)2，符合勾股定理的逆定理，能作为直角三角形三边长度．
故选：B．
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个三角形就不是直角三角形．
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．

3.【答案】D 
【解析】解：式子 x+2有意义，则x+2≥0，
解得：x≥−2．
故选：D．
根据二次根式中的被开方数是非负数，即可得出答案．
此题主要考查了二次根式有意义的条件，正确把握二次根式有意义的条件是解题关键．

4.【答案】A 
【解析】解：由函数的定义：设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，
选项A中的图象，y不是x的函数，故A符合题意；
选项B、C、D中的图象，y是x的函数，故B、C、D不符合题意．
故选：A．
设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，由此即可判断．
本题考查函数的概念，关键是掌握函数的定义．

5.【答案】D 
【解析】解：∵四边形ABCD是平行四边形，
∴AB//CD，AB=CD，AD=BC，AO=CO，BO=DO，∠ABC+∠BCD=180°，
故A、B、C都成立，只有D不一定成立，
故选：D．
根据平行四边形的性质对各个选项进行分析，进而选择正确的答案即可．
本题主要考查了平行四边形的性质，熟练掌握平行四边形的性质是解决问题的关键．

6.【答案】C 
【解析】解：A、 2与 3不能合并，所以A选项错误；
B、原式=2 2，所以B选项错误；
C、原式= 2×3= 6，所以C选项正确；
D、 62为最简二次根式，所以D选项错误．
故选：C．
根据二次根式的加减法对A、B进行判断；根据二次根式的乘法法则对C进行判断；根据最简二次根式的定义对D进行判断．
本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后合并同类二次根式即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．

7.【答案】A 
【解析】解：∵四边形ABCD为平行四边形，
∴OD=OB．
∵OA=OB，
∴OA=OD．
又∵∠AOD=60°，
∴△AOD为的等边三角形．
∴∠ADB=60°．
∴tan∠ADB=ABAD= 3．
∴AB= 3AD=4 3．
故选：A．
先证明OD=OA，于是可证明△AOD为等边三角形，最后在△DAB中，依据特殊锐角三角函数值可求得AB的长．
本题主要考查的是平行四边形的性质、等边三角形的判定、特殊锐角三角函数值的应用，求得∠ADB=60°是解题的关键．

8.【答案】A 
【解析】
【分析】
根据众数的定义即可求出这组数据的众数．
此题考查了众数的定义：众数是一组数据中出现次数最多的数据．
【解答】
解：在这组数据中2出现了2次，出现的次数最多，则这组数据的众数是2，
故选：A．  
9.【答案】B 
【解析】
【分析】
此题主要考查了一次函数图象上点的坐标特点，以及一次函数的性质，关键是掌握k>0，y随x的增大而增大，函数从左到右上升；k