2022-2023学年河南省商丘市虞城县部分学校八年级（下）期末数学试卷（B卷）（含解析）

这是一份2022-2023学年河南省商丘市虞城县部分学校八年级（下）期末数学试卷（B卷）（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年河南省商丘市虞城县部分学校八年级（下）期末数学试卷（B卷）
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列各式是最简二次根式的是(    )
A. 0.1 B. 12 C. 8 D. 3
2. 下列计算正确的是(    )
A. 2+ 3= 5 B. 2⋅ 3= 5 C. a2⋅a3=a5 D. 23=32
3. 下列各组线段中，不能够组成直角三角形的是(    )
A. 1，1， 2 B. 1， 2， 3 C. 1，2， 3 D. 1，2，3
4. 若y关于x的函数y=(m−1)x+n是正比例函数，则m，n应满足的条件是(    )
A. m≠1且n≠0 B. m=1且n≠0 C. m=1且n=0 D. m≠1且n=0
5. 如图，为测量池塘两端A，B的距离，可先在平地上取一个点O，从点O不经过池塘可以直接到达点A和B，连接OA，OB，分别取OA，OB的中点C，D，连接CD后，量出CD的长为10米，那么就可以算出A，B的距离是(    )


A. 12米 B. 16米 C. 20米 D. 24米
6. 积沙成塔，爱心昭昭.某校初中部教职工为病患学生捐款分布情况如下表所示，对于不同的x，下列关于捐款金额的统计量不会发生改变的是(    )
捐款金额/元
100
120
150
200
频数/人
5
15
x
10−x

A. 众数、中位数 B. 平均数、中位数 C. 平均数、方差 D. 中位数、方差
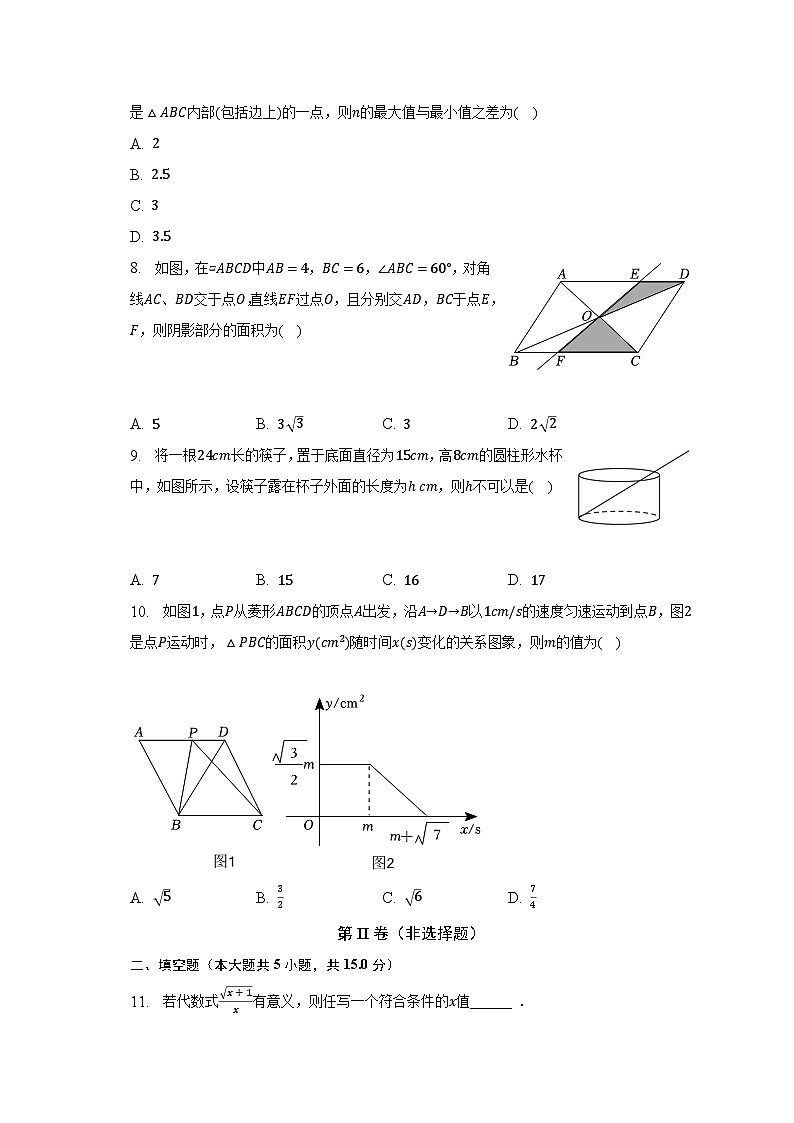
7. 如图，直线y1=x+2分别与x轴、y轴交于点A和点B，直线y2=−x+2分别与x轴、y轴交于点C和点B，点P(n,12)是△ABC内部(包括边上)的一点，则n的最大值与最小值之差为(    )
A. 2
B. 2.5
C. 3
D. 3.5
8. 如图，在▱ABCD中AB=4，BC=6，∠ABC=60°，对角线AC、BD交于点O，直线EF过点O，且分别交AD，BC于点E，F，则阴影部分的面积为(    )


A. 5 B. 3 3 C. 3 D. 2 2
9. 将一根24cm长的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为h cm，则h不可以是(    )


A. 7 B. 15 C. 16 D. 17
10. 如图1，点P从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，图2是点P运动时，△PBC的面积y(cm2)随时间x(s)变化的关系图象，则m的值为(    )


A. 5 B. 32 C. 6 D. 74
第II卷（非选择题）
二、填空题（本大题共5小题，共15.0分）
11. 若代数式 x+1x有意义，则任写一个符合条件的x值______ ．
12. 直角三角形的两条直角边长分别为3和4，则这个直角三角形斜边上的高为______ ．
13. 2023年春季开学伊始，流感在全国多个区域频发.某中学为有效预防流感，购买了A，B，C，D四种艾条进行消毒，它们的单价分别是30元，24元，20元，16元.四种艾条的购买比例如图所示，那么所购买艾条的平均单价是______ ．


14. 已知方程组y=kx−by=−x+a的解为x=−1y=2，则函数y=kx−b−2与函数y=−x+a−2的图象交点坐标为______ ．
15. 如图，在矩形纸片ABCD中，AD=2 2，AB=2，点P是AB的中点，点Q是BC边上的一个动点，将△PBQ沿PQ所在直线翻折，得到△PEQ，连接DE，CE，则当△DEC是以DE为腰的等腰三角形时，BQ的长是______ ．
三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题10.0分)
(1)计算： 8− 3× 6+(2023−π)0．
(2)一次函数y=(a−1)x+a+1(a为常数)的图象如图所示，求a的取值范围．

17. (本小题9.0分)
2023年3月30日，“中原一号”“鹤壁一、二、三号”4颗卫星发射升空.从河南籍航天员陈冬、刘洋出征太空，到河南首颗卫星“河南一号”发射升空，再到如今四颗“河南星”成功发射…越来越多的“河南造”挺起了我国航天事业，我大河南“真中”!洛阳某校组织了关于航天知识的竞赛活动，为了解学生对相关知识掌握的整体情况，分别从七、八年级各随机抽取20名学生的竞赛成绩(满分：100分)进行整理、描述和分析，给出以下部分信息：
Ⅰ.七年级20名学生竞赛成绩的频数分布表和频数分布直方图如图：
七年级20名学生竞赛成绩的频数分布表
成绩m/分
频数(人数)
50≤m<60
a
60≤m<70
b
70≤m<80
3
80≤m<90
8
90≤m≤100
6
合计
20
Ⅱ.七年级竞赛成绩在80≤m<90组的具体成绩为：83，84，86，87，88，89，89，89．
Ⅲ.七、八年级竞赛成绩的统计数据如右表所示：
年级
平均分
中位数
众数
七年级
83.7
n
89
八年级
84.2
85
85
年级根据以上信息，解答下列问题：
(1)a= ______ ；n= ______ ；
(2)补全七年级20名学生竞赛成绩的频数分布直方图；
(3)在这次竞赛活动中，某学生的竞赛成绩是86分，在他所属的样本中位于中等偏上水平，那么这个学生是______ 年级的学生，请说明理由．

18. (本小题9.0分)
下面是某同学学习完“特殊的平行四边形”后对某一道试题的证明：
试题：如图，在平行四边形ABCD中，对角线AC的垂直平分线EF交AD于点F，交BC于点E，交AC于点O.求证：四边形AECF是菱形．
证明：∵EF是AC的垂直平分线，
∴OA=OC，…①
OE=OF，…②
∴四边形AECF是平行四边形.…③
∵EF⊥AC…④
∴平行四边形AECF是菱形…⑤
(1)该同学的证明过程在第______ 步出现了错误；
(2)按照该同学的证明过程，步骤③的依据是______ ；步骤⑤的依据是______ ；
(3)写出此题的正确解答过程．

19. (本小题9.0分)
如图，在△ABC中，AD⊥BC，垂足为D，AD=4，BD=2，CD=8．
(1)求证：∠BAC=90°；
(2)请用圆规在BC边上求作点P，使BA=BP；(要求：不写作法，保留作图痕迹)
(3)在(2)的条件下，求PC的长．

20. (本小题9.0分)
2022年河南省全民健身(线上)运动会最终各奖项于12月20日公布，此次盛会充分展示疫情防控常态化下我省全民健身开展情况，某健身房于此推出“云健身”服务，针对特殊人群开展活动.活动方案如下：方案一：不购买“云VIP”，每次收费10元；方案二：购买“云VIP”，每次另行额外收费．
设王先生“云健身”次数为x(次)，按照方案一所需费用为y1(元)，且y1=kxx(k1≠0)；按照方案二所需费用为y2(元)，且y2=k2x+b(k2≠0).其函数图象如图所示．
(1)k1= ______ ；购买“云VIP”需______ 元；
(2)两种方案的函数图象交于点A，请求出点A的坐标并解释点A的实际意义；
(3)若王先生准备“云健身”25次，选择方案______ (选填“一”或“二”)所需费用较少；若王先生准备180元进行“云健身”，选择方案______ (选填“一”或“二”)可以获得更多的次数．

21. (本小题9.0分)
如图，直线AB分别与x轴、y轴交于点A、B，且点A的坐标为(4,0)，点B的坐标为(0,3)，在直线AB的右侧作正方形ABCD. (1)求直线AB的函数解析式；
(2)正方形ABCD的面积是______ ；
(3)求点C的坐标．

22. (本小题10.0分)
2023年是中国农历兔年，兔年春联、兔子玩偶、兔子饰品等商品占据周口批发市场“C位”，让市民忍不住“买买买”.某大学生选中如图所示的甲、乙两种玩偶，决定进货并销售.第一次该大学生购进了甲玩偶40个和乙玩偶12个共花费1500元，已知购进1个甲玩偶和1个乙玩偶共需55元，销售时每个甲玩偶可获利10元，每个乙玩偶可获利8元．
(1)求两种玩偶的进货单价分别是多少元？
(2)第二次进货时，该大学生计划购进两种玩偶共100个，且甲玩偶进货数量不得超过乙玩偶进货数量的2倍.他应如何设计进货方案才能获得最大利润，最大利润是多少元？

23. (本小题10.0分)
下面是平顶山某初中数学小组对某教材P198一道习题的探究，请仔细阅读，并完成任务．
“三等分一个任意角”是数学史上一个著名问题.今天人们已经知道，仅用圆规和直尺是不可能作出的.在探索中，有人曾利用过如图所示的图形，其中，ABCD是长方形，F是DA延长线上一点，G是F上一点，并且∠ACG=∠AGC，∠GAF=∠F.你能证明∠ECB=13∠ACB吗？
小明：经过分析，得出结论：点G是线段EF的中点，且EF=2AC；
小丽：你的结论正确，若把条件“G是CF上一点，并且∠ACG=∠AGC，∠GAF=∠F”去掉，并把你的结论当成已知条件，也能完成三等分角的证明，有异曲同工之妙．
任务一：请你根据小丽的思路，将下面的“已知”和“求证”补充完整，并写出“证明”过程．
已知：ABCD是矩形，F是DA延长线上一点，点G是EF的中点，且______ ；
求证：______ ；
证明：
任务二：如图，在矩形ABCD中，对角线AC的延长线与∠CBE的平分线交于点F，若BF=12AC，CF=4，求BF的长．




答案和解析

1.【答案】D 
【解析】解：A、 0.1= 110= 1010，故A不符合题意；
B、 12= 22，故B不符合题意；
C、 8=2 2，故C不符合题意；
D、 3是最简二次根式，故D符合题意；
故选：D．
根据最简二次根式的定义，即可解答．
本题考查了最简二次根式，熟练掌握最简二次根式的定义是解题的关键．

2.【答案】C 
【解析】解：A． 2与 3不是同类二次根式，无法合并，
则A不符合题意；
B. 2⋅ 3= 6，
则B不符合题意；
C.a2⋅a3=a2+3=a5，
则C符合题意；
D.23=8，32=9，8≠9，
则D不符合题意；
故选：C．
利用二次根式的运算法则，同底数幂乘法法则，有理数的乘方将各项计算后进行判断即可．
本题考查二次根式的运算，同底数幂乘法及有理数的乘方，其相关运算法则是基础且重要知识点，必须熟练掌握．

3.【答案】D 
【解析】解：A、∵12+12=( 2)2，∴能够组成直角三角形，故本选项不符合题意；
B、∵12+( 2)2=( 3)2，∴能够组成直角三角形，故本选项不符合题意；
C、∵12+( 3)2=22，∴能够组成直角三角形，故本选项不符合题意；
D、∵12+22≠32，∴不能够组成直角三角形，故本选项符合题意．
故选：D．
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．

4.【答案】D 
【解析】解：∵y关于x的函数y=(m−1)x+n是正比例函数，
∴m−1≠0，n=0．
解得m≠1，n=0．
故选：D．
根据正比例函数的定义列出：m−1≠0，n=0.据此可以求得m，n应满足的条件．
本题考查的是正比例函数的定义，即一般地，形如y=kx(k是常数，k≠0)的函数叫做正比例函数．

5.【答案】C 
【解析】解：∵C、D分别是OA、OB的中点，
∴CD是△AOB的中位线，
∴AB=2CD=20(米)．
故选：C．
由D，C分别是边OB，OA的中点，首先判定DC是三角形AOB的中位线，然后根据三角形的中位线定理，由CD的长，进一步求出AB．
此题是中位线定理，中位线是三角形中的一条重要线段，由于它的性质与线段的中点及平行线紧密相连，因此，它在几何图形的计算及证明中有着广泛的应用．

6.【答案】A 
【解析】解：由题意知捐款150元和捐款200元的人数和为x+10−x=10，
∴这组数据的众数为120，中位数是120+1202=120，
∴捐款金额的统计量不会发生改变的是众数和中位数，
故选：A．
由题意知捐款150元和捐款200元的人数和，继而依据众数和中位数的定义求解即可．
本题主要考查方差，解题的关键是掌握方差、中位数、众数及平均数的定义．

7.【答案】C 
【解析】解：∵点P(n,12)是△ABC内部(包括边上)的一点，
∴当点P在直线y1=x+2上时，n取得最小值，当点P在直线y2=−x+2上时，取得最大值，
将y1=12代入y1=x+2可得x=−32；将y2=12代入y2=−x+2可得x=32；
∴n的最大值与最小值之差为：32−(−32)=32+32=3，
故选：C．
根据题意和图象可知：当点P在直线y1=x+2上时，n取得最小值，当点P在直线y2=−x+2上时，取得最大值，然后计算出最大值和最小值作差即可．
本题考查一次函数的性质，解答本题的关键是明确题意，求出点P横坐标的最大值和最小值．

8.【答案】B 
【解析】解：在▱ABCD中，OB=OD，AD//BC，
∴∠EDO=∠FBO，
∵∠EOD=∠FOB，
∴△EOD≌△FOB(ASA)，
∴S△EOD=S△FOB，
如图，过点A作AG⊥BC于点G，
在▱ABCD中，AB=4，∠ABC=60°，
∴BF=12AB=2，
∴AF= 3BF=2 3，
∴▱ABCD的面积=BC⋅AF=6×2 3=12 3，
∴S阴影=S△EOD+S△COF=S△FOB+S△COF=S△BOC=14×▱ABCD的面积=14×12 3=3 3，
故选：B．
根据平行四边形的性质证明△EOD≌△FOB(ASA)，得S△EOD=S△FOB，过点A作AG⊥BC于点G，证明▱ABCD的面积=BC⋅AF=12 3，所以S阴影=S△EOD+S△COF=S△FOB+S△COF=S△BOC=14×▱ABCD的面积，进而可以解决问题．
此题主要考查了平行四边形的性质以及全等三角形的判定和性质，能够根据三角形全等，从而将阴影部分的面积转化为平行四边形面积的四分之一，是解决问题的关键．

9.【答案】D 
【解析】解：如图1所示，当筷子的底端在D点时，筷子露在杯子外面的长度最长，

∴h最大=24−8=16，
如图2所示，当筷子的底端在A点时，筷子露在杯子外面的长度最短，

在Rt△ABD中，AD=15cm，BD=8cm，
∴AB= AD2+BD2=17(cm)，
∴此时h最小=24−17=7，
∴h的取值范围是7≤h≤16．
故选：D．
如图，当筷子的底端在A点时，筷子露在杯子外面的长度最短；当筷子的底端在D点时，筷子露在杯子外面的长度最长．然后分别利用已知条件根据勾股定理即可求出h的取值范围．
本题主要考查了勾股定理的应用，明确题意，准确构造直角三角形是解题的关键．

10.【答案】D 
【解析】解：如图1，作DH⊥BC于H，
由图2得，当点P运动到点D时的时间为m s，即路程AD=m cm，
△PBC的面积y为 32m cm2，即12BC⋅DH= 32m，
∴DH= 3 cm，
当点P到达点B时用时(m+ 7)s，即AD+BD=(m+ 7) cm，
∴BD= 7 cm，
∴BH= BD2−DH2=2 cm，
在Rt△DHC中，HC2+DH2=CD2，即(m−2)2+( 3)2=m2，
∴m=74，
故选：D．

如图1，作DH⊥BC于H，由2得，当点P运动到点D时的时间为m s，即路程AD=m cm，根据△PBC的面积求出DH，再在Rt△DHC中利用勾股定理求出m即可．
本题考查了动点问题的函数图象，菱形性质及勾股定理的计算是解题关键．

11.【答案】2(答案不唯一) 
【解析】解：要使代数式 x+1x有意义，必须x+1≥0且x≠0，
解得：x≥−1且x≠0，
符合条件的x值为2．
故答案为：2(答案不唯一)．
根据二次根式有意义的条件和分式有意义的条件得出x+1≥0且x≠0，再求出答案即可．
本题考查了二次根式有意义的条件和分式有意义的条件，能熟记二次根式有意义的条件是解此题的关键，注意： a中a≥0．

12.【答案】125 
【解析】解：设直角三角形斜边上的高为h，
斜边长= 32+42=5，
则12×3×4=12×5×h，
解得：h=125，
故答案为：125．
根据勾股定理、三角形的面积公式计算，得到答案．
本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2.会用等面积法求直角三角形斜边上的高是解题的关键．

13.【答案】13.21元 
【解析】解：由图可得，所购买艾条的平均单价是：30×10%+24×25%+20×40%+16×25%=13.21(元)．
故答案为：13.21元．
根据题意中的数据和扇形统计图中的数据，可以计算出所购买艾条的平均单价．
本题考查加权平均数，解答本题的关键是明确加权平均数的计算方法．

14.【答案】(−1,0) 
【解析】解：∵方程组y=kx−by=−x+a的解为x=−1y=2，
∴函数y=kx−b−2与函数y=−x+a−2的图象交点坐标相对于函数y=kx−b与函数y=−x+a的图象交点(−1,2)向下平移2个单位长度为(−1,0)；
故答案为：(−1,0)．
根据一次函数与二元一次方程组的关系进行解答即可．
本题考查的是一次函数与二元一次方程组的关系，方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．

15.【答案】 2或1 
【解析】解：①当DE=DC时，如图1，连接DP，DQ，
∵点P是AB的中点，AB=2，AD=2 2，四边形ABCD是矩形，
∴∠A=90°，AP=PB=1，
∴DP= AD2+AP2= 8+1=3，
∵将△PBQ沿PQ所在直线翻折，得到△PEQ，
∴PE=PB=1，
∵DE=DC=AB=2，
∴PE+DE=1+2=3，
∴DP=3=PE+ED，
∴点P，E，D三点共线，
∵∠B=∠DCB=90°，
∴∠DEQ=∠DCQ=90°，
设BQ=x，则QE=x，CQ=2 2−x，
在Rt△DEQ和Rt△DCQ中，根据勾股定理得：DQ2=DE2+EQ2=DC2+CQ2，
∴22+x2=22+(2 2−x)2，
解得：x= 2，
∴BQ= 2；
②当DE=EC时，如图2，
∵DE=EC，
∴点E在线段CD的垂直平分线上，
∴点E在线段AB的垂直平分线上，
∵点P是AB的中点，
∴EP是AB的垂直平分线，
∴∠BPE=90°，
∵将△PBQ沿PQ所在直线翻折，得到△PEQ，
∴∠B=∠PEQ=90°，PB=PE，
∴四边形BPEQ是正方形，
∴BQ=PB=1，
综上所述：BQ的长为： 2或1．
故答案为： 2或1．
存在两种情况：当DE=DC，连接DP，DQ，勾股定理求得DP的长，可判断P，E，D三点共线，根据勾股定理即可得到结论；当DE=EC，证明BPEQ是正方形，可得到结论．
本题考查了翻折变换(折叠问题)，矩形的性质，等腰三角形的性质，正方形的判定和性质，分类讨论思想的运用是解题的关键．

16.【答案】解：(1)原式=2 2−3 2+1
=1− 2．
(2)由一次函数y=(a−1)x+a+1的图象得：a−1<0a+1<0，
∴由①得a<1，由②得a<−1．
∴a的取值范围为：a<−1． 
【解析】(1)依据题意，由实数的性质进行运算可以得解；
(2)依据题意，由一次函数的图象与性质可以判断：a−1<0，a+1<0，从而可以得解．
本题主要考查了实数的性质及一次函数的图象与性质，解题时要熟练掌握并灵活运用是关键．

17.【答案】1  87.5  八 
【解析】解：(1)由题意得：a=20×0.05=1；
把七年级20名学生的竞赛成绩从小到大排列，排在中间的两个数分别是87、88，故中位数m=87+882=87.5；
故答案为：1；87.5；
(2)由题意知，成绩在“60≤x<70”这一组的人数为2人，
将频数分布直方图补充完整如下：

(3)八年级．
理由：∵86>85，86<87.5，
∴该同学竞赛成绩高于八年级的中等水平，低于七年级的中等水平；
故答案为：八．
(1)根据“频率=频数÷总数”可得a的值，根据中位数的定义可得m的值；
(2)用20分别减去其它组的频数可得b的值，再补全频数分布直方图即可；
(3)根据中位数的意义解答即可．
本题考查频数分布直方图、频数分布表，中位数以及众数，理解中位数、众数的意义，掌握它们的计算方法是正确求解的前提．

18.【答案】②  对角线互相平分的四边形是平行四边形  对角线互相垂直的平行四边形是菱形 
【解析】解：(1)该同学的证明过程在第②步出现了错误；
故答案为：②；
(2)按照该同学的证明过程，步骤③的依据是对角线互相平分的四边形是平行四边形；步骤⑤的依据是对角线互相垂直的平行四边形是菱形；
故答案为：对角线互相平分的四边形是平行四边形；对角线互相垂直的平行四边形是菱形：
(3)证明：∵四边形ABCD是平行四边形，
∴AD/​/BC．
∴∠FAO=∠ECO，
∵EF是AC的垂直平分线，
∴EF⊥AC，OA=OC，
又∵∠AOF=∠COE，
∴△AOF≌△COE(ASA)，
∴EO=FO，
∴四边形AECF是平行四边形．
∵EF⊥AC．
∴平行四边形AECF是菱形．
(1)根据平行四边形的判定方法进行判断即可；
(2)根据平行四边形与菱形的判定方法进行解答；
(3)先根据平行四边形的性质得∠FAO=∠ECO，再由垂直平分线的性质得EF⊥AC，OA=OC，根据全等三角形的判定与性质及平行四边形的判定可得四边形AECF是平行四边形．最后由菱形的判定方法可得结论．
此题考查的是菱形的判定与性质、平行四边形的判定与性质，掌握其性质定理是解决此题的关键．

19.【答案】(1)证明：∵AD⊥BC，AD=4，BD=2，
∴AB2=AD2+BD2=20，
又∵AD⊥BC，CD=8，AD=4，
∴AC2=CD2+AD2=80，
∵BC=CD+BD=10，
∴BC2=100
∴AC2+AB2=100=BC2，
∴∠BAC=90°；
 (2)解：如图所示：
(3)解：∵AD⊥BC，
∴AB= BD2+AD2=2 5
∴BP=AB=2 5，
∴CP=BC−BP=10−2 5． 
【解析】(1)根据勾股定理的逆定理证明；
(2)根据作线段等于已知线段的基本做法作图；
(3)根据勾股定理求解．
本题考查了复杂作图，掌握勾股定理及勾股定理的逆定理是解题的关键．

20.【答案】10  120  二  一 
【解析】2解：(1)由题意得：y1=10x，由图象得：购买“云VIP”需120元，
故答案为：10，120；
(2)由题意得：y1=10x，
∵(0,120)(10,160)在y2=k2x+b上，
∴b=120160=10k2+b，
解得：k2=4b=120，
∴y2=4x+120，
令10x=4x+120，
解得x=20，
∴10x=200，
∴点A的坐标为(20,200)；
点A的实际意义为：当“云健身”20次时，两种方案所需费用相同，均为200元；
(3)由图象得：王先生准备“云健身”25次，选择方案二所需费用较少；
若王先生准备180元进行“云健身”，选择方案一可以获得更多的次数；
故答案为：二；一．
(1)分别根据题意和函数的图象求解；
(2)先根据待定系数法求出两个函数的解析式，再求出交点坐标，结合实际说出A点的意义；
(3)根据图象求解．
本题考查了一次函数的应用，掌握待定系数法和数形结合思想是解题的关键．

21.【答案】25 
【解析】解：(1)∵A(4,0)，B(0,3)，
∴OA=4，OB=3，
在Rt△AOB中，AB= AO2+BO2=5，
∴正方形ABCD面积=52=25，
故答案为：25；
(2)如图，过点C作CE⊥y轴于点E，

∵正方形ABCD中，∠ABC=90°，
∴∠CBE+∠ABO=90°，
∵∠ABO+∠BAO=90°，
∴∠CBE=∠BAO，
在△ABO和△BCE中，
∠BAO=∠CBE ∠BEC=∠AOB AB=BC ，
∴△ABO≌△BCE(AAS)，
∴CE=OB=3，BE=OA=4，
∴OE=4+3=7，
∴点C的坐标为(3,7)．
(1)利用勾股定理求出AB，即可得正方形ABCD面积；
(2)过点C作CE⊥y轴于点E，证明△ABO≌△BCE，即可得答案．
本题考查全等三角形的判定和性质，及勾股定理，掌握正方形的性质，是证明△ABO≌△BCE的关键．

22.【答案】解：(1)设每个甲玩偶的进价为x元，每个乙玩偶的进价为y元，
由题意可得：40x+12y=1500x+y=55，
解得x=30y=25，
答：每个甲玩偶的进价为30元，每个乙玩偶的进价为25元；
(2)设甲玩偶购进a个，则乙玩偶购进(100−a)个，利润为w元，
由题意可得：w=10a+8(100−a)=2a+800，
∴w随a的增大而增大，
∵甲玩偶进货数量不得超过乙玩偶进货数量的2倍，
∴a≤2(100−a)，
解得a≤1003，
∵a为整数，
∴当a=33时，w取得最大值，此时w=866，100−a=67，
答：甲玩偶购进33个，乙玩偶购进67个时才能获得最大利润，最大利润是866元． 
【解析】(1)设每个甲玩偶的进价为x元，每个乙玩偶的进价为y元，根据购进了甲玩偶40个和乙玩偶12个共花费1500元，购进1个甲玩偶和1个乙玩偶共需55元可以列出相应的二元一次方程组，然后求解即可；
(2)根据题意可以写出利润和甲玩偶数量的函数关系式，然后根据甲玩偶进货数量不得超过乙玩偶进货数量的2倍，可以求得甲玩偶数量的取值范围，再根据一次函数的性质，即可得到利润的最大值．
本题考查二元一次方程组的应用、一次函数的应用，解答本题的关键是明确题意，列出相应的方程组，写出相应的函数关系式，利用一次函数的性质求最值．

23.【答案】EF=2AC  ∠ECB=13∠ACB 
【解析】解：任务一：已知：EF=2AC，
求证：∠ECB=13∠ACB；
 证明：∵四边形ABCD是矩形，
∴∠DAB=90°，AD//BC，
∵点G是EF的中点，
∴AG=EG=GF，
∵EF=2AC，
∴AC=AG，
∴∠ACG=∠AGC，
∴∠ACG=∠ACC=∠F+∠GAF=2∠F，
∵AD/​/BC，
∴∠F=∠BCF，
∴∠ACG=2∠BCF，
∴∠ACB=3∠BCF，
∴∠ECB=13∠ACB；
故答案为：EF=2AC，∠ECB=13∠ACB；
任务二：取AC的中点H，连接BH，过点C作CG⊥BF于点G，

∵四边形ABCD是矩形，
∴∠ABC=90°，
∵点H是AC的中点，
∴AH=CH=BH，
∴∠HAB=∠HBA，
设∠HAB=∠HBA=x，
∴∠BHF=2x，
∵BF=12AC，
∴BH=BF，
∴∠F=∠BHF=2x，
∵∠CBE=90°，BF平分∠CBE，
∴∠FBE=∠CBF=45°，
∵∠FBE=∠HAB+∠F，
∴x+2x=45°，
∴x=15°，
∴∠F=30°，
∵CG⊥BF，CF=4，
∴CG=2，
∴FG= CF2−CG2= 42−22=2 3，
∵∠CBF=45°=∠BCG=45°，
∴CG=BG=2，
∴BF=BG+FG=2+2 3．
任务一：根据矩形的性质得到∠DAB=90°，AD//BC，根据直角三角形的性质得到AG=EG=GF，根据平行四边形的性质得到∠F=∠BCF，于是得到∠ECB=13∠ACB；
任务二：取AC的中点H，连接BH，过点C作CG⊥BF于点G，根据矩形的性质得到∠ABC=90°，根据直角三角形的性质得到AH=CH=BH，设∠HAB=∠HBA=x，得到∠BHF=2x，根据角平分线的定义得到∠FBE=∠CBF=45°，求得∠F=30°，根据勾股定理即可得到结论．
本题是四边形的综合题，考查了全等三角形 的判定和性质，矩形的性质，直角三角形的性质，勾股定理，正确地作出辅助线是解题的关键．