适用于新教材2024版高考数学一轮总复习第八章立体几何与空间向量第三节空间直线平面平行的判定与性质课件北师大版

这是一份适用于新教材2024版高考数学一轮总复习第八章立体几何与空间向量第三节空间直线平面平行的判定与性质课件北师大版，共44页。PPT课件主要包含了内容索引，强基础固本增分，研考点精准突破等内容，欢迎下载使用。

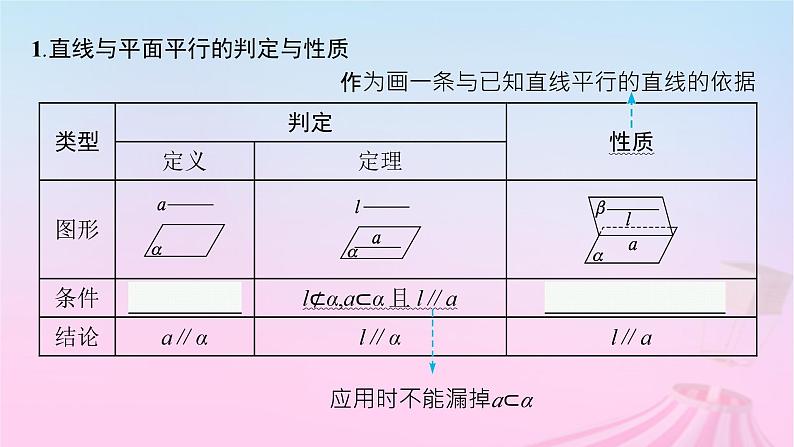
1.直线与平面平行的判定与性质
作为画一条与已知直线平行的直线的依据
　应用时不能漏掉a⊂α
微点拨 在推证线面平行时,一定要强调直线a不在平面内,直线b在平面内,且a∥b,否则会出现错误. 微思考 一条直线与一个平面平行,那么它与平面内的所有直线都平行吗?提示 不都平行.该平面内的直线有两类:一类与该直线平行,一类与该直线异面.
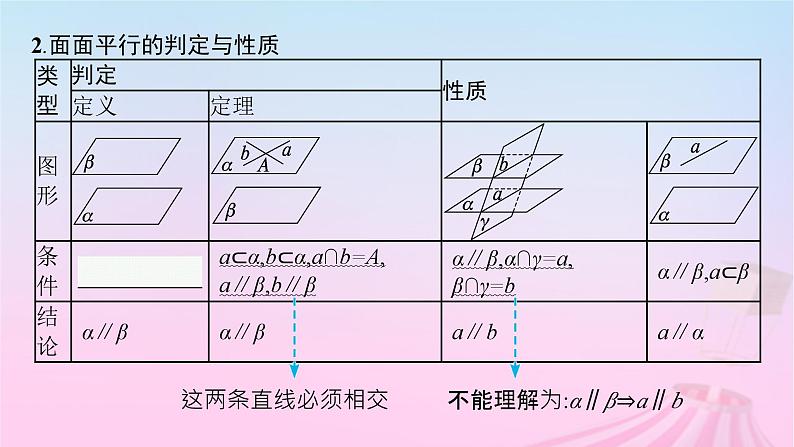
2.面面平行的判定与性质
　这两条直线必须相交　 不能理解为:α∥β⇒a∥b
微点拨 判定两个平面平行与判定线面平行一样,应遵循“先找后作”的原则,即先在一个平面内找到两条与另一个平面平行的相交直线,若找不到再作辅助线. 微思考 一个平面内的两条相交直线与另一个平面内的两条相交直线分别对应平行,那么这两个平面平行吗?提示 平行.可以转化为“一个平面内的两条相交直线与另一个平面平行”,这就是面面平行的判定定理.
常用结论1.平面与平面平行的三个性质(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两个平行平面间的平行线段长度相等.(3)两条直线被三个平行平面所截,截得的对应线段成比例.2.判断两个平面平行的三个结论(1)垂直于同一条直线的两个平面平行.(2)平行于同一平面的两个平面平行.(3)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.
自主诊断题组一　思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.(　　)2.若直线a与平面α内无数条直线平行,则a∥α.(　　)3.如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.(　　)4.如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.(　　)
题组二　双基自测5. 如果直线a∥平面α,P∈α,那么过点P且平行于直线a的直线(　　)A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内答案 C解析 根据直线与平面平行的性质定理,可知该直线为点P和直线a所确定的平面与平面α的交线,故该直线在平面α内有且只有一条.
6. 如图,在四面体D-ABC中, E,F,G分别是AB,BC,CD的中点,求证:(1)BD∥平面EFG;(2)AC∥平面EFG.
证明 (1)∵F,G分别是BC,CD的中点,∴FG∥BD.∵BD⊄平面EFG,FG⊂平面EFG,∴BD∥平面EFG.(2)∵E,F分别是AB,BC的中点,∴EF∥AC.∵AC⊄平面EFG,EF⊂平面EFG,∴AC∥平面EFG.
考向1直线与平面平行的判定例题 如图,在四棱锥E-ABCD中,AB∥CD,∠ABC=90°,CD=2AB=2CE=4,点F为棱DE的中点.证明:AF∥平面BCE.
证明 (方法1)如图,取CE的中点M,连接FM,BM.因为点F为棱DE的中点,所以FM∥CD,且FM= CD=2.因为AB∥CD,且AB=2,所以FM∥AB,且FM=AB,所以四边形ABMF为平行四边形,所以AF∥BM.因为AF⊄平面BCE,BM⊂平面BCE,所以AF∥平面BCE.
(方法2)如图,在平面ABCD内,分别延长CB,DA,交于点N,连接EN.因为AB∥CD,CD=2AB,所以A为DN的中点.又F为DE的中点,所以AF∥EN.因为EN⊂平面BCE,AF⊄平面BCE,所以AF∥平面BCE.
(方法3)如图,取棱CD的中点G,连接AG,GF,因为点F为棱DE的中点,所以FG∥CE.因为FG⊄平面BCE,CE⊂平面BCE,所以FG∥平面BCE.因为AB∥CD,AB=CG=2,所以四边形ABCG是平行四边形,所以AG∥BC.因为AG⊄平面BCE,BC⊂平面BCE,所以AG∥平面BCE.又FG∩AG=G,FG⊂平面AFG,AG⊂平面AFG,所以平面AFG∥平面BCE.因为AF⊂平面AFG,所以AF∥平面BCE.
规律方法 证明线面平行的两种常用方法
对点训练如图,在四棱锥P-ABCD中,AD∥BC,AB=BC= AD,E,F,H分别是线段AD,PC,CD的中点,AC与BE交于点O,G是线段OF上一点.求证:(1)AP∥平面BEF;(2)GH∥平面PAD.
证明 (1)连接EC,∵AD∥BC,BC= AD,E是AD的中点,∴BC AE,∴四边形ABCE是平行四边形,∴O为AC的中点.又F是PC的中点,∴FO∥AP.∵FO⊂平面BEF,AP⊄平面BEF,∴AP∥平面BEF.
(2)连接FH,OH,∵F,H分别是PC,CD的中点,∴FH∥PD.∵PD⊂平面PAD,FH⊄平面PAD,∴FH∥平面PAD.又O是AC的中点,H是CD的中点,∴OH∥AD.又AD⊂平面PAD,OH⊄平面PAD,∴OH∥平面PAD.又FH∩OH=H,FH,OH⊂平面OFH,∴平面OHF∥平面PAD.又GH⊂平面OHF,∴GH∥平面PAD.
考向2直线与平面平行的性质例题如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,O,M分别为BD,PC的中点.设平面PAD与平面PBC的交线为l.(1)求证:OM∥平面PAD.(2)求证:BC∥l.(3)在棱PC上是否存在点N(异于点C),使得BN∥平面PAD?若存在,求出 的值;若不存在,说明理由.
(1)证明 连接AC,因为底面ABCD为平行四边形,O为BD的中点,所以O为AC的中点.因为M为PC的中点,所以在△APC中,AP∥OM.因为OM⊄平面PAD,AP⊂平面PAD,所以OM∥平面PAD.(2)证明 因为底面ABCD为平行四边形,所以AD∥BC.因为AD⊂平面PAD,BC⊄平面PAD,所以BC∥平面PAD.因为平面PAD与平面PBC的交线为l,BC⊂平面PBC,所以BC∥l.
(3)解 不存在.理由如下,假设在棱PC上存在点N(异于点C),使得BN∥平面PAD.在平面PDC中,过点N作PD的平行线EN,交DC于点E.因为EN⊄平面PAD,PD⊂平面PAD,所以EN∥平面PAD.因为EN∩BN=N,所以平面BEN∥平面PAD.因为BE⊂平面BEN,所以BE∥平面PAD.又因为BE⊂平面ABCD,平面ABCD∩平面PAD=AD,所以BE∥AD.另一方面,在平行四边形ABCD中,BE与AD不平行,矛盾,所以在棱PC上不存在点N(异于点C),使得BN∥平面PAD.
规律方法 应用线面平行性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面来确定交线.
对点训练在空间四边形ABDC中,AD=BC=a,与直线AD,BC都平行的平面分别交AB,AC,CD,BD于点E,F,G,H.(1)求证:四边形EFGH是平行四边形;(2)求四边形EFGH的周长.
(1)证明 因为直线AD∥平面EFGH,AD⊂平面ABD,平面ABD∩平面EFGH=EH,所以AD∥EH.同理得AD∥FG,所以EH∥FG.同理得EF∥HG,所以四边形EFGH是平行四边形.
例题如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.
证明 (1)∵G,H分别是A1B1,A1C1的中点,∴GH是△A1B1C1的中位线,∴GH∥B1C1.又B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.(2)∵E,F分别是AB,AC的中点,∴EF∥BC.∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1∥AB且A1B1=AB,∴A1G∥EB,A1G=EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.又A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又A1E∩EF=E,A1E,EF⊂平面EFA1,∴平面EFA1∥平面BCHG.
引申探究1(变条件变结论)在本例中,若将条件“E,F,G,H分别是AB,AC, A1B1,A1C1的中点”变为“D1,D分别为B1C1,BC的中点”,求证:平面A1BD1∥平面AC1D.
证明 如图所示,连接A1C,AC1,交于点M.∵四边形A1ACC1是平行四边形,∴M是A1C的中点.连接MD,∵D为BC的中点,∴A1B∥DM.∵A1B⊂平面A1BD1,DM⊄平面A1BD1,∴DM∥平面A1BD1.又由三棱柱的性质知,D1C1∥BD且D1C1=BD,∴四边形BDC1D1为平行四边形,∴DC1∥BD1.又DC1⊄平面A1BD1,BD1⊂平面A1BD1,∴DC1∥平面A1BD1,又DC1∩DM=D,DC1,DM⊂平面AC1D,∴平面A1BD1∥平面AC1D.
引申探究2(变条件变结论)在本例中,若将条件“E,F,G,H分别是AB,AC, A1B1,A1C1的中点”变为“D,D1分别是棱AC,A1C1上的点,且平面BC1D∥平面AB1D1”,试求 的值.
解 连接A1B,AB1,交于点O,连接OD1.由平面BC1D∥平面AB1D1,且平面A1BC1∩平面BC1D=BC1,平面A1BC1∩平面AB1D1=D1O,所以BC1∥D1O,所以D1为A1C1的中点.同理,AD1∥C1D.又AD∥C1D1,所以四边形ADC1D1是平行四边形,所以AD=D1C1= A1C1.又AC=A1C1,所以AD= AC,
规律方法 证明面面平行的三种常用方法
对点训练如图,在三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,A1B1,AB的中点.(1)求证:平面A1C1G∥平面BEF;(2)若平面A1C1G∩BC=H,求证:H为BC的中点.
证明 (1)∵E,F分别为B1C1,A1B1的中点,∴EF∥A1C1.∵A1C1⊂平面A1C1G,EF⊄平面A1C1G,∴EF∥平面A1C1G.又F,G分别为A1B1,AB的中点,∴A1F=BG.又A1F∥BG,∴四边形A1GBF为平行四边形,则BF∥A1G.∵A1G⊂平面A1C1G,BF⊄平面A1C1G,∴BF∥平面A1C1G.又EF∩BF=F,EF,BF⊂平面BEF,∴平面A1C1G∥平面BEF.
(2)∵平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,平面A1C1G与平面ABC有公共点G,平面A1C1G∩BC=H,∴A1C1∥GH,得GH∥AC.∵G为AB的中点,∴H为BC的中点.
例题在直角梯形ABCD中(如图1),AB∥DC,∠BAD=90°,AB=5,AD=2, CD=3,点E在CD上,且DE=2,将△ADE沿AE折起,使得平面ADE⊥平面ABCE(如图2),G为AE的中点.
(1)求四棱锥D-ABCE的体积.(2)在线段BD上是否存在点P,使得CP∥平面ADE?若存在,求 的值;若不存在,请说明理由.
解 (1)因为G为AE的中点,AD=DE=2,所以DG⊥AE.因为平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,DG⊂平面ADE,所以DG⊥平面ABCE.
(2)在BD上存在点P,使得CP∥平面ADE.过点C作CF∥AE交AB于点F,过点F作FP∥AD交DB于点P,连接PC,如图所示.因为CF∥AE,AE⊂平面ADE,CF⊄平面ADE,所以CF∥平面ADE.同理,FP∥平面ADE.又因为CF∩PF=F,所以平面CFP∥平面ADE.因为CP⊂平面CFP,所以CP∥平面ADE.所以在BD上存在点P,使得CP∥平面ADE.因为四边形AECF为平行四边形,
规律方法 解决存在性问题的步骤
对点训练(2023·甘肃武威高三检测)如图,在三棱柱ABC-A1B1C1中,E,F分别为线段AC1,A1C1的中点.(1)求证:EF∥平面BCC1B1.(2)在线段BC1上是否存在一点G,使平面EFG∥平面ABB1A1?请说明理由.