适用于新教材2024版高考数学一轮总复习第八章立体几何与空间向量解答题专项四第3课时翻折问题与探索性问题课件北师大版

这是一份适用于新教材2024版高考数学一轮总复习第八章立体几何与空间向量解答题专项四第3课时翻折问题与探索性问题课件北师大版，共29页。PPT课件主要包含了规范解答等内容，欢迎下载使用。

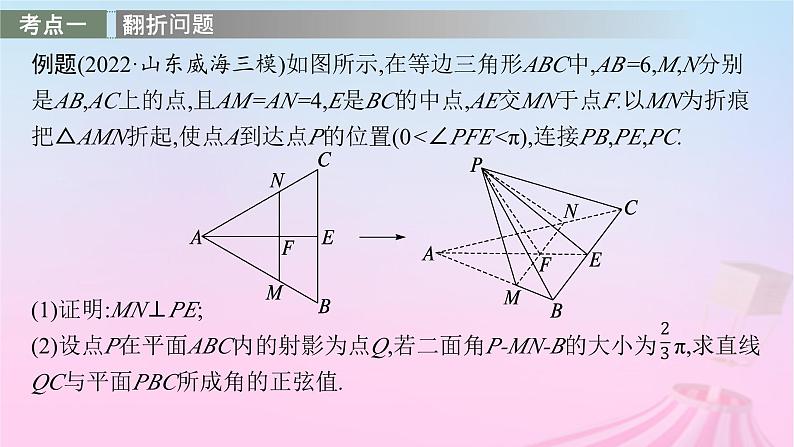
例题(2022·山东威海三模)如图所示,在等边三角形ABC中,AB=6,M,N分别是AB,AC上的点,且AM=AN=4,E是BC的中点,AE交MN于点F.以MN为折痕把△AMN折起,使点A到达点P的位置(0<∠PFE<π),连接PB,PE,PC.
(1)证明:MN⊥PE;(2)设点P在平面ABC内的射影为点Q,若二面角P-MN-B的大小为 π,求直线QC与平面PBC所成角的正弦值.
(1)证明 因为△ABC是等边三角形,E是BC的中点,所以AE⊥BC.因为AM=AN=4,所以MN∥BC,所以MN⊥AE,可得MN⊥PF,MN⊥EF,又PF∩FE=F,所以MN⊥平面PEF,又PE⊂平面PFE,所以MN⊥PE.(2)解 因为MN⊥PF,MN⊥FE,由第(1)问知,MN⊥平面PFE,MN⊂平面ABC,所以平面ABC⊥平面PFE,又因为平面PFE∩平面ABC=AE,所以点P在平面ABC内的射影点Q在AE上,
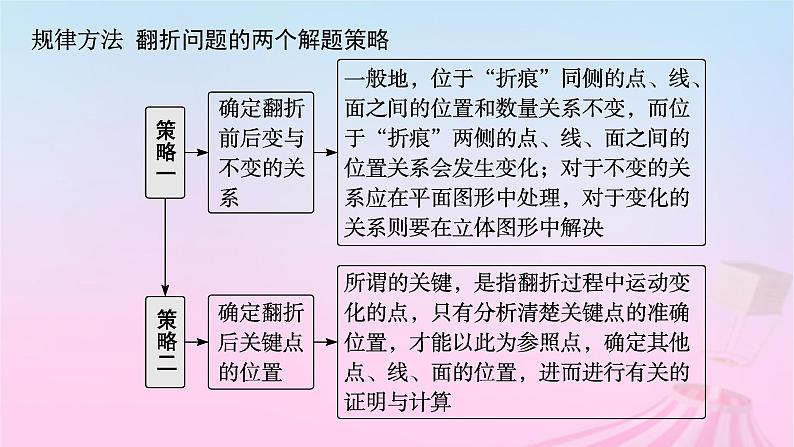
规律方法 翻折问题的两个解题策略
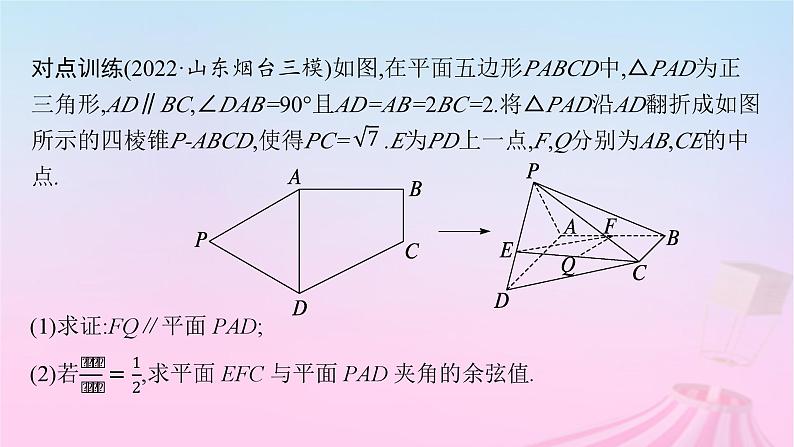
对点训练(2022·山东烟台三模)如图,在平面五边形PABCD中,△PAD为正三角形,AD∥BC,∠DAB=90°且AD=AB=2BC=2.将△PAD沿AD翻折成如图所示的四棱锥P-ABCD,使得PC= .E为PD上一点,F,Q分别为AB,CE的中点.
(1)证明 取DC的中点M,连接MF,MQ.则MQ∥PD,MF∥DA.因为MQ⊄平面PAD,MF⊄平面PAD,所以MQ∥平面PAD,MF∥平面PAD,MQ∩MF=M,所以平面MQF∥平面PAD,因为FQ⊂平面MQF,所以FQ∥平面PAD.
例题(2022·山东德州二模)《九章算术》是《算经十书》中最重要的一部,是当时世界上最简练有效的应用数学之一,它的出现标志着中国古代数学形成了完整的体系.在《九章算术·商功》篇中提到“阳马”这一几何体,是指底面为矩形,有一条侧棱垂直于底面的四棱锥,现有如图所示“阳马”P-ABCD,底面为边长为2的正方形,侧棱PA⊥平面
ABCD,PA=2,E,F为边BC,CD上的点,点M为AD的中点.(1)若λ= ,证明:平面PBM⊥平面PAF;(2)是否存在实数λ,使二面角P-EF-A的大小为45°?如果不存在,请说明理由;如果存在,求此时直线BM与平面PEF所成角的正弦值.
解 (1)当λ= 时,点E,F分别为BC,CD边上的中点,连接AF与BM交于点G,在△ABM和△DAF中,AB=AD,AM=DF,∠BAM=∠ADF=90°,所以△ABM≌△DAF,于是∠ABM=∠FAD.而∠FAD+∠BAF=90°,所以∠ABM+∠BAF=90°,故∠AGB=90°,即BM⊥AF.又PA⊥平面ABCD,BM⊂平面ABCD,所以PA⊥BM.因为BM⊥PA,BM⊥AF,PA⊂平面PAF,AF⊂平面PAF,PA∩AF=A,所以BM⊥平面PAF.又因为BM⊂平面PBM,所以平面PBM⊥平面PAF.
(2)连接AC,交EF于点Q,连接PQ,记BD与AC交于点O,如图:
因为AC⊥BD,所以AC⊥EF,又PA⊥平面ABCD,EF⊂平面ABCD,故PA⊥EF,又PA∩AC=A,故EF⊥平面PAC,PQ⊂平面PAC,从而PQ⊥EF,所以∠AQP为二面角P-EF-A的平面角.由题意,∠AQP=45°,从而AQ=PA=2,
规律方法 与空间角有关的存在性问题的解题流程
(1)当EN∥平面MBD时,求λ的值;(2)试探究:随着λ值的变化,二面角B-MD-E的大小是否改变?如果改变,请说明理由;如果不改变,请求出二面角B-MD-E的正弦值大小.
解 (1)取MB的中点为P,连接DP,PN,因为MN=CN,MP=BP,所以NP∥BC.又DE∥BC,所以NP∥DE,即N,E,D,P四点共面,又EN∥平面BMD,EN⊂平面NEDP,平面NEDP∩平面MBD=DP,所以EN∥PD,即四边形NEDP为平行四边形,所以NP=DE,则DE= BC,即λ= .
(2)取DE的中点O,连接MO,因为平面MDE⊥平面DECB,平面MDE∩平面DECB=DE,且MO⊥DE,所以MO⊥平面DECB,如图建立空间直角坐标系,
例题(12分)(2021·全国甲,理19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.(1)证明:BF⊥DE;(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?
(2)解 ∵BF⊥A1B1,∴BF⊥AB,∴AF2=BF2+AB2=CF2+BC2+AB2=9.又AF2=FC2+AC2,∴AC2=8,则AB⊥BC.
如图,以B为原点,BC,BA,BB1为x轴、y轴、z轴建立空间直角坐标系,则B(0,0,0),C(2,0,0),A(0,2,0),E(1,1,0),F(2,0,1).设DB1=t,则D(0,t,2),0≤t≤2.
【教师讲评】 (1)本题第(1)问的解答为常规方法,借助题目条件,利用平面几何知识,通过证明全等得某个角为90°,则说明线线垂直,进而可证线面垂直,再由性质得线线垂直.(2)本例第(2)问先建立坐标系,设DB1=t,将相关点坐标表示出来,利用法向量夹角与二面角的关系,将所求最值转化为关于t的函数问题求最值.
规律方法 求最值、范围问题的常用思路
对点训练(12分)如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,△PAC为正三角形,E,F分别是PC,PB上的动点.(1)求证:BC⊥AE;(2)若E,F分别是PC,PB的中点且异面直线AF与BC所成角的正切值为 ,记平面AEF与平面ABC的交线为直线l,点Q为直线l上一动点,求直线PQ与平面AEF所成角的取值范围.
以C为坐标原点,CA,CB所在直线分别为x轴,y轴,过C且垂直于平面ABC的直线为z轴,建立如图所示空间直角坐标系,设AC=2.
因为△PAC为正三角形,所以AE= ,从而EF=2.