适用于新教材2024版高考数学一轮总复习第九章平面解析几何第五节椭圆课件北师大版

这是一份适用于新教材2024版高考数学一轮总复习第九章平面解析几何第五节椭圆课件北师大版，共46页。PPT课件主要包含了内容索引，强基础固本增分，研考点精准突破，答案B，答案BCD，考向2椭圆的离心率，答案C等内容，欢迎下载使用。
1.椭圆的定义平面内到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的集合(或轨迹)叫作椭圆.这两个定点F1,F2叫作椭圆的　焦点　,两焦点间的距离|F1F2|叫作椭圆的　焦距　. 微点拨 当2a=|F1F2|时,点M的轨迹是线段F1F2;当2a|F1F2|}
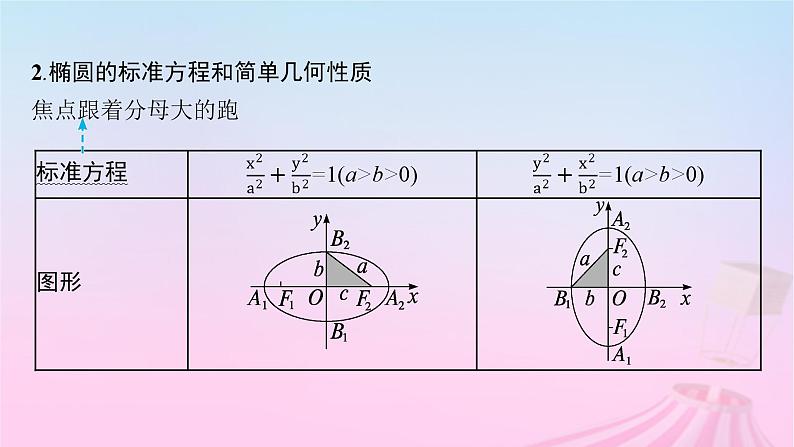
2.椭圆的标准方程和简单几何性质焦点跟着分母大的跑

微点拨 1.椭圆的焦点F1,F2必在它的长轴上.2.求椭圆离心率e时,只要得出a,b,c的一个方程,再结合b2=a2-c2就可求得e(00,m≠n)表示的曲线是椭圆.(　　)
题组二　双基自测5.(2023·辽宁丹东模拟)椭圆 +y2=1的一个短轴端点到一个焦点的距离为　　　　　　　. 
7. 航天器的轨道有很多种,其中的“地球同步转移轨道”是一个椭圆轨道,而且地球的中心正好是椭圆的一个焦点.若地球同步转移轨道的远地点(即椭圆上离地球表面最远的点)与地球表面的距离为m,近地点与地球表面的距离为n,设地球的半径为r,用m,n,r表示出地球同步转移轨道的离心率.
题组(1)如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是(　　)A.椭圆 B.双曲线C.抛物线 D.圆
答案 (1)A　(2)20　8解析 (1)由条件知|PM|=|PF|,∴|PO|+|PF|=|PO|+|PM|=|OM|>|OF|.∴点P的轨迹是以O,F为焦点的椭圆.
规律方法 椭圆定义的应用(1)确认平面内与两定点有关的轨迹是否为椭圆.(2)当点P在椭圆上时,与椭圆的两焦点F1,F2组成的三角形通常称为“焦点三角形”,利用定义可求其周长,利用定义和余弦定理可建立|PF1|+|PF2|=2a与|PF1||PF2|之间的联系,通过整体代入可求其面积等.
考向1定义法求椭圆的标准方程例题已知两圆C1:(x-4)2+y2=169,C2:(x+4)2+y2=9,动圆M在圆C1内部且和圆C1相内切,和圆C2相外切,则动圆圆心M的轨迹方程为(　　)
答案 D解析 设圆M的半径为r,则|MC1|+|MC2|=(13-r)+(3+r)=16>8=|C1C2|,所以点M的轨迹是以C1,C2为焦点的椭圆.因为2a=16,2c=8,所以a=8,c=4,b2=a2-c2=48.
引申探究(变条件)若将本例题条件中的“和圆C2相外切”改为“和圆C2也内切”,其余不变,则动圆圆心M的轨迹方程为　　　　　　　　　. 解析 设圆M的半径为r,则|MC1|+|MC2|=(13-r)+(r-3)=10>8=|C1C2|,所以点M的轨迹是以C1,C2为焦点的椭圆.因为2a=10,2c=8,所以a=5,c=4,b2=a2-c2=9.故所求的轨迹方程为
考向2待定系数法求椭圆的标准方程
规律方法 求椭圆方程的方法与步骤
考向1椭圆的长轴、短轴、焦距、对称性
规律方法 求解与椭圆几何性质有关的问题时,要理清顶点、焦点、长轴长、短轴长、焦距等基本量的内在联系.
A.有相等的长轴长B.有相等的短轴长C.有相同的焦点D.有相等的焦距答案 D
答案 (1)A　(2)C
规律方法 求椭圆离心率(或其取值范围)的两种常用方法
(2)(2022·山东聊城一模)F1,F2是椭圆C的两个焦点,P是椭圆C上异于顶点的一点,I是△PF1F2的内切圆圆心.若△PF1F2的面积等于△IF1F2的面积的3倍,则椭圆C的离心率为　　　　　　　. 
考向3与椭圆有关的范围(最值)问题例题(2023·辽宁营口高三期末)设椭圆C: 的左焦点为F,直线l:y=kx(k≠0)与椭圆C交于A,B两点,则△AFB的周长的取值范围是(　　)A.(8,10)B.(16,20)C.(18,20)D.(16,18)
规律方法 与椭圆有关的最值或范围问题的求解策略