适用于新教材2024版高考数学一轮总复习第九章平面解析几何解答题专项五第2课时最值与范围问题课件北师大版

这是一份适用于新教材2024版高考数学一轮总复习第九章平面解析几何解答题专项五第2课时最值与范围问题课件北师大版，共38页。
考向1建立目标函数法求最值例题(12分)(2021·全国乙,理21)已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.(1)求p;(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求△PAB面积的最大值.
【教师讲评】 (1)根据题意写出点F,M的坐标及圆M的半径r,结合F与圆M上点的距离的最小值为4求解;(2)设出直线AB的方程,与抛物线方程联立,结合根与系数的关系及弦长公式得到|AB|,再根据点到直线的距离公式得到点P到直线AB的距离d,进而得到△PAB面积的表达式,结合二次函数的基本性质可求得△PAB面积的最大值.
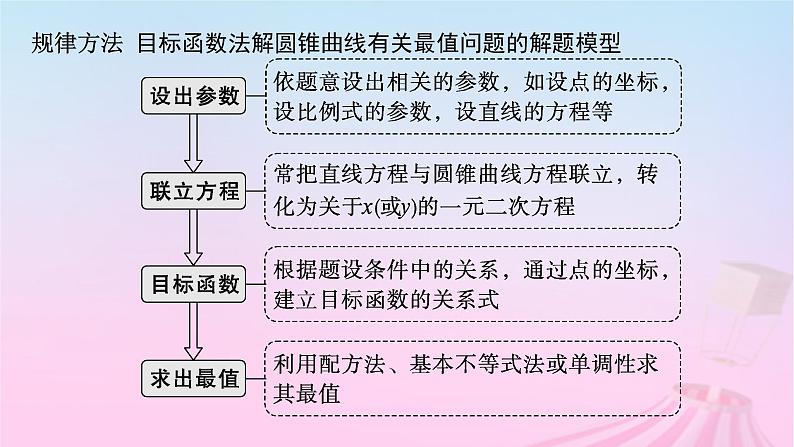
规律方法 目标函数法解圆锥曲线有关最值问题的解题模型
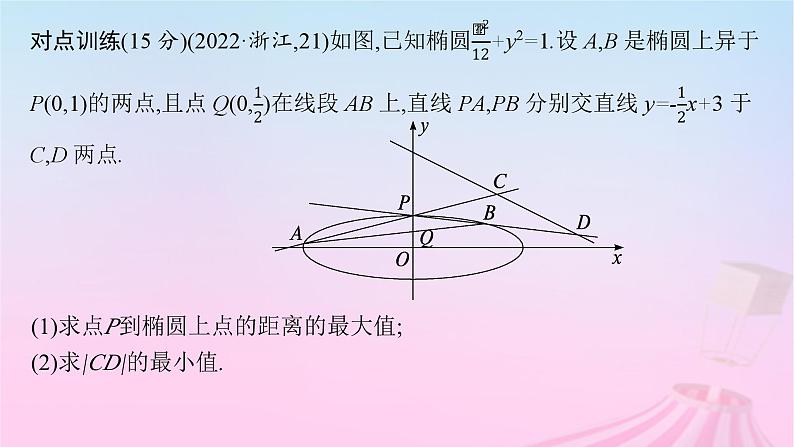
(1)求点P到椭圆上点的距离的最大值;(2)求|CD|的最小值.
考向2构造基本不等式法求最值(1)求椭圆E的标准方程;(2)设过点F2且倾斜角不为0的直线l与椭圆E的交点为A,B,求△F1AB面积最大时直线l的方程.
规律方法 构造基本不等式求最值的步骤
考向1构造不等式法求范围例题(2023·湖北武汉模拟)已知P是平面上的动点,且点P与F1(-2,0),F2(2,0)的距离之差的绝对值为2 .设点P的轨迹为曲线E.(1)求曲线E的方程;
规律方法 构造不等式求范围的三种常用方法
对点训练(2023·浙江嘉兴模拟)已知抛物线y2=2px(p>0)的焦点为F,点M是抛物线的准线x=-2上的动点.(1)求p的值和抛物线的焦点坐标;(2)设直线l与抛物线相交于A,B两点,且MF⊥AB,AF⊥MB,求直线l在x轴上的截距b的取值范围.
考向2构造函数法求范围
规律方法 利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.
对点训练已知抛物线C:y2=2px(p>0)的焦点为点F,点M(a,2 )在抛物线C上.(1)若|MF|=6,求抛物线的标准方程;(2)若直线x+y=t与抛物线C交于A,B两点,点N的坐标为(1,0),且满足NA⊥NB,原点O到直线AB的距离不小于 ,求p的取值范围.
设A(x1,y1),B(x2,y2).因为Δ=4(t+p)2-4t2=4p(p+2t)>0,所以x1+x2=2t+2p,x1x2=t2.因为NA⊥NB,所以(x1-1)(x2-1)+y1y2=0.