2022-2023学年云南省昆明市五华区八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年云南省昆明市五华区八年级（下）期末数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年云南省昆明市五华区八年级（下）期末数学试卷
一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
1. 如果 a−3有意义，则a的取值范围是(    )
A. a>3 B. a0
6. 下列各式中，运算正确的是(    )
A. 3 3− 3=3 B. (−2)2=−2 C. 2+ 3=2 3 D. 2× 8=4
7. 在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是(    )
A. AB//DC，AD=BC B. AB=DC，AD=BC
C. AO=CO，BO=DO D. AB//DC，AD//BC
8. 矩形具有而一般平行四边形不具有的性质是(    )
A. 对角线相等 B. 对边相等 C. 对角相等 D. 对角线互相平分
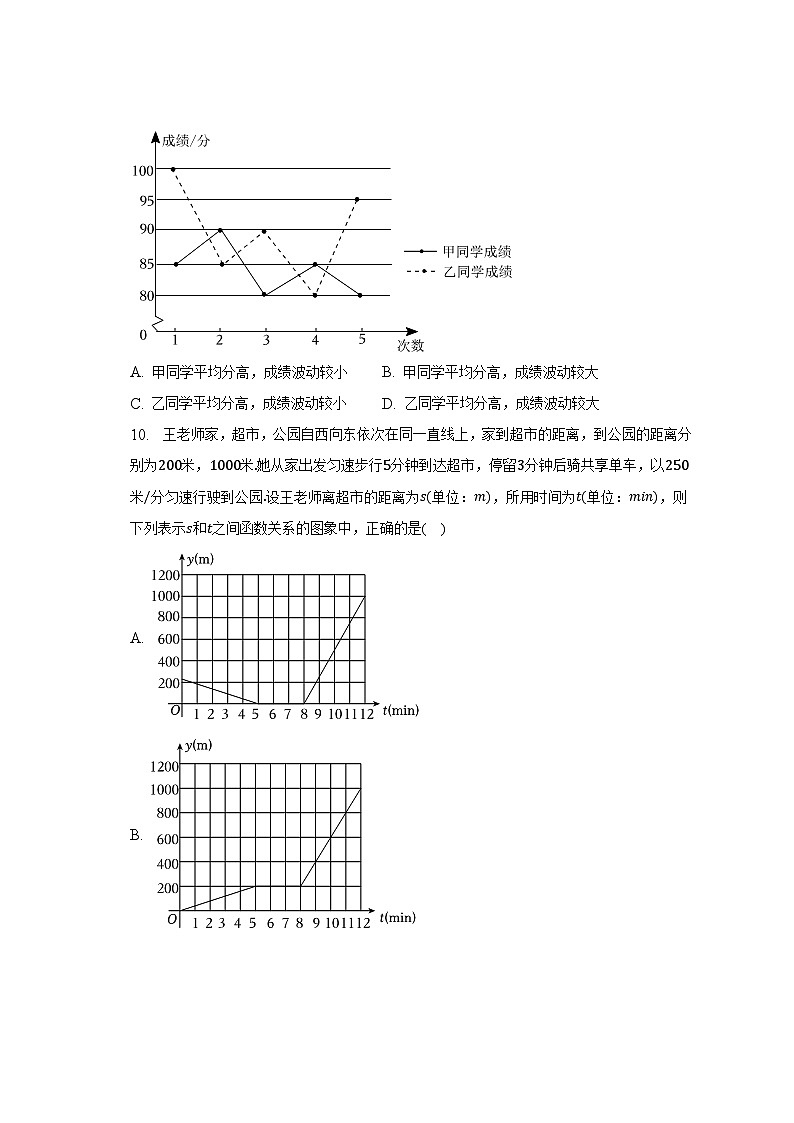
9. 如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名同学的成绩，下列说法正确的是(    )


A. 甲同学平均分高，成绩波动较小 B. 甲同学平均分高，成绩波动较大
C. 乙同学平均分高，成绩波动较小 D. 乙同学平均分高，成绩波动较大
10. 王老师家，超市，公园自西向东依次在同一直线上，家到超市的距离，到公园的距离分别为200米，1000米.她从家出发匀速步行5分钟到达超市，停留3分钟后骑共享单车，以250米/分匀速行驶到公园.设王老师离超市的距离为s(单位：m)，所用时间为t(单位：min)，则下列表示s和t之间函数关系的图象中，正确的是(    )
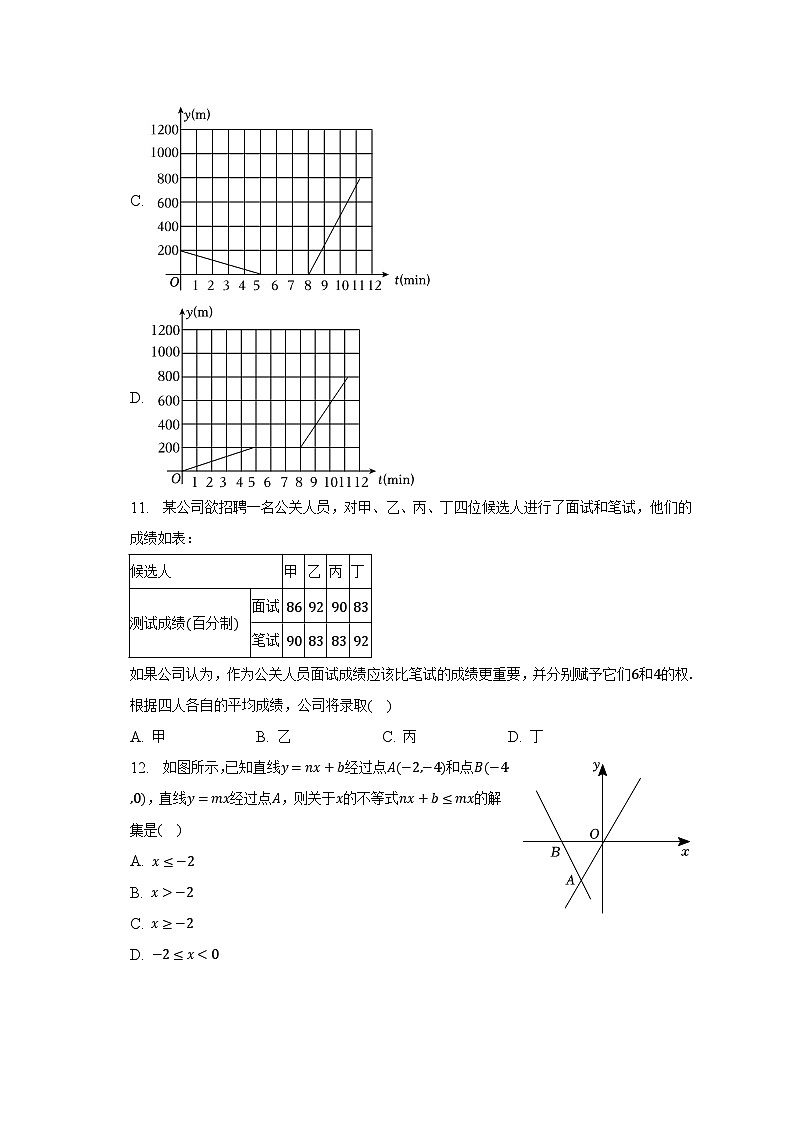
A.
B.
C.
D.
11. 某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：
候选人
甲
乙
丙
丁
测试成绩(百分制)
面试
86
92
90
83
笔试
90
83
83
92
如果公司认为，作为公关人员面试成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.根据四人各自的平均成绩，公司将录取(    )
A. 甲 B. 乙 C. 丙 D. 丁
12. 如图所示，已知直线y=nx+b经过点A(−2,−4)和点B(−4,0)，直线y=mx经过点A，则关于x的不等式nx+b≤mx的解集是(    )
A. x≤−2
B. x>−2
C. x≥−2
D. −2≤x14，
∴乙的离散程度较高，不稳定，甲的离散程度较低，比较稳定；
故选：D．
分别求出甲、乙的平均数、方差，比较得出答案．
本题考查平均数、方差的计算方法，从统计图中获取数据，是正确计算的前提．

10.【答案】C 
【解析】解：由题意可得，王老师离超市的距离为s(单位：m)，所用时间为t(单位：min)，家到超市、超市到公园的距离分别为200m，800m，
∵王老师从家出发匀速步行5分钟到达超市，
∴这个过程y随x的增大而减小，
∵王老师到超市后，停留3min，
∴这个过程y随x的变化不改变，y的值都是0，
∵王老师250米/分匀速行驶到公园，
∴这个过程y随x的增大而增大，当x=5+3+800÷250=11.2时，y=800，
故选：C．
根据题意和题目中的数据，可以写出各段y随x的变化如何变化，然后即可判断哪个选项符合题意．
本题考查了函数的图象，利用数形结合思想解决问题是解题的关键．

11.【答案】B 
【解析】解：甲的平均成绩为：(86×6+90×4)÷10=87.6(分)，
乙的平均成绩为：(92×6+83×4)÷10=88.4(分)，
丙的平均成绩为：(90×6+83×4)÷10=87.2(分)，
丁的平均成绩为：(83×6+92×4)÷10=86.6(分)，
因为乙的平均分数最高，所以乙将被录取．
故选：B．
首先根据权重，可知每个人的成绩可以用(面试成绩×6+笔试成绩×4)÷10进行计算得到；再比较四个人成绩的高低，则成绩最高的人即为公司录取的人，从而解决问题．
本题考查加权平均数，解答本题的关键是明确加权平均数的计算方法，求出甲乙丙丁的成绩．

12.【答案】C 
【解析】解：由图象可知，当x≥−2时，直线y=nx+b在直线y=mx下方，
∴关于x的不等式nx+b≤mx的解集是x≥−2，
故选：C．
根据A点的坐标结合图象即可求解．
本题考查了一次函数与一元一次不等式，一次函数的性质，理解图象是本题的关键．

13.【答案】3 
【解析】解：原式= 18÷2= 9=3．
故答案为：3．
直接运用二次根式的除法法则进行计算即可．
本题考查了二次根式的除法．

14.【答案】 10 
【解析】解：∵四边形ABCD是正方形，
∴∠CBF+∠FBA=90°，AB=BC，
∵CF⊥BE，
∴∠CBF+∠BCF=90°，
∴∠BCF=∠ABE，
∵∠AEB=∠BFC=90°，AB=BC，
∴△ABE≌△BCF(AAS)
∴AE=BF，BE=CF，
∴AB= 1+9= 10．
故答案为： 10．
先利用AAS判定△ABE≌△BCF，从而得出AE=BF，BE=CF，最后得出AB的长．
此题主要考查了正方形的性质及全等三角形的判定方法，做题时要注意各个条件之间的关系并灵活运用．

15.【答案】3 5 
【解析】解：由折叠可知：DC=DC′，∠DC′A=∠C=90°，AC′=AC=6，
在Rt△ABC中，由勾股定理得：AB= AC2+BC2=10，
∴BC′=AB−AC′=4，
设BD=x，则CD=DC′=8−x，
在Rt△BDC′中，由勾股定理得：x2=42+(8−x)2，
∴x=5，
∴BD=5，CD=3，
∴AD= AC2+CD2= 62+32=3 5，
故答案为：3 5．
由勾股定理求出AB=10，由折叠的性质得出CD=DC′，∠C=∠AC′D=90°，AC′=AC=6，得出BC′=AB−AC′=4，∠BC′D=90°，设BD=x，则CD=DC′=8−x，在Rt△BDC′中，由勾股定理得出方程，可求BD长，由勾股定理可求AD的长．
本题考查了翻折变换的性质，勾股定理等知识；熟练掌握翻折变换的性质，由勾股定理得出方程是解题的关键．

16.【答案】53 
【解析】解：由题意得：
y=2x−1y=−x+3，
解得：x=43y=53，
当2x−1≥−x+3时，x≥43，
∴当x≥43时，y=min{2x−1,−x+3}=−x+3，
由图象可知：此时该函数的最大值为53；
当2x−1≤−x+3时，x≤43，
∴当x≤43时，y=min{2x−1,−x+3}=2x−1，
由图象可知：此时该函数的最大值为53；
综上所述，y=min{2x−1,−x+3}的最大值是当x=43所对应的y的值，
如图所示，当x=43时，y=53，
故答案为：53．
根据定义先列不等式：2x−1≥−x+3和2x−1≤−x+3，确定其y=min{2x−1,−x+3}对应的函数，画图象可知其最大值．
本题考查了新定义问题、一元一次不等式及一次函数的交点问题，认真阅读理解其意义，并利用数形结合的思想解决函数的最值问题．

17.【答案】解：( 6−3)( 6+3)+( 2−1)2
=( 6)2−32+( 2)2−2 2+1
=6−9+2−2 2+1
=−2 2． 
【解析】根据二次根式混合运算的法则计算即可．
本题考查了二次根式的混合运算，熟练掌握二次根式混合运算的法则是解题的关键．

18.【答案】解：连接AB，
∵AO=AB= 12+32= 10，OB= 22+42=2 10，
∴AO2+AB2=OB2，
∴∠OAB=90°，
∴△AOB是等腰直角三角形，
∴∠AOB=45°． 
【解析】根据勾股定理和勾股定理的逆定理即可得到结论．
本题考查了勾股定理，勾股定理的逆定理，等腰直角三角形判定和性质，熟练掌握勾股定理的逆定理是解题的关键．

19.【答案】6  91  甲 
【解析】解：(1)由题意可知，a=6，b=90+922=91，
故答案为：6；91；
(2)因为89