2023年河南省郑州市中牟县中考数学二模试卷（含解析）

这是一份2023年河南省郑州市中牟县中考数学二模试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年河南省郑州市中牟县中考数学二模试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. −4的倒数是(    )
A. 14 B. −14 C. 4 D. −4
2. 中牟县谋划2023年政府投资新建项目77个，总投资35.2亿元，年度计划投资13.7亿元.数据“13.7亿”用科学记数法表示为(    )
A. 13.7×108 B. 1.37×108 C. 1.37×109 D. 13.7×109
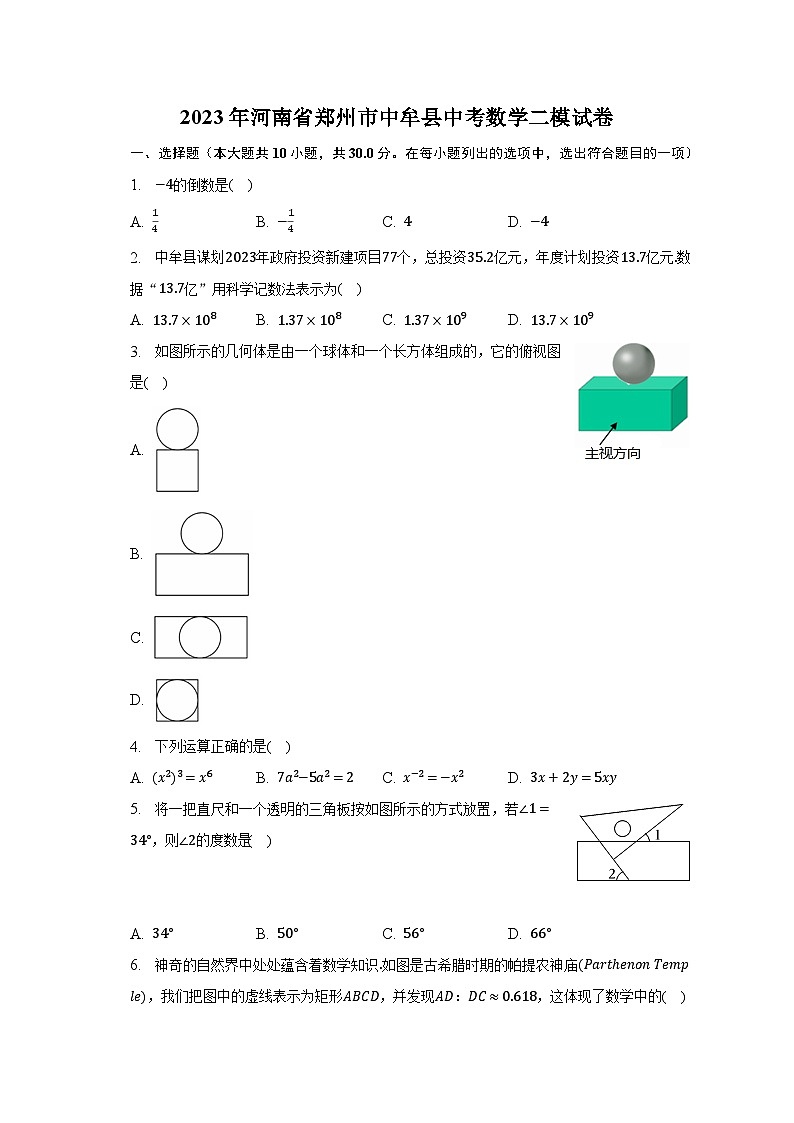
3. 如图所示的几何体是由一个球体和一个长方体组成的，它的俯视图是(    )
A.
B.
C.
D.
4. 下列运算正确的是(    )
A. (x2)3=x6 B. 7a2−5a2=2 C. x−2=−x2 D. 3x+2y=5xy
5. 将一把直尺和一个透明的三角板按如图所示的方式放置，若∠1=34°，则∠2的度数是(    )


A. 34° B. 50° C. 56° D. 66°
6. 神奇的自然界中处处蕴含着数学知识.如图是古希腊时期的帕提农神庙(Parthenon Temple)，我们把图中的虚线表示为矩形ABCD，并发现AD：DC≈0.618，这体现了数学中的(    )

A. 平移 B. 旋转 C. 轴对称 D. 黄金分割
7. 李萍经营了一家鞋店，一周内她销售了某牌子的女鞋30双，各种尺码鞋的销售量如下表所示，你认为李萍更应该关注鞋子尺码的(    )
尺码/cm
23
23.5
24
24.5
25
销售量/双
6
9
13
1
1

A. 平均数 B. 中位数 C. 众数 D. 方差
8. 若关于x的一元二次方程(m−1)x2+2x−1=0有两个实数根，则m的取值范围是(    )
A. m≥0 B. m>0 C. m≥0且m≠1 D. m>0且m≠1
9. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两(我国古代货币单位)；马三匹、牛五头，共价三十八两．问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为(    )
A. 4x+6y=383x+5y=48 B. 4x+6y=485x+3y=38 C. 4x+6y=483x+5y=38 D. 4x+6y=385x+3y=48
10. 如图，在平面直角坐标系中，已知点A(2,0)，∠OAB=120°，AB=AO=2，且点B在第一象限内，将△AOB绕点O顺时针旋转，每次旋转60°，则第2023次旋转后，点B的坐标是(    )


A. (3,− 3) B. (0,−2 3) C. (−3,− 3) D. (−3, 3)
二、填空题（本大题共5小题，共15.0分）
11. 分式−4x+2有意义的条件是______ ．
12. 计算： 4−(2023−π)0= ______ ．
13. 在化学课上，张萍老师为帮助学生正确理解物理变化与化学变化，将4种生活现象制成外表完全相同的卡片(如图)，然后将卡片背面向上洗匀从中随机抽取两张，则抽出的生活现象都是物理变化的概率是______ ．

14. 如图，在矩形ABCD中，AB=2，以BC为直径的圆恰好与AD相切于点F，将点F绕点C逆时针旋转，其旋转路径与BC交于点E.图中阴影部分的面积为______ ．


15. 如图，在正方形ABCD中，AB=4，点E为AB边的中点，点P是边BC上一动点，连接PE，沿PE折叠△PBE得到△PFE.当射线EF经过正方形ABCD的边的中点(不包括点E)时，BP的长为______ ．


三、解答题（本大题共8小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题5.0分)
(1)解不等式组：5x+1>3(x−1),①12x22.5°，于是可得射线EF不能经过AD的中点；
②当射线EF经过CD的中点M时，先证四边形BCME为矩形，进而可证△BEP为等腰直角三角形，从而可得出BP的长；
③当射线EF经过BC的中点M时，先由勾股定理求出EM=2 2，再由折叠的性质得FM=2 2−2，PM=2−BP，然后在Rt△PMF中由勾股定理即可求出BP的长．
本题主要考查正方形的性质，矩形的判定和性质，图形的折叠和性质，勾股定理的应用，解答此题的关键是进行分类讨论，根据三种不同情况分别画出图形，利用翻折的性质解决问题．

16.【答案】解：(1)解①得x>−2，
解②得xy1，
∵王斌每周去俱乐部打球2次，
∴王斌2023年去俱乐部打球的次数为3657×2≈104(次)，
∵104>80，
∴y2>y1，
∴他选择方案一所需费用更少． 
【解析】(1)利用待定系数即可求出y1关于x的函数解析式，再根据“方案二的描述”即可得出y2关于x的函数解析式；
(2)联立两函数解析式求出交点坐标为(80,1200)，由图象可知，当xy2，当x≥80时，y2>y1，再求出他一年去去俱乐部打球的次数，和80进行比较即可求解．
本题主要考查一次函数的应用、用待定系数法求一次函数解析式，理解题意，根据题意和图象正确求出一次函数解析式是解题关键．

20.【答案】解：(1)把x=2代入一次函数y=x+2，
∴y=4．
把x=2，y=4代入反比例函数y=kx，
∴k=8．
∴反比例函数的表达式为y=8x．
(2)将一次函数y=x+2的图象向下平移4个单位长度得到y=x−2．
又由题意可得，y=x−2y=8x．
∴x=4y=2或x=−2y=−4．
∴交点坐标为(4,2)，(−2,−4)． 
【解析】(1)将x=2代入y=x+2=4，故其中交点A的坐标为(2,4)，将(2,4)代入反比例函数表达式，即可求解；
(2)一次函数y=x+2的图象向下平移4个单位得到y=x−2，一次函数和反比例函数解析式联立，解方程组求得A、B的坐标．
本题考查了反比例函数与一次函数的交点，掌握一次函数图象上点的坐标特征和待定系数法求反比例函数的解析式是解题的关键．

21.【答案】PE=PF 
【解析】(1)解：图形如图所示：

(2)已知：PE，PF与⊙O相切于点E，F.求证：PE=PF．
证明：∵PE，PF是⊙O的切线，
∴PE⊥OE，PF⊥OF，
∴∠PEO=∠PFO=90°，
在Rt△PEO和Rt△PFO中，
PO=POOE=OF，
∴Rt△PEO≌Rt△PFO(HL)，
∴PE=PF．
故答案为：PE=PF．
(1)根据要求作出图形；
(2)证明Rt△PEO≌Rt△PFO(HL)，可得结论．
本题考查作图−应用与设计作图，切线的性质，全等三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题−

22.【答案】解：(1)根据题意得，二次函数表达式表达式为y=−(x−14)2+916=−x2+12x+12，
∴二次函数表达式为y=−x2+12x+12；
(2)令y=0，则−x2+12x+12=0，
解得x1=−12(舍去)，x2=1，
∴水池的半径至少要1米才能使喷出的水流不至于落在池外． 
【解析】(1)根据题意直接得出二次函数表达式；
(2)令y=0，解关于x的一元二次方程，求得正数解即可．
本题考查了二次函数的实际应用，解题的关键是从实际问题中抽象出二次函数模型，难度中等．

23.【答案】BP=CF 
【解析】(1)解：如图①，设BP交CF于点L，
∵将△BPC沿BP折叠，得到△BPE，
∴点E与点C关于直线BP对称，
∴BP垂直平分CE，
∴∠BLC=90°，
∵四边形ABCD是正方形，
∴BC=CD，∠BCP=∠D=90°，
∴∠PBC=∠FCD=90°−∠BCF，
∴△PBC≌△FCD(ASA)，
∴BP=CF，
故答案为：BP=CF．
(2)解：BP=MN，理由如下：
如图②，设BP交MN于点L，作CJ//MN交AD于点J，交BP于点K，
∵CM//JN，
∴四边形MCJN是平行四边形，
∴CJ=MN，
由折叠得点P与点B关于直线MN对称，
∴MN垂直平分BP，
∴∠PKC=∠PLM=90°，
∵∠BCP=∠D=90°，
∴∠BPC=∠CJD=90°−∠DCJ，
∵BC=CD，
∴△PBC≌△JCD(AAS)，
∴BP=CJ，
∴BP=MN．
(3)证明：如图③，连接BD、GD、GP，
∵AC垂直平分BD，
∴DG=BG，
∵DC=BC，CG=CG，
∴△DCG≌△BCG(SSS)，
∴∠GDC=∠GBC，
∵MN垂直平分BP，
∴PG=BG，
∴PG=DG，
∴∠GDC=∠GPD，
∴∠GBC=∠GPD，
∴∠GBC+∠GPC=∠GPD+∠GPC=180°，
∴∠BGP+∠BCP=360°−(∠GBC+∠GPC)=180°，
∴∠BGP=180°−∠BCP=90°，
∴GH=12BP=12MN，
∴MN=2GH．
(4)解：NG的长为=3 54，
理由：∵BC=DC=AB=6，点P是DC的中点，
∴PC=PD=12CD=12×6=3，
∴BP= BC2+PC2= 62+32=3 5，
∴BH=12BP=12×3 5=3 52，
∵∠BLM=∠BCP=90°，
∴MHBH=PCBC=tan∠PBC=36=12，
∴MH=12BH=12×3 52=3 54，
∵MN=BP=3 5，GH=12BP=3 52，
∴NG=MN−MH−GH=3 5−3 54−3 52=3 54．
(1)设BP交CF于点L，由折叠得BP垂直平分CE，则∠BLC=90°，由正方形的性质得BC=CD，∠BCP=∠D=90°，则∠PBC=∠FCD=90°−∠BCF，即可证明△PBC≌△FCD，得BP=CF，于是得到问题的答案；
(2)设BP交MN于点L，作CJ//MN交AD于点J，交BP于点K，则四边形MCJN是平行四边形，所以CJ=MN，再证明△PBC≌△JCD，则BP=CJ=MN；
(3)连接BD、GD、GP，由AC垂直平分BD，得DG=BG，而DC=BC，CG=CG，可证明△DCG≌△BCG，得∠GDC=∠GBC，再证明PG=DG，得∠GDC=∠GPD，则∠GBC=∠GPD，则∠GBC+∠GPC=∠GPD+∠GPC=180°，可推导出∠BGP=90°，则GH=12BP=12MN，所以MN=2GH；
(4)由BC=DC=AB=6，点P是DC的中点，得PC=12CD=3，由勾股定理得BP= BC2+PC2=3 5，则BH=12BP=3 52，由MHBH=PCBC=tan∠PBC=12，得MH=12BH=3 54，而MN=BP=3 5，GH=12BP=3 52，即可求得NG=MN−MH−GH=3 54．
此题重点考查正方形的性质、轴对称的性质、线段的垂直平分线的性质、全等三角形的判定与性质、勾股定理、锐角三角函数与解直角三角形等知识，此题综合性强，难度较大，属于考试压轴题．