2023年福建省宁德市蕉城区博雅培文学校中考数学三模试卷（含解析）

这是一份2023年福建省宁德市蕉城区博雅培文学校中考数学三模试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
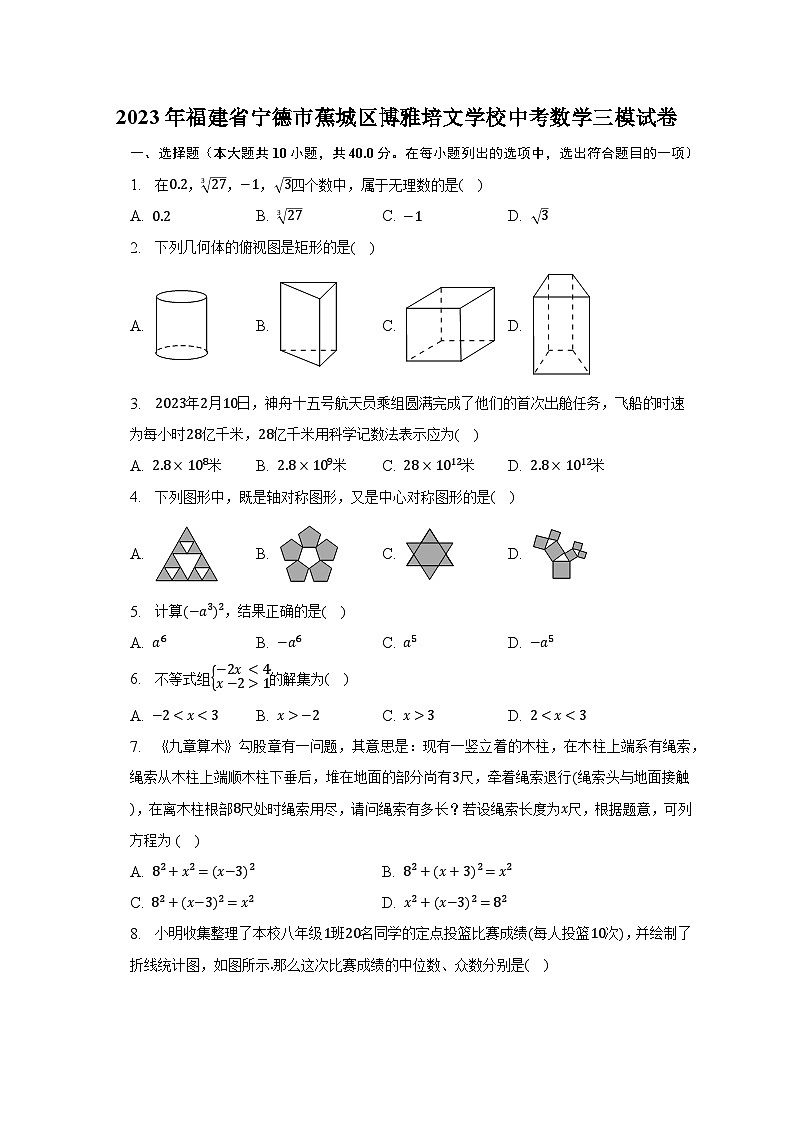
2023年福建省宁德市蕉城区博雅培文学校中考数学三模试卷
一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）
1. 在0.2，327，−1， 3四个数中，属于无理数的是(    )
A. 0.2 B. 327 C. −1 D. 3
2. 下列几何体的俯视图是矩形的是(    )
A. B. C. D.
3. 2023年2月10日，神舟十五号航天员乘组圆满完成了他们的首次出舱任务，飞船的时速为每小时28亿千米，28亿千米用科学记数法表示应为(    )
A. 2.8×108米 B. 2.8×109米 C. 28×1012米 D. 2.8×1012米
4. 下列图形中，既是轴对称图形，又是中心对称图形的是(    )
A. B. C. D.
5. 计算(−a3)2，结果正确的是(    )
A. a6 B. −a6 C. a5 D. −a5
6. 不等式组−2x1的解集为(    )
A. −23 D. 2(m−1)2+n，
∴(m−3)2−(m−1)2>0，
即−4m+8>0，
∴my2列出关于m的不等式即可解得答案．
本题考查了二次函数图象上点的坐标特征，解题的关键是根据已知列出关于m的不等式．本题属于基础题，难度不大．

11.【答案】a(a+1)(a−1) 
【解析】
【分析】
本题考查了提公因式法，公式法分解因式，提取公因式后利用平方差公式进行二次分解，注意要分解彻底．
先提取公因式a，再对余下的多项式利用平方差公式继续分解．
【解答】
解：a3−a
=a(a2−1)
=a(a+1)(a−1)．
故答案为a(a+1)(a−1)．  
12.【答案】15 
【解析】解：∵在我”“的”“中”“国”“梦”这5个字的卡片中只有1张写有“中”字，
∴这张卡片上面恰好写着“中”字的概率是15
故答案为：15．
由在我”“的”“中”“国”“梦”这5个字的卡片中只有1张写有“中”字，利用概率公式计算可得．
本题考查了统计与概率中概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．

13.【答案】30 
【解析】解：∵点D、E分别是AB，BC的中点，
∴DE是△ABC的中位线，
∴AC=2DE=5，
∴△ABC的周长=AB+AC+BC=13+5+12=30，
故答案为：30．
根据三角形中位线定理求出AC，根据三角形的周长公式计算即可．
本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．

14.【答案】y2x>34x，
∴获得比赛第三名的同学是E．
故答案为：E．
设B的得分为x分(x>0)，则A的得分为154x分，C的得分为72x分，D的得分为34x分，E的得分为3x分，将五人的成绩比较后即可得出结论．
本题考查了列代数式，根据各数量之间的关系，用含x的代数式表示出五人的成绩是解题的关键．

16.【答案】①② 
【解析】解：在AB上取点H，使AH=EC，连接EH，

∵∠HAE+∠AEB=90°，∠CEF+∠AEB=90°，
∴∠HAE=∠CEF，
又∵AH=CE，
∴BH=BE，
∴∠AHE=135°，
∵CF是正方形外角的平分线，
∴∠ECF=135°，
∴∠AHE=∠ECF，
在△AHE和△ECF中，
∠HAE=∠CEFAH=EC∠AHE=∠ECF，
∴△AHE≌△ECF(ASA)，
∴AE=EF，EH=CF，故①正确；
∵BE=BH，
∴EH= 2BE，
∴CF= 2BE，故②正确；
∵∠AHE=135°，
∴∠HAE+∠AEH=45°，
又∵AE=EF，
∴∠EAF=45°，
∴∠HAE+∠DAF=45°，
∴∠AEH=∠DAF，
∵∠AEH=∠EFC，
∴∠DAF=∠EFC，
而∠FEC不一定等于∠EFC，
∴∠DAF不一定等于∠FEC，故③错误；
∵△AHE≌△ECF，
∴S△AHE=S△CEF，
设AH=x，则S△AHE=12x⋅(1−x)=−12x2+12x，
当x=12时，S△AHE取最大值为18，
∴△CEF面积的最大值为18，故④错误，
故答案为：①②．
在AB上取点H，使AH=EC，连接EH，然后证明△AGE和△ECF全等，再利用全等三角形的性质即可得出答案．
本题主要考查正方形的性质和全等三角形的应用，关键是要能作出辅助线EG，构造出全等的三角形，要牢记全等三角形的性质．

17.【答案】解：原式=2−2+1
=1． 
【解析】利用绝对值的性质，算术平方根的定义，零指数幂进行计算即可．
本题考查实数的运算，熟练掌握相关的运算法则是解题的关键．

18.【答案】证明：∵∠ADE+∠3=∠1+∠B，∠1=∠3，
∴∠ADE=∠B，
∵∠1=∠2，
∴∠1+∠DAC=∠2+∠DAC，
即∠BAC=∠DAE，
∵∠B=∠4，
∴AB=AD，
在△ABC和△ADE中，∠BAC=∠DAEAB=AD∠B=∠ADE，
∴△ABC≌△ADE(ASA)，∴BC=DE． 
【解析】求出∠B=∠ADE，∠BAC=∠DAE，AB=AD，根据全等三角形的判定定理推出即可．
本题考查了全等三角形的性质和判定、等腰三角形的性质等知识；证明三角形全等是解题的关键．

19.【答案】解：原式=a+2−3a+2⋅(a+2)(a−2)(a−1)2，
=a−2a−1．
当a=0时，原式=−2−1=2． 
【解析】首先对括号内的分式进行通分相加，把除法转化为乘法，计算乘法即可化简，然后代入0或−1求解；
本题考查了分式的化简求值，正确进行通分、约分是关键，本题中要注意a不能取−2，2以及1．

20.【答案】20%  15%  B 
【解析】解：(1)56÷35%=160(人)，
b=24÷160=15%，
a=1−15%−35%−30%=20%，
B等级的人数为：160×20%=32(人)，
补全的条形统计图如图所示，

故答案为：20%，15%；
(2)所抽取员工下班路程的中位数落在等级B．
故答案为：B；
(3)900×(30%+15%)=405(人)，
答：估计该公司大约有405人可以优先选择共享单车．
(1)由两个统计图可知道A等级的有56人，占调查人数的35%，可求出调查人数，进而求出D等级所占的百分比，和B等级的百分比，再求出B等级的人数，从而补全条形统计图、以及扇形统计图中B、D所占的百分比．
(2)A等级占35%，B等级的占20%，从高到低，中位数应落在50%的组，因此落在B组．
(3)样本估计总体，样本中“在6公里以上“占(30%+15%)”估计总体中的也占45%，进而求出人数．
本题考查条形统计图、扇形统计图的特点及制作方法，从两个统计图中获取数量和数量之间的关系式解决问题的关键，样本估计总体是统计中常用的方法．

21.【答案】(1)证明：如图，连接AE．

∵AB是圆O的直径，
∴∠AEB=90°，
即AE⊥BC．
又∵AB=AC，
∴AE是边BC上的中线，
∴BE=CE；

(2)解：∵AB=6，
∴OA=3．
又∵OA=OD，∠BAC=54°，
∴∠AOD=180°−2×54°=72°，
∴AD的长为：72×π×3180=6π5． 
【解析】本题考查了圆周角定理、弧长的计算以及等腰三角形的判定与性质．通过作辅助线，利用圆周角定理(或圆半径相等)的性质求得相关角的度数是解题的难点．
(1)如图，连接AE，利用圆周角定理推知AE是等腰△ABC的垂线，结合等腰三角形的性质证得结论；
(2)如图，连接OD，利用等腰三角形的性质和三角形内角和定理可以求得圆心角∠AOD的度数，然后利用弧长公式进行解答．

22.【答案】解：(1)设A款保温杯销售单价是x元，则B款保温杯销售单价是(x+10)元，
根据题意得：960x=1200x+10，
解得x=40，
经检验，x=40是原方程的解，
∴x+10=40+10=50，
答：A款保温杯销售单价是40元，B款保温杯销售单价是50元；
(2)设这批保温杯的销售利润是w元，购进A款保温杯m个，则购进B款保温杯(120−m)个，
∵A款保温杯的数量不少于B款保温杯数量的一半，
∴m≥12(120−m)，
解得m≥40，
根据题意得：w=(40−30)m+(50−35)(120−m)=−5m+1800，
∵−5