初中数学人教版九年级上册22.3 实际问题与二次函数公开课ppt课件

这是一份初中数学人教版九年级上册22.3 实际问题与二次函数公开课ppt课件，共4页。
　21.2.4解一元二次方程一．选择题1．若关于x的方程x2+3x+a=0有一个根为1，则另一个根为（　　）A．﹣4 B．2 C．4 D．﹣32．设x1，x2是方程x2﹣4x+m=0的两个根，且x1+x2﹣x1x2=1，那么m的值为（　　）A．2 B．﹣3 C．3 D．﹣23．设ɑ，β是一元二次方程x2+2x﹣3=0的两个根，则ɑβ的值是（　　）A．3 B．﹣3 C．2 D．﹣2二．填空题4．写出方程x2-x-1=0的一个正根__________。5.若x1，x2是方程x2+2x﹣3=0的两根，则x1+x2=　　。6.已知x=（b2-4c＞0），则x2+bx+c的值为_____。7. 已知b＜a＜0，且__________。8. 方程x2-|x|-1=0的根是________。三．解答题9．设a，b是方程x2+x﹣2016=0的两个不相等的实数根．（1）a+b=　　；ab=　　；（2）求代数式a2+2a+b的值．10. 已知x1，x2是一元二次方程x2-5x-3=0的两个根，求：（1）x12+x22（2）11.已知方程x2+kx+k+2=0的两个实数根是x1、x2且x12+x22=4，求k的值。 12. 已知关于x的一元二次方程(2m−1)x2−2x+1＝0有两个不相等的实数根．（1）求m的取值范围；
（2）                         参考答案一．选择题1．A；2．C；3．B；二．填空题4．5.﹣2； 6.0;7. 8. 三．解答题9. 解：（1）∵a，b是方程x2+x-2016=0的两个不相等的实数根∴a+b=-1；ab=-2016；故答案为：-1．-2016；∴a2+2a+b=-1+2016=2015．10.解：∵x1，x2是一元二次方程x2-5x-3=0的两个实数根，∴x1+x2=5，x1•x2=-3；
（1）x12+x22=（x1+x2）2-2x1x2
=52-2×（-3）
=25+6
=31；
（2）∵（x2-x1）2=x12+x22-2x1x2
=31-2×（-3）
=37，
∴x2-x1=±，
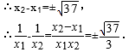 11.解：由根与系数的关系得  x1+x2=-k， x1x2=k+2  又  x12+ x2 2 = 4   即(x1+ x2)2 -2x1x2=4   k2- 2(k+2）=4  k2-2k-8=0    解得：k=4  或k=－2∵ △= k2-4k-8当k=4时， △＜0当k=-2时，△＞0∴ k=-212.