

初中数学人教版九年级上册24.1.4 圆周角精品ppt课件
展开 22.3.3实际问题与二次函数 第三课时
一.选择题
1.美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线y=﹣x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
A.y=﹣x2+x+1 B.y=﹣x2+x﹣1
C.y=﹣x2﹣x+1 D.y=﹣x2﹣x﹣1
2. 如图,一场篮球赛中,篮球运动员跳起投篮,已知球出手时离地面高2.2m,与篮圈中心的水平距离为8m,当球出手后水平距离为4m时达到最大高度4m,篮圈运行的轨迹为抛物线的一部分,篮圈中心距离地面3m,运动员发现未投中,若假设出手的角度和力度都不变,要使此球恰好通过篮圈中心,运动员应该跳得( )
A.比开始高0.8m B.比开始高0.4m
C.比开始低0.8m D.比开始低0.4m
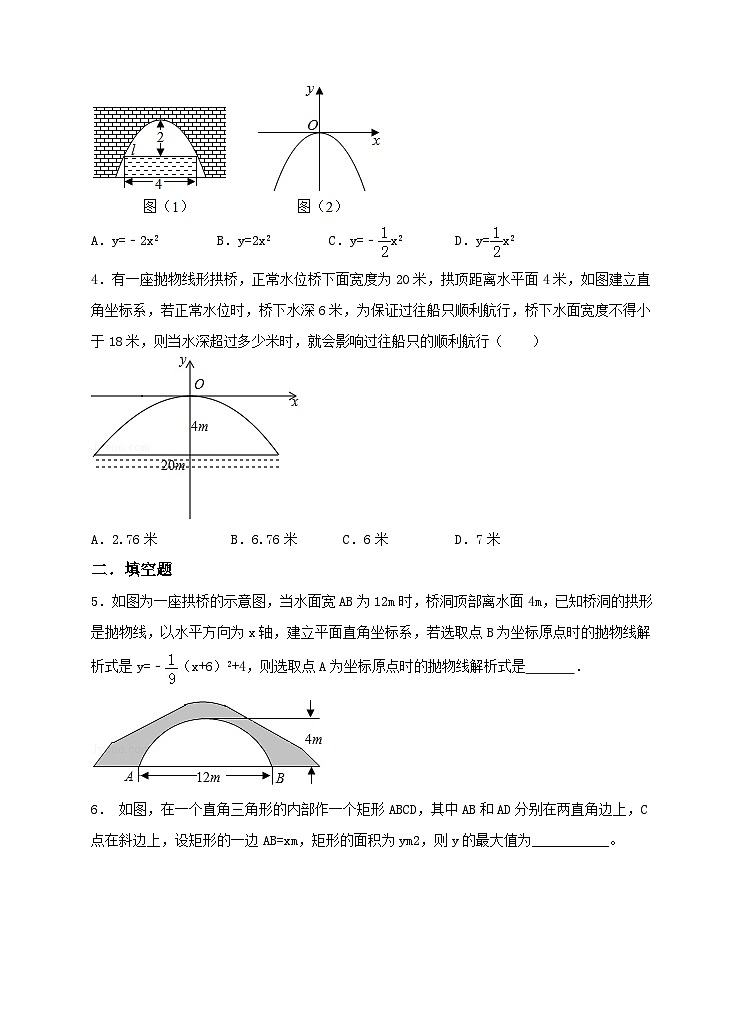
3.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣2x2 B.y=2x2 C.y=﹣x2 D.y=x2
4.有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
A.2.76米 B.6.76米 C.6米 D.7米
二.填空题
5.如图为一座拱桥的示意图,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点B为坐标原点时的抛物线解析式是y=﹣(x+6)2+4,则选取点A为坐标原点时的抛物线解析式是 .
6. 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上,C点在斜边上,设矩形的一边AB=xm,矩形的面积为ym2,则y的最大值为___________。
7.设计师以y=2x2﹣4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE= .
8.世界羽联在4日公布了最新一期世界排名,国羽依旧在男单、女双和混双三项排在头名位置.谌龙男单排名第一.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图2).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系y=﹣x2+x+,则羽毛球飞出的水平距离为 米.
三.解答题
9.(2017•金华)甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点O的水平距离为7m,离地面的高度为m的Q处时,乙扣球成功,求a的值.
10.(2017•德州)随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?
11.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
12.如图是一个抛物线形拱桥的示意图,桥的跨度AB为100米,支撑桥的是一些等距的立柱,相邻立柱的水平距离为10米(不考虑立柱的粗细),其中距A点10米处的立柱FE的高度为3.6米.
(1)求正中间的立柱OC的高度;
(2)是否存在一根立柱,其高度恰好是OC的一半?请说明理由.
参考答案
一.选择题
1.A.
2.A.
3.C.
4. B.
二.填空题
5.y=﹣(x﹣6)2+4.
6.300m2
7.11.
8.5.
三.解答题
9.【解答】解:(1)①当a=﹣时,y=﹣(x﹣4)2+h,
将点P(0,1)代入,得:﹣×16+h=1,
解得:h=;
②把x=5代入y=﹣(x﹣4)2+,得:y=﹣×(5﹣4)2+=1.625,
∵1.625>1.55,
∴此球能过网;
(2)把(0,1)、(7,)代入y=a(x﹣4)2+h,得:
,
解得:,
∴a=﹣.
10.【解答】解:(1)如图所示:以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系,
设抛物线的解析式为
:y=a(x﹣1)2+h,
代入(0,2)和(3,0)得:,
解得:,
∴抛物线的解析式为:y=﹣(x﹣1)2+;
即y=﹣x2+x+2(0≤x≤3);
(2)y=﹣x2+x+2(0≤x≤3),
当x=1时,y=,
即水柱的最大高度为m.
11.【解答】解:(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x﹣6)2+h过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣,
故y与x的关系式为:y=﹣(x﹣6)2+2.6,
(2)当x=9时,y=﹣(x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,,
解得:x1=6+2>18,x2=6﹣2(舍去)
故会出界;
(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得:,
此时二次函数解析式为:y=﹣(x﹣6)2+,
此时球若不出边界h≥,
当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:
,
解得:,
此时球要过网h≥,
故若球一定能越过球网,又不出边界,h的取值范围是:h≥.
12.(2012•乌鲁木齐)如图是一个抛物线形拱桥的示意图,桥的跨度AB为100米,支撑桥的是一些等距的立柱,相邻立柱的水平距离为10米(不考虑立柱的粗细),其中距A点10米处的立柱FE的高度为3.6米.
(1)求正中间的立柱OC的高度;
(2)是否存在一根立柱,其高度恰好是OC的一半?请说明理由.
【解答】解:(1)根据题意可得中间立柱OC经过AB的中点O.
如图,以点O为原点,以AB所在的直线为x轴,建立直角坐标系.
问题转化为求点C的纵坐标.
|OF|=40(米),故B(50,0),E(﹣40,3.6)
设抛物线的解析式为y=ax2+c
∴解得:
∴y=﹣x2+10,当x=0时,y=10
即正中间的立柱OC的高度是10(米);
(2)设存在一根立柱的高度是OC的一半,即这根立柱的高度是5米.
则有﹣x2+10=5.解得:x=±25
∵相邻立柱之间的间距为10米.最中间的立柱OC在y轴上,
根据题意每根立柱上的点的横坐标为10的整数倍,
∴x=±25与题意不符,
∴不存在一根立柱,其高度恰好是OC高度的一半.
初中人教版24.1.4 圆周角说课ppt课件: 这是一份初中人教版24.1.4 圆周角说课ppt课件,共18页。PPT课件主要包含了学习目标,圆周角定理的推导,针对训练等内容,欢迎下载使用。
数学九年级上册24.1.4 圆周角背景图课件ppt: 这是一份数学九年级上册24.1.4 圆周角背景图课件ppt,共18页。PPT课件主要包含了合作探究,知识点一,知识点二,∠ACB,∠AOB,∠A∠C,精炼提升,知识点三,COA,同弧或等弧等内容,欢迎下载使用。
人教版七年级上册4.3.1 角教学ppt课件: 这是一份人教版七年级上册4.3.1 角教学ppt课件,共20页。PPT课件主要包含了知识回顾,创设情境引入新知,自主预习,自主探究,角的表示,知识梳理,随堂练习,填一填等内容,欢迎下载使用。













