

初中人教版22.1.1 二次函数优秀第三课时教案
展开人教版数学九年级上22.1.3二次函数y=a(x-h)2+k的图像和性质教学设计
课题
22.1.3二次函数的图像和性质
单元
第二十一章
学科
数学
年级
九年级上
学习
目标
情感态度和价值观目标
引导学生养成全面看问题、分类讨论的学习习惯,通过直观多媒体演示和学生动手作图、分析,激发学生学习数学的积极性。
能力目标
1、通过对二次函数一般形式的分类与图像关系的研究,培养学生的动手操作、观察、分析、分类讨论、归纳概括的能力;
2、体会运用“特殊到一般”、“数形结合”的数学思想方法。
知识目标
1.会用描点法画出二次函数y = a(x –h)2+k 的图象;
2.通过图象了解二次函数的图象特征和性质.
3.会确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
重点
观察图象,得出二次函数y = a(x–h)2的图象特征和性质.
难点
1. 观察图象,得出图象特征和性质.
2. 理解二次函数y=a(x-h)2、y=ax2之间的关系.
学法
自主思考、协作讨论、类比学习法
教法
启发引导、探究交流
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
一、复习回顾:
回顾y = ax2的图象和性质:
1.二次函数 y = ax2的图象是什么?
2.它具有怎样的图象特征和性质?
3.你是怎么研究的?
通过回忆旧知、提问问题引发学生思考,导入本课主题。
帮助学生回忆已学知识,在 基础上引导学习新知。
讲授新课
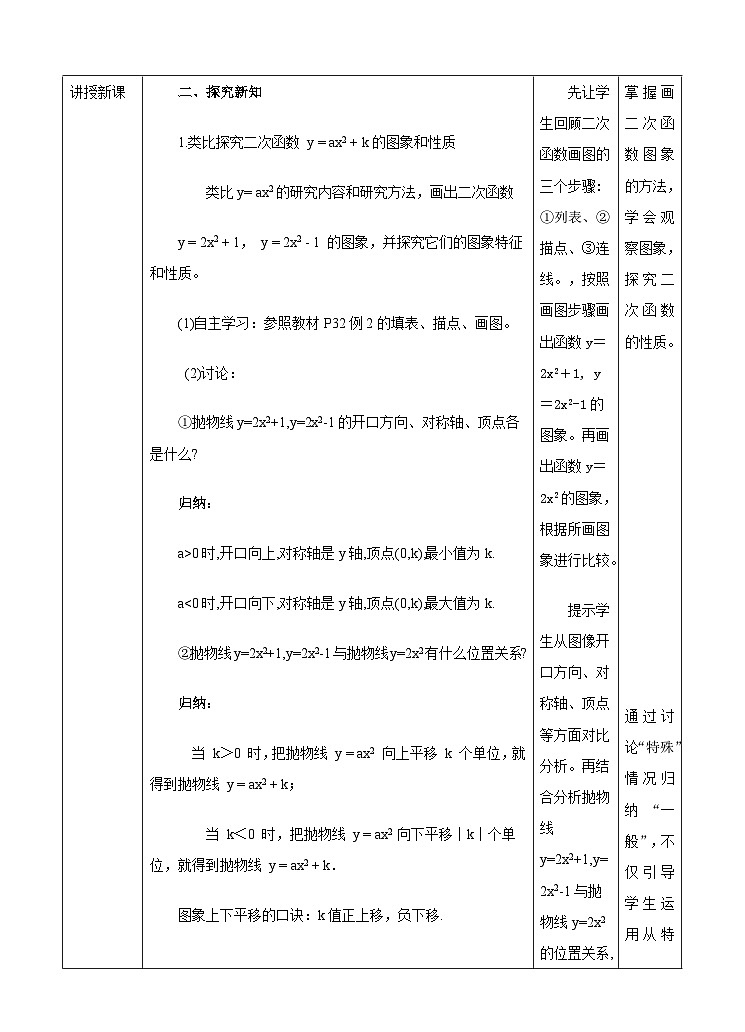
二、探究新知
1.类比探究二次函数 y = ax2 + k的图象和性质
类比y= ax2的研究内容和研究方法,画出二次函数
y = 2x2 + 1, y = 2x2 - 1 的图象,并探究它们的图象特征和性质。
(1)自主学习:参照教材P32例2的填表、描点、画图。
(2)讨论:
①抛物线y=2x2+1,y=2x2-1的开口方向、对称轴、顶点各是什么?
归纳:
a>0时,开口向上,对称轴是y轴,顶点(0,k),最小值为k.
a<0时,开口向下,对称轴是y轴,顶点(0,k),最大值为k.
②抛物线y=2x2+1,y=2x2-1与抛物线y=2x2有什么位置关系?
归纳:
当 k>0 时,把抛物线 y = ax2 向上平移 k 个单位,就得到抛物线 y = ax2 + k;
当 k<0 时,把抛物线 y = ax2 向下平移|k|个单位,就得到抛物线 y = ax2 + k.
图象上下平移的口诀:k值正上移,负下移.
(3)归纳与总结:
通过对二次函数 y = 2x2 + 1, y = 2x2 - 1 的探究,你能说出二次函数 y = ax 2 + k(a>0)的图象特征和性质吗?
一般地,当 a>0 时,抛物线 y = ax2 + k 的对称轴是 y 轴,顶点是(0,k),开口向上,顶点是抛物线的最低点,a 越大,抛物线的开口越小.当 x<0 时, y 随 x 的增大而减小,当 x>0 时, y 随 x 的增大而增大.
当 a<0 时,抛物线 y = ax2 + k 的对称轴是 y 轴,顶点是(0,k),开口向下,顶点是抛物线的最高点,a 越小,抛物线的开口越小.当 x<0 时, y 随 x 的增大而增大,当 x>0 时, y 随 x 的增大而减小.
完成相应练习
2. 类比探究二次函数y=a(x-h)2的图象和性质
画出二次函数y=-2,y=-2,y=-2的图象,并探究它们的图象特征和性质。
(1)自主学习:参照教材P33-34“探究”的填表、描点、画图。
(2)讨论:
①观察y=-(x+1)2,y=-(x-1)2的图象,分别指出他们的开口方向、对称轴、顶点。
抛物线y=- (x+1)2的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,把它记作x=-1,顶点是(-1,0);抛物线y=- (x-1)2的开口向下,对称轴是x=1,顶点是(1,0).
②y=-2,y=-2与抛物线y=-2有什么关系?
归纳:抛物线y=a(x-h)2与抛物线y=ax2有什么关系?
抛物线y=a(x-h)2与y=ax2形状相同,位置不同.
当h>0时,把抛物线y=ax2向右平移h个单位,可以得到抛物线y=a(x-h)2;
当h<0时,把抛物线y=ax2向左平移∣h∣个单位,可以得到抛物线y=a(x-h)2.
图象左右平移的口诀:h值正右移,负左移.
(3)归纳与总结:
y=a(x-h)2的图像性质:
a>0,开口向____,当x=___时,函数y有最___值=____,在对称轴的左侧,y随x的增大而____,在对称轴的右侧,y随x的增大而____.
a<0,开口向____,当x=____时,函数y有最___值=____,在对称轴的左侧,y随x的增大而____,在对称轴的右侧,y随x的增大而_____.
完成相应练习
3. 类比探究二次函数y=a(x-h)2+k的图象和性质
(1)自主学习:
在同一直角坐标系中,画出二次函数y=-x2,y=-x2-1,y=-(x+1)2-1的图象,并分别指出它们的开口方向、对称轴和顶点.
(2)讨论:
怎样移动抛物线y=-x2就可以得到抛物线y=-(x+1)2-1 ?
请你思考:还有其他的平移方法吗?
(3)归纳与总结:
二次函数y=a(x-h)2+k的图象特征和性质
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h,k的值来决定.
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下.
(2)对称轴是x=h.
(3)顶点是(h,k).
从二次函数y=a(x-h)2+k的图象可以看出:如果a>0,当x<h时,y随x的增大而减小,当x>h时,y随x的增大而增大;如果a<0,当x<h时,y随x的增大而增大,当x>h时,y随x的增大而减小.
练习1.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则函数坐标为( )
A.(-2,-1) B.(-2,1)
C.(2,-1) D.(2,1)
2.要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
先让学生回顾二次函数画图的三个步骤:①列表、②描点、③连线。,按照画图步骤画出函数y=2x2+1, y=2x2-1的图象。再画出函数y=2x2的图象,根据所画图象进行比较。
提示学生从图像开口方向、对称轴、顶点等方面对比分析。再结合分析抛物线y=2x2+1,y=2x2-1与抛物线y=2x2的位置关系,总结出二次函数y = ax2 + k的图象性质。
教师引导学生根据画函数图象的步骤画出函数的图象,交流合作,各组选派代表发表意见
学生观察所画的函数图象,互相交流、探讨,再让学生发表各自的见解,教师补充完善。
学生交流讨论并归纳出y=a(x-h)2的图像特点和性质,教师补充不足。
教师引导学生列表并画图,观察、认识这三个函数之间的关系,然后组织学生分组讨论,互相交流,让各组代表发言.
讨论总结,归纳出二次函数y=a(x-h)2+k的图象特征和性质。
掌握画二次函数图象的方法,学会观察图象,探究二次函数的性质。
通过讨论“特殊”情况归纳 “一般”,不仅引导学生运用从特殊到一般的学习方法,还培养了学生的交流沟通能力、总结归纳能力。
性质归纳是学生经历从特殊到一般,具体到抽象以及数学表达能力的由实践上升到理论训练。
再次运用类比法研究更复杂的二次函数图像,巩固了研究方法。
再次体会“从特殊到一般”数学数学方法。
课堂练习
1. y=x2+2的对称轴是直线( )
A.x=2 B.x=0
C.y=0 D.y=2
2 .关于二次函数y=2x2+3,下列说法中正确的是( )
A.它的开口方向是向下
B.当x<﹣1时,y随x的增大而减小
C.它的顶点坐标是(2,3)
D.当x=0时,y有最大值是3
3.已知函数图象如图所示,根据图象可得:
(1)抛物线顶点坐标___________;
(2)对称轴为________;
(3)当x=____时,y有最大值是_____;
(4)当________时,y随着x得增大而增大.
(5)当____________时,y>0.
4.将函数y=3x+1的图象向______平行移动_____个单位,可使它经过点(1,-1).
5.若将函数y=2x2的图象向右平行移动1个单位,再向上平移5个单位,可得到________________。
讨论交流,通过练习,进一步理解并掌握新知。
通过练习巩固本课所学,创设学生活动的机会,及时反馈知识的掌握情况。
课堂小结
通过本节课的内容,你有哪些收获?
(2)对称轴是x=h.
(3)顶点是(h,k).
(4)平移规律:h值正右移,负左移;k值正上移,负下移.
学会总结学习收获,巩固知识点,理清知识间的联系。
让学生来谈本节课的收获,培养学生自我检查、自我小结的良好习惯,将知识进行整理并系统化。
初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x-h)2+k的图象和性质教案及反思: 这是一份初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x-h)2+k的图象和性质教案及反思,共4页。教案主要包含了提出问题,分析问题,解决问题,做一做,小结,作业等内容,欢迎下载使用。
初中数学人教版九年级上册22.1.1 二次函数公开课教案设计: 这是一份初中数学人教版九年级上册22.1.1 二次函数公开课教案设计,共7页。
初中数学22.1.3 二次函数y=a(x-h)2+k的图象和性质第2课时教案设计: 这是一份初中数学22.1.3 二次函数y=a(x-h)2+k的图象和性质第2课时教案设计,共2页。













