数学九年级上册22.3 实际问题与二次函数精品第二课时教案

导入新课

    一、情境导入

设疑：观看商场的促销广告、电商广告页面，商家做广告的目的是什么？

如果你是商场经理，你该如何定价才能获得最大利润？

揭示课题：商品利润问题

教师出示各种促销图片，设疑，激发学生探究的欲望，进而揭示课题。

  从身边常见的生活实际情境入手，创设问题情境，激发学生的求知欲。

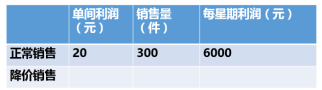
讲授新课

二、探究新知

问题1：某商品现在的售价为每件60元，每星期可卖出300件，已知商品的进价为每件40元，则每星期销售额是_____元，销售利润______元.

涉及到的数量关系：

（1）销售额=售价×销售量;

（2）利润=销售额-总成本=单件利润×销售量;

（3）单件利润=售价-进价.

问题2： 某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出20件，已知商品的进价为每件40元，如何定价才能使利润最大？

（1）降价：①设每件降价x元，则每星期售出商品的利润y元随之变化：

建立函数关系式：

②自变量x的取值范围如何确定？

③降价多少元时，利润y最大，是多少？

（2）涨价：①设每件涨价n元，则每星期售出商品的利润m元随之变化：

建立函数关系式：

②自变量n的取值范围如何确定？

③涨价多少元时，利润m最大，是多少？

由(1)(2)的探究及现在的销售情况,你知道应该如何定价能使利润最大了吗?

学生分小组合作探究,教师提供题干中涉及到的“数量关系”引导学生分步探究。

学生分组探究，老师设疑引导学生逐步解决问题。

由浅入深的例题设计，符合学生的实际认知过程，逐步提升学生分析和解决问题的能力，为运用二次函数解决商品利润问题做铺垫。

三、举一反三

变式：已知该T恤的进价为每件40元，售价是每件 60元，每星期可卖出300件。市场调查反映：每涨价1元，每星期要少卖出10件，若厂家规定促销期间每件售价不能超过64元，则销售单价定为多少时，商场可获得最大利润？最大利润是多少？

探究归纳：

求解最大利润问题的一般步骤：

（1）建立利润与价格之间的函数关系式：

运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”

（2）结合实际意义，确定自变量的取值范围；

（3）在自变量的取值范围内确定最大利润：

可以利用配方法或公式求出最大利润；也可以画出函数的简图，利用简图和性质求出.

教师引导学生共同用函数图象法来解决。师生共同探究，结合图象分析自变量的取值范围，进而计算出总利润。

结合解题思路，教师引导学生总结解答本类题型的一般步骤。

通过变式解答习题，加强学生解决商品利润问题的应用能力。

师生共同总结解题步骤，个学生体会总结学习规律的成就感。

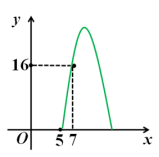
四、学以致用

某种商品每天的销售利润y（元）与销售单价x(元）之间满足关系：y=ax2+bx-75.其图象如图.

（1）销售单价为多少元时，该种商品每天的销售利润最大？最大利润是多少元？

（2）销售单价在什么范围时，该种商品每天的销售利润不低于16元？

通过实际应用练习使用二次函数解决商品利润问题的过程。巩固交流解题步骤与技巧。

通过解决实际问题，进一步巩固二次函数在实际商品利润问题中的运用。

课堂练习

1.山东全省2016年国庆假期旅游人数增长12.5%，其中尤其是乡村旅游最为火爆．泰山脚下的某旅游村，为接待游客住宿需要，开设了有100张床位的旅馆，当每张床位每天收费100元时，床位可全部租出，若每张床位每天收费提高20元，则相应的减少了10张床位租出，如果每张床位每天以20元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天最合适的收费是（　　）

A．140元     B．150元     C．160元        D．180元

2．某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100-x)件，应如何定价才能使利润最大？

3．某商店原来平均每天可销售某种水果200千克，每千克可盈利6元，为减少库存，经市场调查，如果这种水果每千克降价1元，则每天可多售出20千克．

（1）设每千克水果降价x元，平均每天盈利y元，试写出y关于x的函数表达式；

（2）若要平均每天盈利960元，则每千克应降价多少元？

学生独立完成，教师巡回检查，师生集体订正。

通过练习巩固本课所学，加深认识，深化提高，形成学生自己的解题技巧。

课堂小结

今天我们学习了哪些知识？

本节学习了商品利润问题的解题要点：

1.建立函数关系式：总利润=单件利润×销售量或总利润=总售价-总成本。

2.确定自变量取值范围：涨价:要保证销售量≥0； 降件：要保证单件利润≥0。

 3. 利用配方法或公式求最大值或利用函数简图和性质求出。

学会学生体会，反思，归纳总结本节的主要收获。

通过学生亲自解决实际问题的感受与经验，总结解题关键。