九年级上册第二十三章 旋转23.3 课题学习 图案设计公开课第三课时教案及反思

导入新课

   回想一下，上节课我们学了什么？

商品利润问题的解题要点：

1.建立函数关系式：总利润=单件利润×销售量或总利润=总售价-总成本。

2.确定自变量取值范围：涨价:要保证销售量≥0； 降件：要保证单件利润≥0。

3.利用配方法或公式求最大值或利用函数简图和性质求出最值。

 一、情境导入

思考：欣赏下列图片，你能想到什么？

分析：都有抛物线形物体。

教师教师提出问题，学生尝试回答。指导学生得出抛物线在我们生活中经常遇到。

  创设问题情境，联系生活，引导学生积极发现生活中的“数学”。

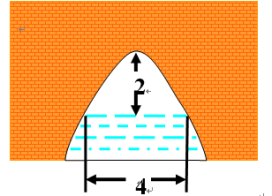
讲授新课

二、探究新知

探究1：如图是一座抛物线形拱桥,当拱桥顶离水面 2 m时,水面宽 4 m。水面下降 1 m, 水面宽度为多少？水面宽度增加多少 ？

教师提出问题：

（1）怎样把这个实际问题转化数学问题来解？

（2）求函数解析式的方法是什么？如何设这个函数解析式？

（3）你打算利用哪个点的坐标？这个点的坐标是什么？

教师引导学生思考，学生思考后回答，然后师生共同解题，写出解题过程。

探究2：

学生小组探讨：还可以怎样建立直角坐标系? 你能构建二次函数模型并列出解析式吗？

你能想出多少种方法？

探究3：

通过刚才的学习，你们能总结出用二次函数知识解决实物中抛物线形问题的一般步骤吗？

归纳总结：

解决抛物线型实际问题的一般步骤

(1)根据题意建立适当的直角坐标系；

(2)把已知条件转化为点的坐标；

(3)合理设出函数解析式；

(4)利用待定系数法求出函数解析式；

(5)根据求得的解析式进一步分析、判断并进行有关的计算.

学生通过思考探究，循序渐进找到解答实际问题的突破口，从而体会实际问题与数学模型的联系。

学生小组讨论，教师指导，学生回答，教师总结，及时鼓励表扬学生的奇思妙想。

学生思考回答，教师指导学生归纳。

通过为学生提供解决此类问题的思路，让学生在问题解决的过程中体会运用二次函数图像建模的数学思想。

举一反三，引导学生多角度思考问题，运用多种方法解决问题。

引导学生总结学习规律，体会探究乐趣。

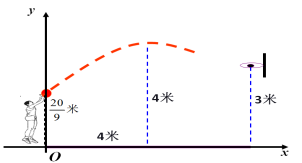
三、学以致用

在篮球赛中，姚小鸣跳起投篮，已知球出手时离地面高米，与篮圈中心的水平距离为8米，当球出手后水平距离为4米时到达最大高度4米，设篮 球运行的轨迹为抛物线，篮圈中心距离地面3米，他能把球投中吗？

学生独立完成，再合作交流，教师最后巡视指导。

巩固学生应用函数思想构建解析式，并解决实物中抛物线形问题的知识，进一步加强对所学知识的理解和掌握。

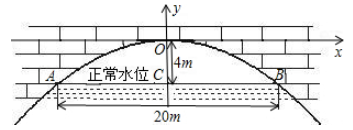
课堂练习

1. 如图所示是一个抛物线形桥拱的示意图，在所给出的平面直角坐标系中，当水位在AB位置时，水面宽度为10m，此时水面到桥拱的距离是4m，则抛物线的函数关系式为（　　）

A．y=x2         B．y=-x2

C．y=-x2    D．y=-x2

2.某市中心广场有各种音乐喷泉，其中一个喷水管喷水的最大高度为3米，此时距喷水管的水平距离为 ?/2 米，在如图所示的坐标系中，这个喷泉的函数关系式是 （　　）

A.y=-（x-）2+3

B.y=-3（x+）2+3

C.y=-12（x-）2+3

D.y=-12（x+）2+3

3.如图是一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m，在图中直角坐标系中该抛物线的解析式．

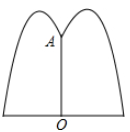
4. 如图，公园要在一个圆形的喷水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA=1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA的距离为1m处达到距水面的距离最大，高度为2.25m．若不计其它因素，那么水池的半径至少要多少米才能使喷出的水流不致落到池外？

学生独立完成，教师巡回检查，师生集体订正。

通过练习巩固本课所学，加深认识，深化提高，形成学生自己的解题技巧。

课堂小结

今天我们学习了哪些知识？

本节学习了用二次函数解决实物中抛物线形问题：

用二次函数解决抛物线形建筑问题都可以构建二次函数解析式，解此类问题的思想方法是利用  数形结合  和  函数 思想，合理建立直角坐标系，根据已知数据，运用 待定系数 求出运动轨迹（即抛物线）的解析式，再用二次的性质去分析解决问题。

学会学生体会，反思，归纳总结本节的主要收获。

通过学生亲自解决实际问题的感受与经验，总结解题各类题目的关键。